没有合适的资源?快使用搜索试试~ 我知道了~
《人工智能经典习题集与各章总结》涵盖了人工智能的基础理论和关键领域,旨在帮助学习者理解和掌握这一领域的核心概念。文档分为多个部分,包括绪论、知识与知识表示、推理等,通过习题解答的形式深化对知识的理解。 在绪论部分,介绍了人工智能的定义和发展历程。人工智能是计算机科学的分支,综合了多种学科,如计算机科学、控制论、信息论等。其发展历程分为五个阶段,从神经元网络时代到现在的海量信息处理与网络时代。这一部分还涉及了人工智能研究的基本内容,如搜索技术、知识表示、机器学习等,并提到了三大研究学派:符号主义、连接主义和行为主义,分别强调符号运算、神经元联结和行为适应。 知识与知识表示章节,重点讨论了如何表示和处理知识。以旅行问题为例,展示了产生式规则如何用来规划最短路径。此外,还介绍了不同的知识表示方法,如谓词表示法、产生式表示法、框架表示法和语义网络表示法,这些方法在解决实际问题时各有优势。 推理章节则探讨了如何运用知识进行推理。通过一系列习题,学习者可以了解如何利用推理解决实际问题,如比赛比分的语义网络表示。推理是人工智能中的关键能力,涉及逻辑推理、定理证明等。 文档中的习题解答提供了具体的应用实例,有助于学习者将理论知识转化为实践技能。例如,通过侦探破案的例子,学习者可以学习如何根据多个条件进行合逻辑的推断。 《人工智能经典习题集与各章总结》不仅覆盖了人工智能的基础理论,还通过习题和案例分析,强化了实际应用和解决问题的能力,是学习人工智能的宝贵资源。它深入浅出地讲解了人工智能的各个关键点,对于互联网行业的人工智能学习者来说,具有很高的参考价值。
资源详情
资源评论
资源推荐

1 / 57
人工智能各章小结与习题解答
第一部分 绪论
习题解答:
1.什么是人工智能?发展过程中经历了哪些阶段?
解:人工智能是计算机科学的一个重要分支,也是一门正在发展中的综合性前沿学科,它是由计算机科学、
控制论、信息论、神经生理学、哲学、语言学等多种学科相互渗透而发展起来的,目前正处于发展阶段尚
未形成完整体系。
发展过程中经历的阶段有:
第一阶段(40 年代中~50 年代末) 神经元网络时代
第二阶段(50 年代中~60 年代中) 通用方法时代
第三阶段(60 年代中~80 年代初) 知识工程时代
第四阶段(80 年代中~90 年代初) 新的神经元网络时代
第五阶段(90 年代初~现在) 海量信息处理与网络时代
2.人工智能研究的基本容是什么?
解:基本容是:搜索技术、知识表示、规划方法、机器学习、认知科学、自然语言理解与机器翻译、专家
系统与知识工程、定理证明、博弈、机器人、数据挖掘与知识发现、多 Agent 系统、复杂系统、足球机器
人、人机交互技术等。
3.人工智能主要有哪几大研究学派?
解:(1)符号主义学派:由心理学途径产生,符号主义认为人工智能起源于数理逻辑,人 类认识(智
能)的基本元素是符号,而智能行为则是符号运算的结果。
(2)连接主义学派:由生理学途径产生,连接主义又称为仿生学派,认为人工智能的基本元素是神经
元,智能产生于大量神经元的并行分布式联结之中,而智能行为则是联结计算的结果。
(3)行为主义学派:由生物演化途径产生,行为主义认为人工智能起源于控制论,提出智能取决于感
知和行为,取决于对外界复杂环境的适应,而不是表示和推理。
4.人工智能有哪些主要的研究领域?
解:(1)问题求解
(2)逻辑推理与定理证明
(3)自然语言理解
(4)自动程序设计
(5)专家系统
(6)机器学习
(7)神经网络
(8)机器人学
(9)模式识别
(10)机器视觉
(11)智能控制
(12)智能检索
(13)智能调度与指挥
(14)分布式人工智能与Agent
(15)计算智能与进化计算
2 / 57
(16)数据挖掘与知识发现
(17)人工生命
(18)系统与语言工具
第 2 部分 知识与知识表示
本章小结:
习题解答:
1 设有如下问题:
(1)有五个相互可直达且距离已知的城市 A、B、C、D、E,如图所示;
(2)某人从 A 地出发,去其它四个城市各参观一次后回到 A;
(3)找一条最短的旅行路线
请用产生式规则表示旅行过程。
解:①综合数据库(x)
(x)中 x 可以是一个字母,也可以是一个字符串。
②初始状态(A)
③目标状态(Ax1x2x3x4A)
④规则集:
r1: IF L(S)=5 THEN GOTO(A)
r2: IF L(S)<5 THEN GOTO(B)
r3: IF L(S)<5 THEN GOTO(C)
r4: IF L(S)<5 THEN GOTO(D)
r5: IF L(S)<5 THEN GOTO(E)
其中 L(S)为走过的城市数,GOTO(x)为走向城市 x
⑤路线如下图所示:
知识表示
谓词表示法
产生式表示法
框架表示法
语义网络表示法
框架通常由指定事物各个方面的
槽组成,每个槽拥有若干个侧面,
而每个侧面又可拥有若干个值。
语义网络由节点和弧线或链线组成,
节点用于表示物体、概念和状态,弧
线用于表示节点间的关系。
产生式系统由 3 个基本部分组成:规
则库、综合数据库、控制系统。
首先定义谓词,指出每个谓词的确切
含义,然后再用连接词把有关的谓词
连接起来,形成一个谓词公式表达一
个完整的意义。
3 / 57
最短旅行路线为:A->C->D->E->B->A
总距离为 5+6+8+10+7=36
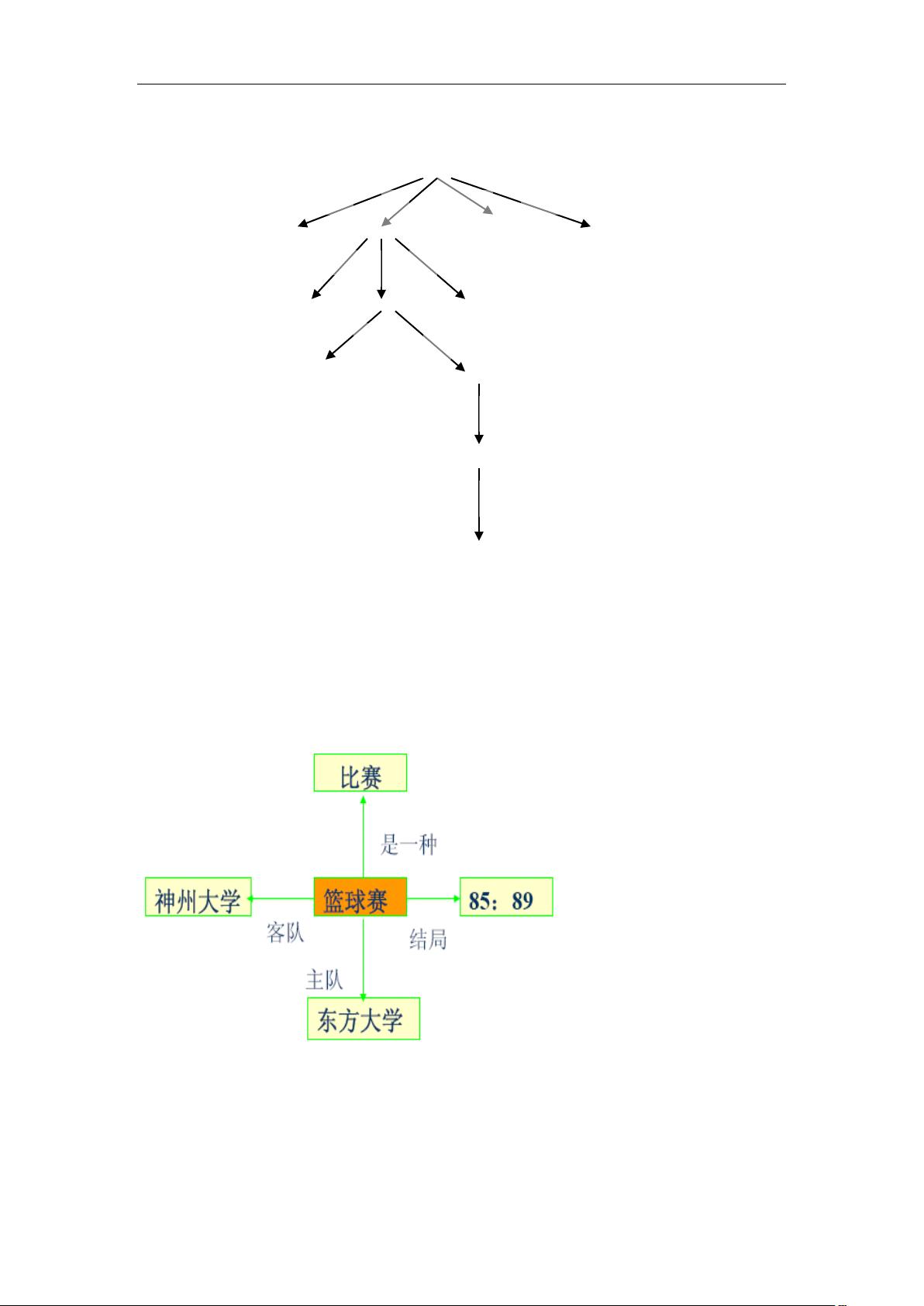
2 神州大学和大学两校篮球队在大学进行一场比赛,结局的比分是 85:89,用语义网络表示。
第 3 部分 推理
本章小结:
( A )
( AB )
( AC )
( AD )
( AE )
( A CB)
( A CD)
( ACE )
( A CDB)
( ACDE )
( ACDEB )
( ACDEBA)
7
5
10
10
7
6
9
10
8
10
7
起始
目标
4 / 57
习题解答:
1 某被盗,公安局派出五个侦察员去调查。研究案情时,侦察员 A 说“与钱中至少有一人作案”;侦察员 B
说“钱与中至少有一人作案”;侦察员 C 说“与中至少有一人作案”;侦察员 D 说“与中至少有一人与此案无
关”;侦察员 E 说“钱与中至少有一人与此案无关”。如果这五个侦察员的话都是可信的,试用归结演绎推理
求出谁是盗窃犯。
解:第一步:将 5 位侦察员的话表示成谓词公式,为此先定义谓词。
设谓词 P(x)表示是作案者,所以根据题意:
A: P(zhao) ∨ P(qian) B: P(qian) ∨ P(sun)
C: P(sun) ∨ P(li) D: ﹁P(zhao) ∨ ﹁P(sun)
E: ﹁P(qian) ∨ ﹁P(li)
以上每个侦察员的话都是一个子句。
第二步:将待求解的问题表示成谓词。设 y 是盗窃犯,则问题的谓词公式为 P(y),将其否定并与
ANSWER(y)做析取:
﹁P(y) ∨ ANSWER(y)
第三步:求前提条件与﹁P(y) ∨ ANSWER(y)的子句集,并将各子句列表如下:
(1) P(zhao) ∨ P(qian)
(2) P(qian) ∨ P(sun)
(3) P(sun) ∨ P(li)
(4) ﹁P(zhao) ∨ ﹁P(sun)
(5) ﹁P(qian) ∨ ﹁P(li)
(6) ﹁P(y) ∨ ANSWER(y)
第四步:应用归结原理进行推理。
(7) P(qian) ∨ ﹁P(sun) (1)与(4)归结
(8) P(zhao) ∨ ﹁P(li) (1)与(5)归结
(9) P(qian) ∨ ﹁P(zhao) (2)与(4)归结
推理
经典逻辑推理
不确定与非单调推理
归结演绎推理
与/或形演绎推理
自然演绎推理

5 / 57
(10) P(sun) ∨﹁P(li) (2)与(5)归结
(11) ﹁P(zhao) ∨ P(li) (3)与(4)归结
(12) P(sun) ∨﹁P(qian) (3)与(5)归结
(13) P(qian) (2)与(7)归结
(14) P(sun) (2)与(12)归结
(15) ANSWER(qian) (6)与(13)归结,σ={qian/y}
(16) ANSWER(sun) (6)与(14)归结, σ={sun/y}
所以,本题的盗窃犯是两个人:钱和。
2 任何兄弟都有同一个父亲,John 和 Peter 是兄弟,且 John 的父亲是 David,问 Peter 的父亲是谁?
解:第一步:将已知条件用谓词公式表示出来,并化成子句集。那么,要先定义谓词。
(1) 定义谓词:
设 Father(x,y)表示 x 是 y 的父亲。
设 Brother(x,y)表示 x 和 y 是兄弟。
(2) 将已知事实用谓词公式表示出来:
F1: 任何兄弟都有同一个父亲。
( x)( y)( z)( Brother(x,y)∧Father(z,x)→Father(z,y))
F2: John 和 Peter 是兄弟。
Brother(John, Peter)
F3: John 的父亲是 David。
Father(David, John)
(3) 将它们化成子句集,得
S1={﹁Brother(x,y)∨﹁Father(z,x)∨Father(z,y), Brother(John, Peter), Father(David, John)}
第二步:把问题用谓词公式表示出来,并将其否定与谓词 ANSWER 做析取。
设 Peter 的父亲是 u,则有:Father(u, Peter)
将其否定与 ANSWER 做析取,得
G: ﹁Father(u, Peter) ∨ ANSWER(u)
第三步:将上述公式 G 化为子句集 S2,并将 S1 和 S2 合并到 S。
S2={﹁Father(u, Peter) ∨ ANSWER(u)}
S=S1∪S2
将 S 中各子句列出如下:
(1)﹁Brother(x,y)∨﹁Father(z,x)∨Father(z,y)
(2)Brother(John, Peter)
(3)Father(David, John)
(4)﹁Father(u, Peter) ∨ ANSWER(u)
第四步:应用归结原理进行归结。
(5)﹁Brother(John,y) ∨ Father(David,y)
(1)与(3)归结,σ={ David/z, John/x}
(6)﹁Brother(John, Peter) ∨ ANSWER(David)
(4)与(5)归结,σ={ David/u, Peter/y}
�
�
�
剩余56页未读,继续阅读
智慧安全方案
- 粉丝: 3837
- 资源: 59万+
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- 基于java+ssm+mysql的校友录系统开题报告.doc
- 基于java+ssm+mysql的校园心理健康网站开题报告.doc
- 基于Matlab的2DPSK调制解调系统仿真全部资料+详细文档.zip
- 基于MATLAB编程环境的行人检测系统,全部资料+详细文档.zip
- 基于matlab-cfs-模板匹配的车牌识别全部资料+详细文档.zip
- 基于matlab的激光扩束系统设计全部资料+详细文档.zip
- 基于matlab的线性模型摄像机定标全部资料+详细文档.zip
- 基于matlab的少帅下飞机动画演示全部资料+详细文档.zip
- 基于matlab的一些算法验证和仿真全部资料+详细文档.zip
- python入门-13.A-B problem-暴力解决不了问题~.py
- python入门-14.生日-happy bir…….py
- Python入门经典PDF
- python入门-15.平台-这不是是男人就下100层?.py
- 焊接地轨机器人模组sw18全套技术资料100%好用.zip
- 中国高程标准地图-附带全球shp+全国行政shp+南海诸岛shp+全国高程Tif+标准成图mxd文件
- http协议课程设计PDF
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功
评论0