网络授课-《零障碍中考-数学》-第13课(1).docx
2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
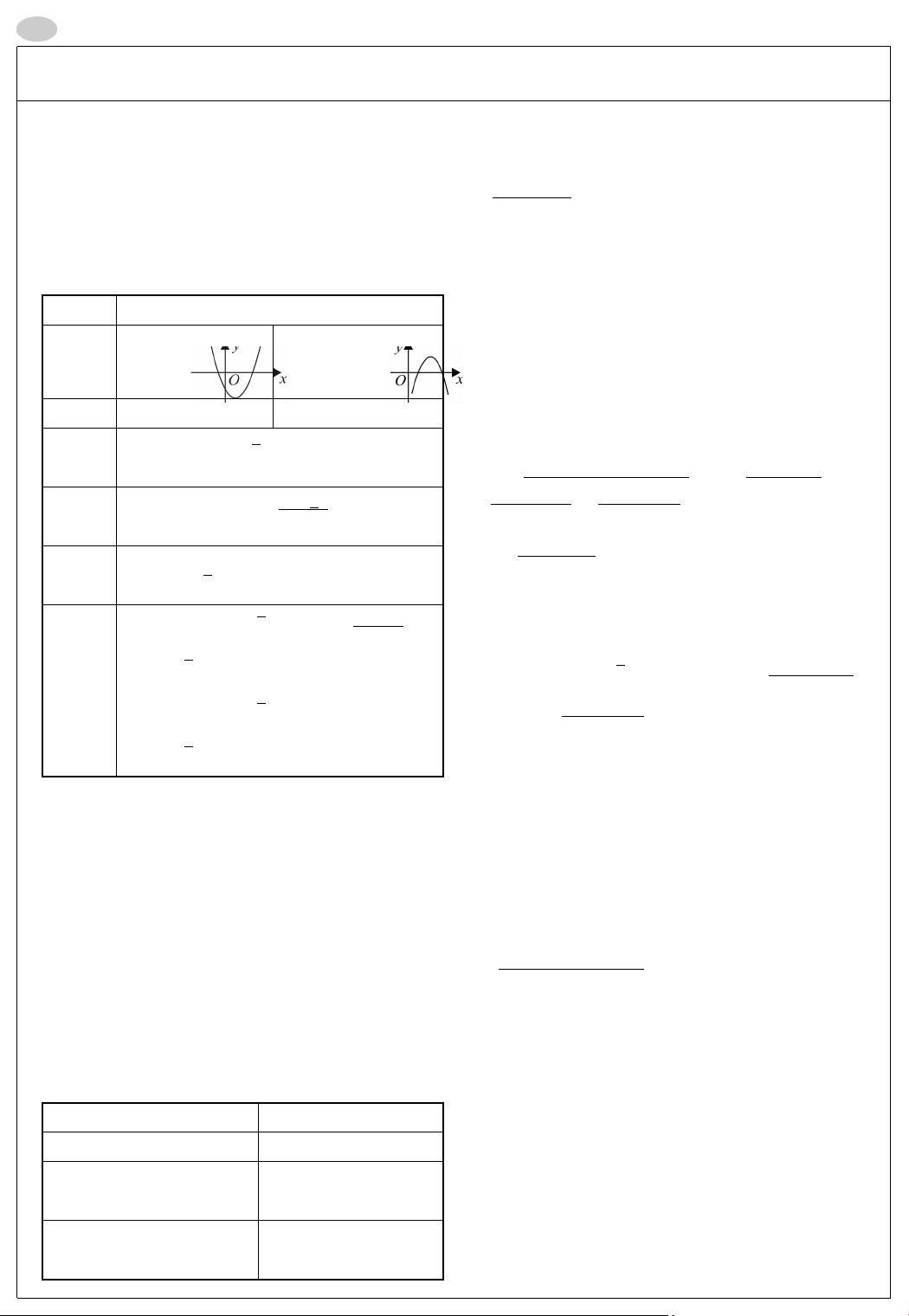
【网络授课-《零障碍中考-数学》-第13课(1)】是一份针对初中生准备中考数学复习的课程资料,主要讲解了二次函数的相关知识。在本课中,我们将深入理解二次函数的概念、图像性质以及平移规律。 **二次函数的概念**是课程的核心。二次函数的标准形式为 \( y = ax^2 + bx + c \),其中 \( a \neq 0 \),\( a, b, c \) 是常数。对于给定的函数 \( y = (m-1)x^2 + x \),如果它是二次函数,则 \( m \) 必须满足 \( m \neq 1 \)。 **二次函数的图像及性质**是学习的重点。例如,函数 \( y = 3(x-1)^2 + 2 \) 的开口向上,顶点坐标为 (1, 2),对称轴为直线 \( x=1 \)。当 \( x < 1 \) 时,随着 \( x \) 的增大,\( y \) 增大。对于函数 \( y = -x^2 - 2x + 1 \),可以将其配成顶点式 \( y = a(x-h)^2 + k \),其中 \( h \) 和 \( k \) 分别表示顶点的 \( x \) 和 \( y \) 坐标。函数的最大值发生在顶点处,可以通过完成平方来确定。 **二次函数的平移规律**阐述了如何通过改变函数表达式中的 \( h \) 和 \( k \) 参数来移动图像。例如,函数 \( y = 2x^2 \) 向右平移1个单位,向下平移3个单位后的解析式为 \( y = 2(x-1)^2 - 3 \)。 **待定系数法求二次函数解析式**是解决实际问题的一种方法。已知抛物线的顶点和另一个点的坐标,可以确定函数的具体形式。例如,一个抛物线顶点为 (1, 2),过点 (2, 3),其解析式可以通过待定系数法求得。 **二次函数的图像表达式和性质**包括开口方向(由 \( a \) 的正负决定),顶点坐标(\( -\frac{b}{2a}, \frac{4ac-b^2}{4a} \)),对称轴(直线 \( x=-\frac{b}{2a} \)),以及函数的增减性。当 \( a > 0 \) 时,函数在对称轴左侧递减,右侧递增;反之,当 \( a < 0 \) 时,函数在对称轴左侧递增,右侧递减。 通过这些知识点的学习,学生能够掌握二次函数的基本特征,这对于解决中考数学中涉及二次函数的问题至关重要。同时,了解平移规则和待定系数法将有助于解决实际应用中的函数模型。

- 粉丝: 3836
- 资源: 59万+
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- SQL语言详细教程:从基础到高级全面解析及实际应用
- 仓库管理系统源代码全套技术资料.zip
- 计算机二级考试详细试题整理及备考建议
- 全国大学生电子设计竞赛(电赛)历年试题及备考指南
- zigbee CC2530网关+4节点无线通讯实现温湿度、光敏、LED、继电器等传感节点数据的采集上传,网关通过ESP8266上传远程服务器及下发控制.zip
- 云餐厅APP项目源代码全套技术资料.zip
- vscode 翻译插件开发,选中要翻译的单词,使用快捷键Ctrl+Shift+T查看翻译
- mrdoc-alpine0.9.2
- ACMNOICSP比赛经验分享:从知识储备到团队协作的全面指南
- 云餐厅项目源代码全套技术资料.zip
- 基于STM32的数字闹钟系统的仿真和程序
- 混合信号设计中DEF文件创建流程
- 美国大学生数学建模竞赛(美赛)详细教程:从组队到赛后总结全攻略
- 病媒生物孳生地调查和治理工作方案.docx
- 保姆的工作标准.docx
- 病媒生物防制指南.docx


 信息提交成功
信息提交成功