信号与系统教学课件：4-1 Continues spectrum and CTFT.ppt

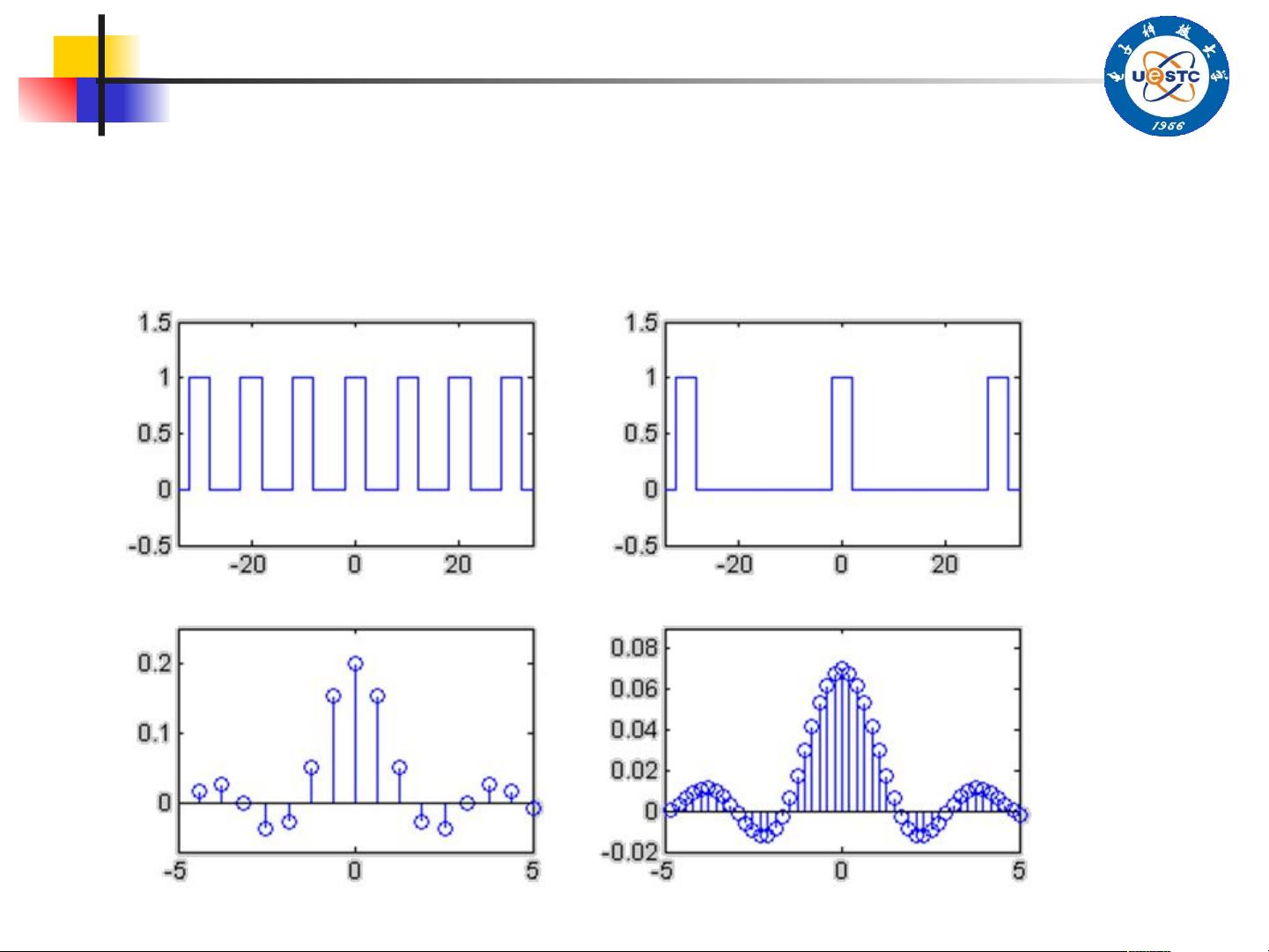
信号与系统教学课件：4-1 Continues spectrum and CTFT 本节课件主要讲述信号与系统中连续谱和连续傅里叶变换（CTFT）的知识点。 1. 连续傅里叶变换（CTFT）的定义： CTFT 是一种将时域信号转换为频域信号的数学工具。其定义为： X(ω) = ∫[−∞+∞] x(t)e^{-jωt}dt 其中，x(t) 是时域信号，X(ω) 是频域信号，ω 是频率。 2. 连续傅里叶变换的性质： CTFT 具有以下性质： * 线性：CTFT 是一个线性变换，即对于两个信号 x1(t) 和 x2(t)，有： X1(ω) + X2(ω) = CTFT{x1(t) + x2(t)} * 时域平移：CTFT 对时域信号的平移不变，即： CTFT{x(t - τ)} = X(ω)e^{-jωτ} * 频域平移：CTFT 对频域信号的平移不变，即： CTFT{x(t)e^{jω0t}} = X(ω - ω0) 3. 连续傅里叶变换的收敛条件： CTFT 的收敛条件是 Dirichlet 条件，即： * 在任何有限区域内，信号只有有限个极值点。 * 在任何有限区域内，信号只有有限个阶跃点。 * 信号是绝对可积的。 4. CTFT 的对偶性： CTFT 具有对偶性，即： X(ω) ⇌ x(t) 这意味着，如果我们知道信号的 CTFT， 就可以通过对偶性来获得时域信号。 5. 基本变换对： CTFT 有一些基本变换对，例如： * δ(t) ⇌ 1 * 1 ⇌ 2πδ(ω) * e^{jω0t} ⇌ 2πδ(ω - ω0) 这些变换对可以帮助我们快速地计算 CTFT。 6. 周期信号在 CTFT 中的表示： 对于周期信号 x(t)，其 CTFT 可以表示为： X(ω) = ∑[k=-∞+∞] X[k]δ(ω - kω0) 其中，X[k] 是傅里叶系数，ω0 是基本频率。 7. 脉冲列在 CTFT 中的表示： 对于脉冲列信号 x(t)，其 CTFT 可以表示为： X(ω) = ∑[k=-∞+∞] δ(ω - kω0) 这意味着，脉冲列信号的 CTFT 是一个脉冲列。 本节课件主要讲述了 CTFT 的定义、性质、收敛条件、对偶性、基本变换对、周期信号和脉冲列在 CTFT 中的表示等知识点。