在机械工程领域中,准确表达物体的三维形态在二维平面上是一项基础而又重要的技能。机械制图课件《第2章 点的投影》深入讲解了点在不同投影系统中的投影原理和特性,为我们理解三维物体在二维图纸上的表现方式打下了坚实的理论基础。通过本章内容的学习,我们可以掌握如何利用投影原理来完整地表达空间中的点,进而为后续章节对线和面的投影分析奠定基础。
我们必须了解点在单一投影面上的投影概念。在此情况下,点在投影面上的投影仅能表示其与该投影面的相对位置,而无法完全确定点在三维空间中的实际位置。例如,点A在投影面P上的投影点a',只能说明点A与投影面P垂直的距离,但无法反映点A的其他两个坐标值。这种单一投影的信息是不完整的,因此我们需要考虑更复杂的投影系统来获取更全面的数据。
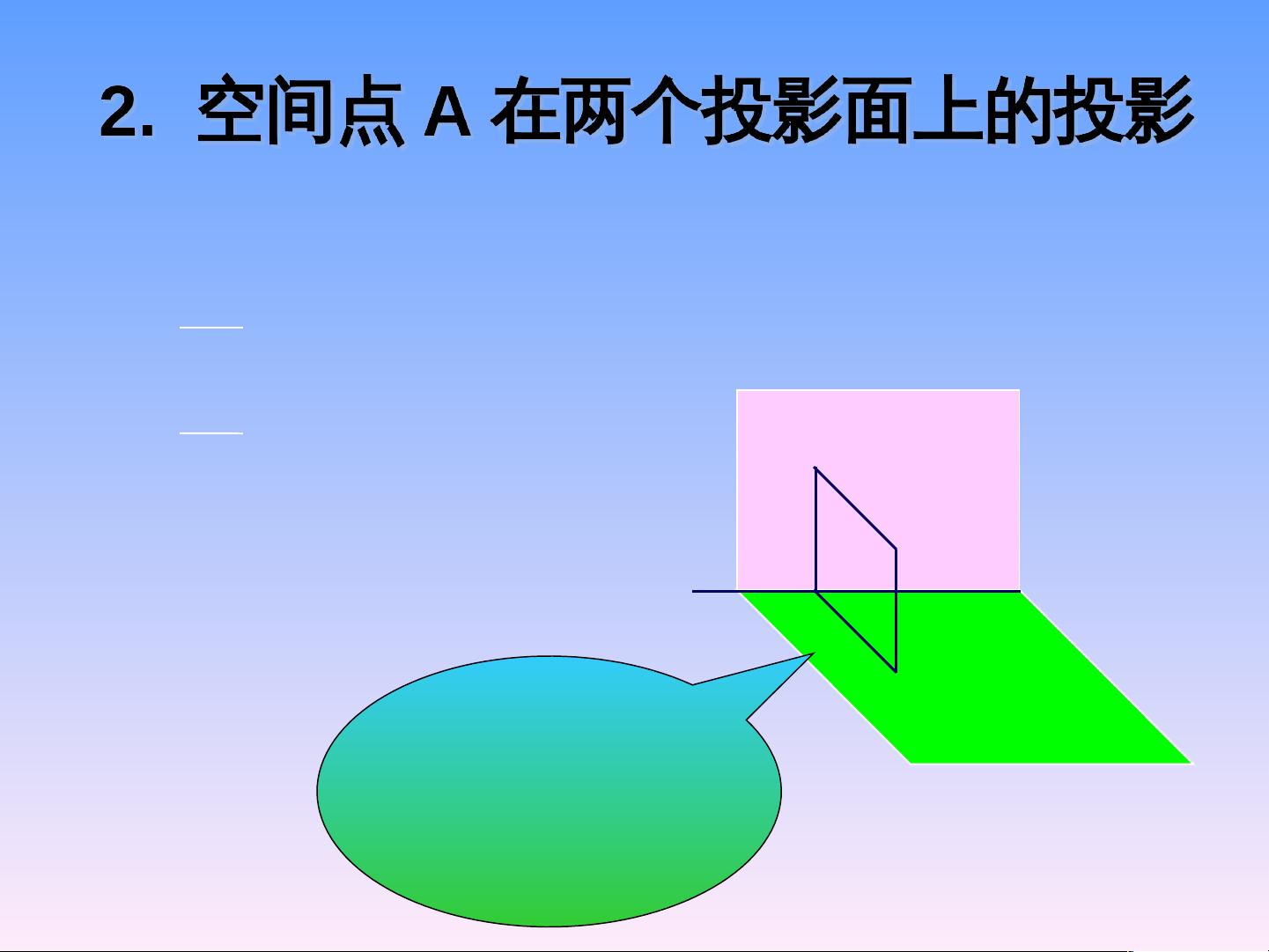
为了进一步确定点在空间中的位置,我们需要借助两投影面体系,即正面投影面V和水平投影面H。在两投影面体系中,点A在V面和H面上的投影点a'和a,能够提供两个坐标信息。这种体系遵循特定的投影规律:点A在V面的投影点a'垂直于OX轴,且点A到V面的距离等于点A的坐标值中Z轴的数值;点A在H面的投影点a到V面的距离等于点A的Y轴坐标值,到H面的距离等于X轴坐标值。尽管两面投影可以提供两点坐标信息,但若要确定点A在空间中的完整位置,仍需更多信息。
进一步地,三投影面体系的引入为点的定位提供了完整的解决方案。该体系除了V面和H面外,还加入了侧面投影面W。在此体系下,点A在三个投影面V、H、W上的投影点a'、a、a''可以完整地反映点A的空间位置。当将这三个投影面展开在同一平面上时,我们可以通过分析各投影之间的相互关系来确定点A的坐标。例如,通过点A的坐标(40,20,30),我们可以计算出其在三个投影面上的投影位置。
除此之外,点的三面投影与其在直角坐标系中的关系是相互转换的。当我们知道了点在某投影面上的投影点位置,就可以反向计算出该点在空间中的实际坐标位置,反之亦然。对于特殊位置的点,比如位于X、Y、Z轴上的点,其投影点具有特殊的几何特性,这些都需要我们特别记忆和理解。
在分析复杂图形时,两点的相对位置判定也是一个重要的内容。通过对两点在各个投影面上的投影进行比较,我们可以判断它们之间的前后、左右、上下关系。如果在某投影面上两点的投影重合,那么这两点在此投影面上被称为重影点。这是分析和理解工程图纸中复杂图形的关键知识点。
通过对点的投影理论的全面学习,我们不仅能够准确地将三维物体的特征表示在二维图纸上,还能够根据图纸准确地还原物体的三维模型。这在机械设计和制造中具有极为重要的意义,因为它是后续工艺如加工、装配、检验等环节的基础。无论是手工绘制还是利用计算机辅助设计(CAD)软件,对点的投影理论的理解都至关重要。
总而言之,点的投影是机械制图中的核心内容之一,它不仅为机械工程师提供了一种表达三维空间信息的工具,还是进行工程图纸阅读和绘制的基石。通过掌握这些基础理论,我们可以更加精确和高效地进行机械设计,确保设计意图的正确传达,为高质量的产品制造打下坚实的基础。