电路课件：第八章 线性动态电路的时域.ppt

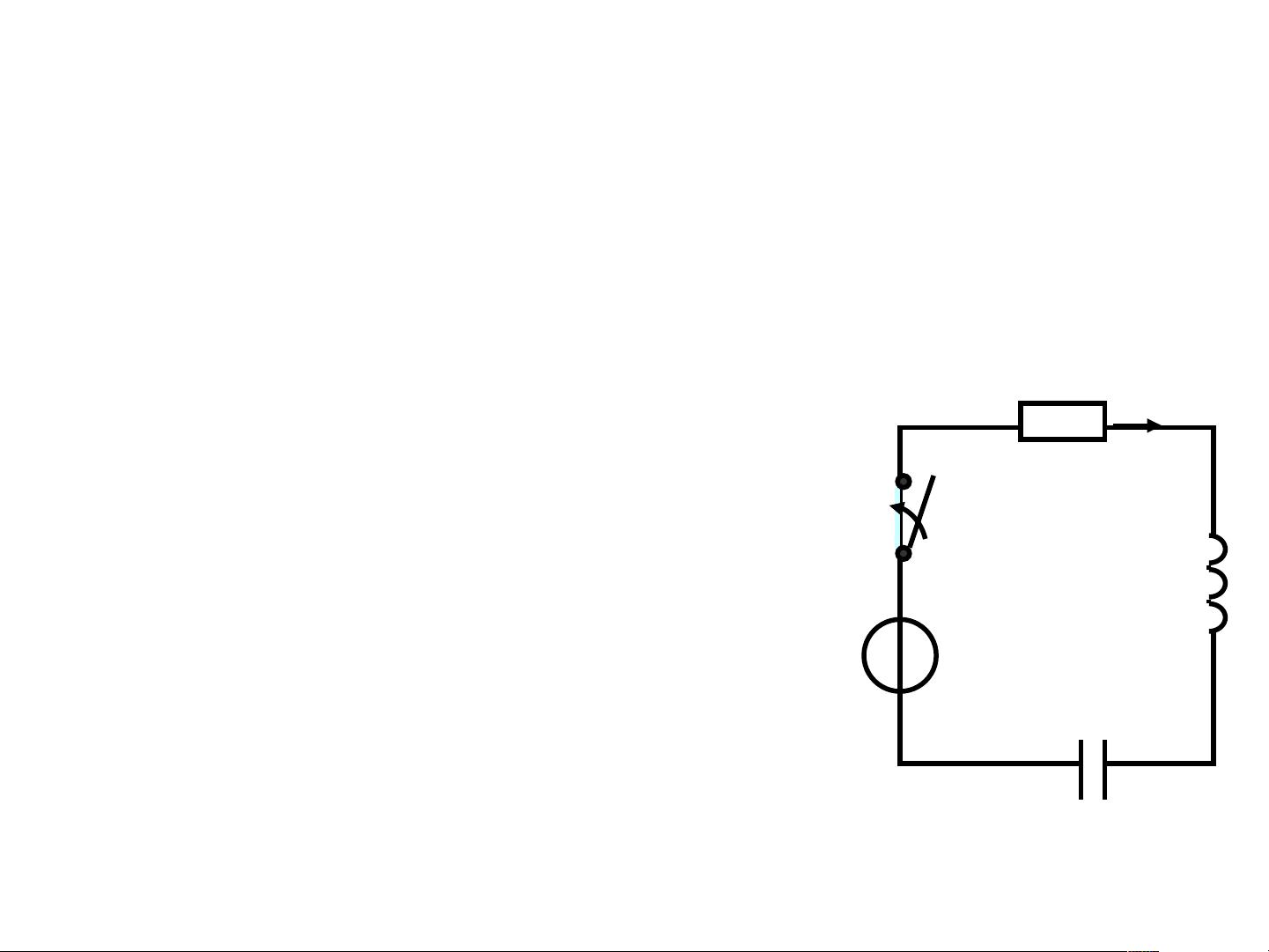
《线性动态电路的时域分析》 线性动态电路的研究是电路理论的重要组成部分，尤其在计算机和互联网领域，理解动态电路的时域行为对于电路设计和系统优化至关重要。本章主要聚焦于线性动态电路在时域中的分析，特别关注电路的稳态和暂态现象。 稳态是指当电路受到外部激励作用后，电路内部的电流和电压呈现出稳定的规律性变化。这是电路在长时间运行后达到的一种平衡状态。而暂态则是指在电路工作条件突然改变，如开关操作、故障或参数变化时，电路响应会出现短暂的非稳态波动，最终会达到新的稳态。研究暂态不仅有助于设计电力系统的保护措施，防止电路振荡，还能优化控制特性，确保系统运行的效率和稳定性。 线性动态电路的特性来源于电路中含有电容和电感这两种储能元件。电容和电感的能量变化需要时间，因此会导致电路的动态响应。电容电压和电感电流作为电路的状态变量，能反映电路的储能状态。电路微分方程的建立是基于这些状态变量，它们描述了电路中电流和电压随时间变化的规律。 在电路分析中，换路是关键事件，指的是工作条件的改变。换路瞬间分为t=0-和t=0+两个时刻，前者代表换路前趋于换路的瞬间，后者表示换路后的初始瞬间。电路的状态变量如电容电压uC(t)和电感电流iL(t)在换路前后会有不同的值，这些值就是初始状态。根据初始状态，我们可以确定电路在换路后的其他电气量，这被称为初始条件。 动态电路的微分方程可以通过基尔霍夫定律（KCL和KVL）结合欧姆定律来建立。对于线性电容，其电压和电流关系遵循电荷守恒，即电容电流的微分等于电容两端电压的变化率；对于线性电感，电流和电压的关系遵循磁链守恒，即电感电压的微分等于电感电流的变化率。换路定律指出，当电路状态改变时，电容的电荷和电压以及电感的磁链和电流在换路瞬间不会有突变，这一原则有助于我们计算出换路前后的状态值。 为了确定电路的初始值，我们需要知道换路前电路的稳态状态，即uC(0-)和iL(0-)。应用换路定律，我们可以计算出初始状态值uC(0+)和iL(0+)。在t=0+时刻，将电容视为电压源，电感视为电流源，结合独立电源的值，构建出新的电路模型，从而求解出所有电气量的初始值，完成初始条件的确定。 总结来说，线性动态电路的时域分析涉及电路的稳态和暂态行为，换路定律的应用，以及动态电路微分方程的建立。掌握这些知识对于理解和设计复杂电路系统至关重要，尤其是在计算机和互联网技术的背景下，对电路性能的精确控制和优化有着深远的影响。