线性分类器

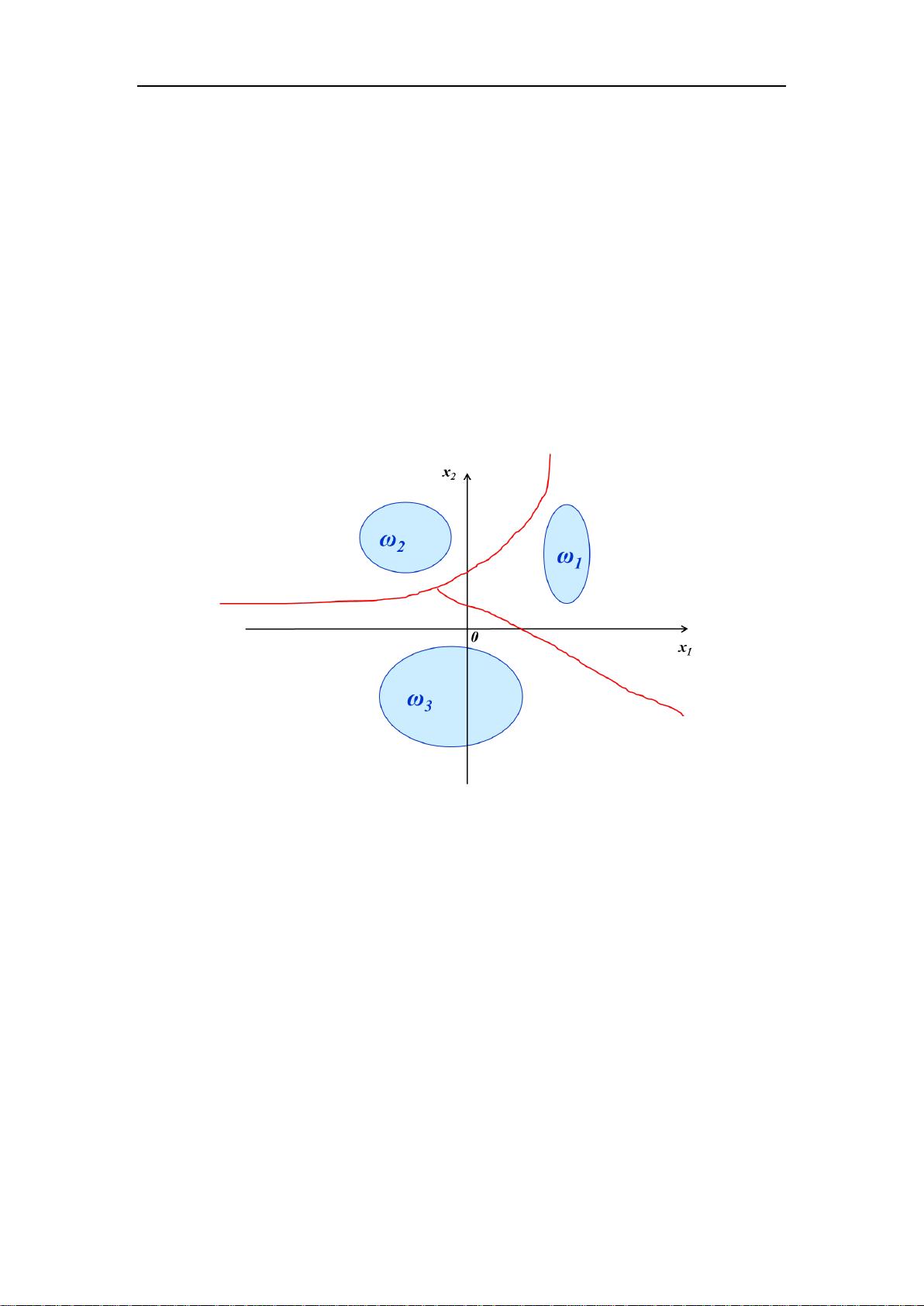
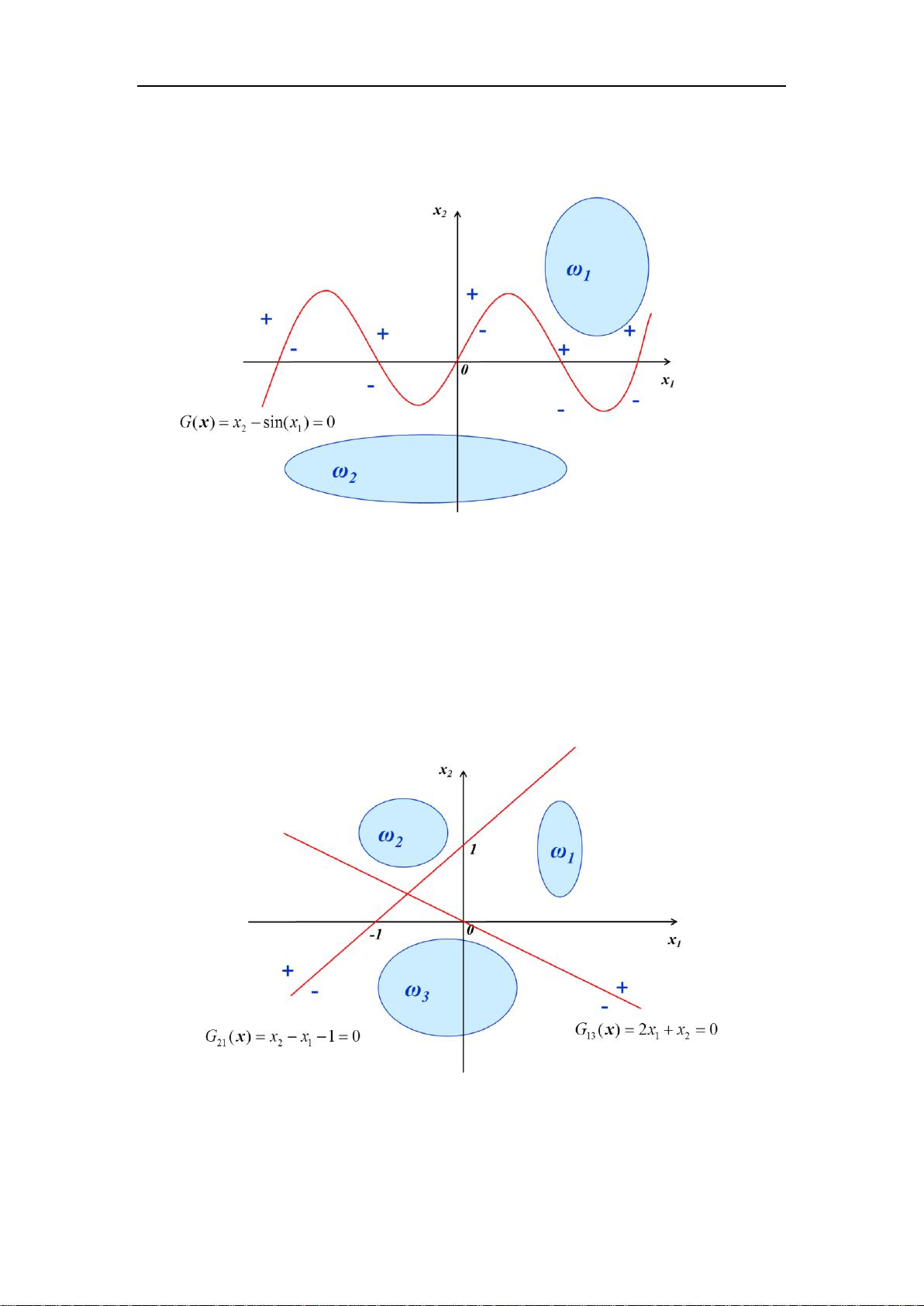
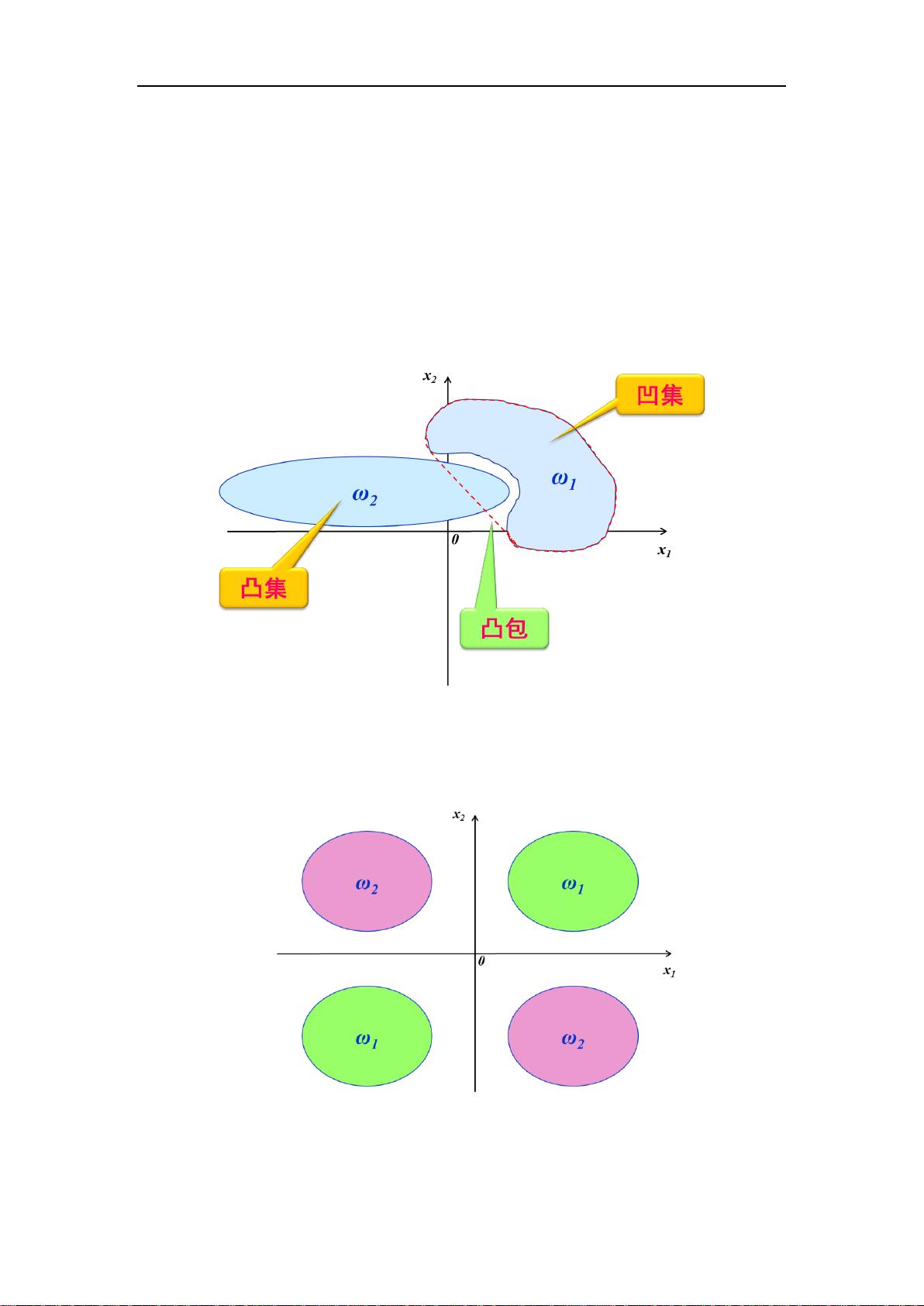
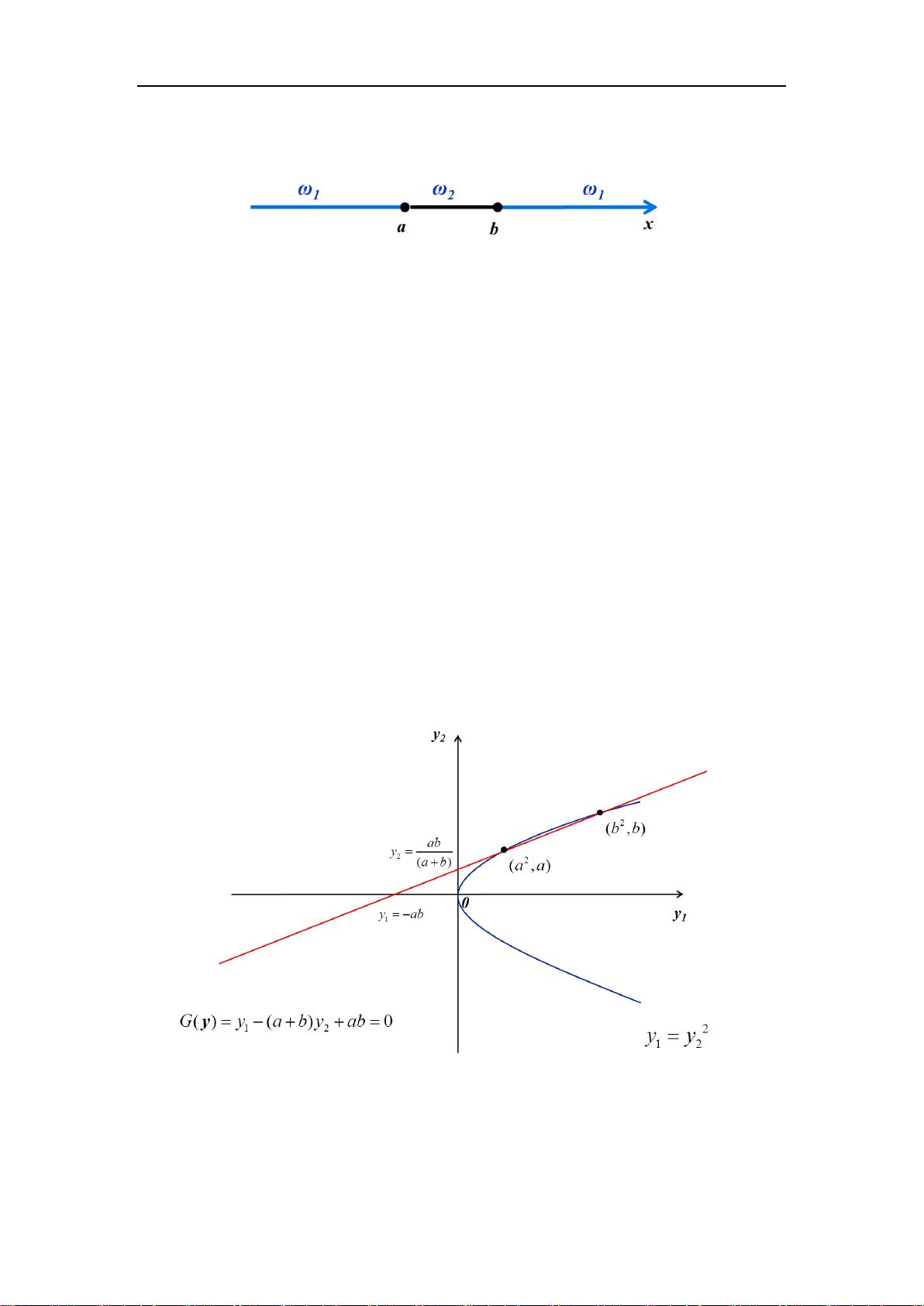
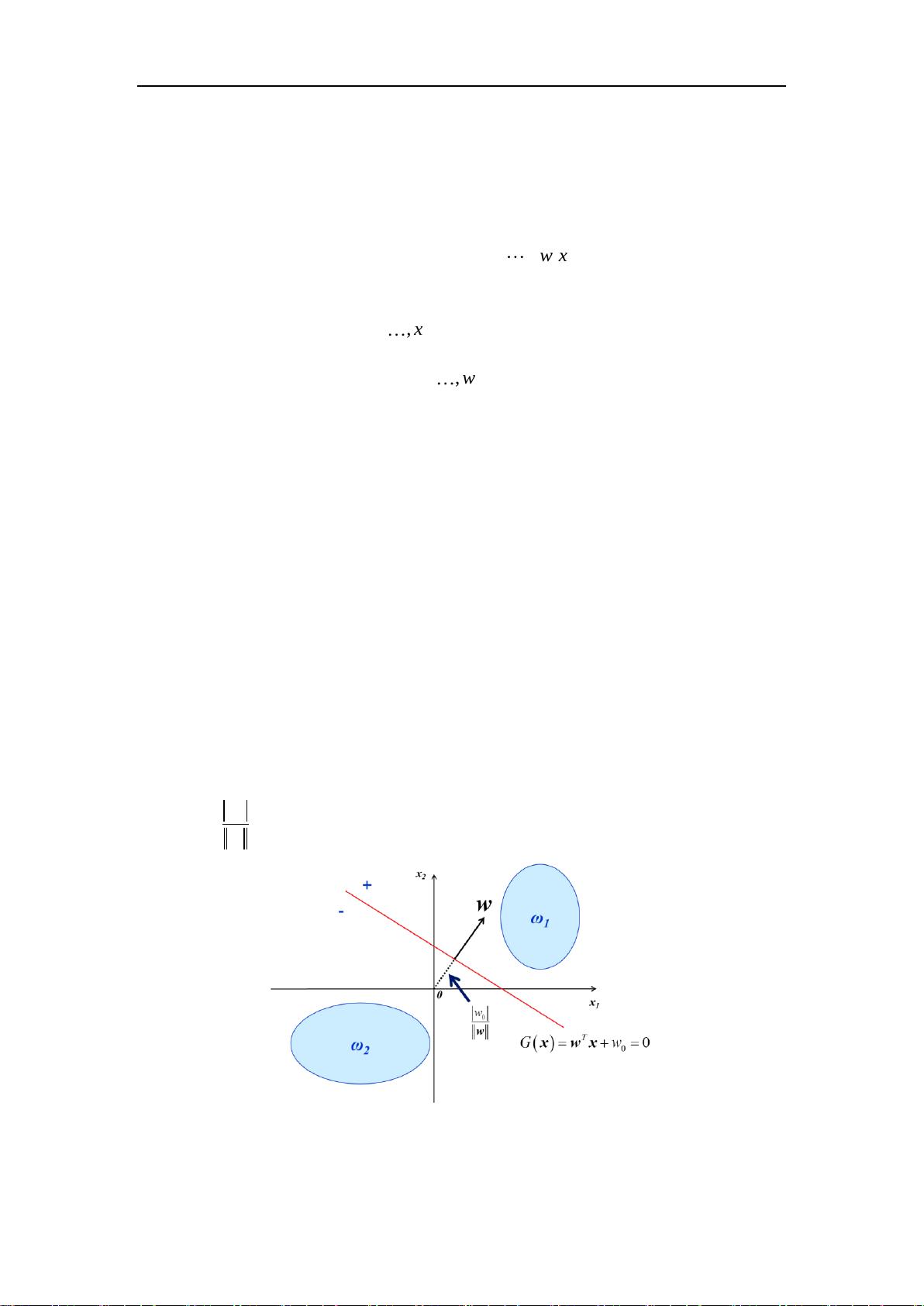
### 线性分类器详解 #### 一、判别函数与决策论方法 在模式识别领域中，**决策论方法**是一种常见的分类技术。它通过制定一定的数量规则来进行分类决策，即将待识别的模式根据其特征信息划分到不同的类别中。在决策论方法中，特征空间被划分为多个决策区域，每个区域对应一个特定的模式类。 **判别函数**是在决策论方法中用来判断待分类模式归属的关键工具。判别函数可以是线性的也可以是非线性的。当特征空间中的决策区域边界可以用线性方程表示时，这样的决策区域可以用超平面来划分。这种情况下，判别函数通常采用线性形式，这在实际应用中更为简便有效。 #### 二、线性可分性与广义线性判别函数 线性可分性是指在特征空间中是否存在一个超平面能够将不同类别的样本完全分开。当两个类别的分布范围是全连通的单一凸集且互不重叠时，它们是线性可分的。反之，则可能存在线性不可分的情况。线性不可分有以下几种情形： 1. **至少有一个类别的分布范围是凹的**，且其凸包与另一个类别的分布范围重叠。 2. **一个类别的分布范围由两个以上不连通的区域构成**，如经典的异或(XOR)问题。 对于某些线性不可分的问题，可以通过将其映射到更高维度的空间来解决。例如，在一维特征空间中无法线性分开的两个类别，可以通过引入新的特征维度，将问题转化为二维或更高维度的线性可分问题。在这个过程中，判别函数也会随之转变为广义线性判别函数。 #### 三、线性分类器设计 线性分类器主要用于处理线性可分的问题。对于两类线性可分的情形，可以构造出线性判别函数来实现分类。假设我们有两个类别ω1和ω2，特征空间中的一个模式x可以通过下面的判别函数进行分类： \[ G(x) = w^T x + w_0 \] 其中，\( w \) 是权向量，\( w_0 \) 是偏置项。对于任意一个模式 \( x \)，若 \( G(x) > 0 \)，则 \( x \) 属于类别 ω1；若 \( G(x) < 0 \)，则 \( x \) 属于类别 ω2。 #### 四、经典线性分类器模型 1. **感知器**：感知器是一种早期的线性分类器，由Rosenblatt在1958年提出。它的目标是最小化分类错误率。感知器算法通过不断调整权向量和偏置项来改善分类性能。 2. **最小均方误差(LMS)**：LMS算法是一种基于梯度下降的方法，用于最小化预测值与实际值之间的平方误差。在模式识别中，LMS可以用于构建线性分类器。 3. **支持向量机(SVM)**：SVM是一种强大的机器学习方法，旨在找到能够最大化类别间隔的最优超平面。SVM不仅适用于线性可分的情况，还可以通过核技巧处理非线性可分的问题。 #### 结论 线性分类器是模式识别中一种重要的分类方法，特别是在处理线性可分问题时非常有效。通过合理的特征选择和模型设计，线性分类器能够在很多应用场景中达到满意的分类效果。同时，对于一些非线性问题，通过特征映射等技术也能有效地将其转化为线性问题来解决。