图与网络的发展历史悠久。众所周知,图论中的几个古老的问题:哈密顿的周游世界问 题、欧拉的七桥问题,以及地图的八色问题等。而网络中的许多问题,都具有很强的实用背 景,虽然历史不是太长,但由于实用性强,所以发展很快。网络问题的第一本专著是Ford, L.R.et.al(1962)的网络流“Flows in Networkc”。有人认为该书象征着整数线性规划发展 的一个“里程碑”。不管它是否是里程碑,却给出了一大类整数规划的求解方法和研究整数 规划的新思路 网络流理论是图论中的一个重要分支,它主要关注如何在给定的网络中,通过网络的边从源点(source)到汇点(sink)传输尽可能多的流(flow)。这个概念在物流、交通、通信等众多领域中具有广泛的应用价值。网络流问题的核心包括了最大流问题、最小费用流问题以及网络的最短路问题等。 最大流问题是网络流理论中的一个基本问题,它旨在找出从源点到汇点的最大流量,即网络中可以传输的最大信息量或物质量。这个概念最早可以追溯到20世纪初期,而直到1962年,福特和富尔克森(Ford and Fulkerson)提出了一种名为“Ford-Fulkerson”方法的算法,它标志着网络流问题研究的一个重要里程碑。该算法通过不断寻找增广路径(augmenting path),即从源点到汇点的路径上还有剩余容量的路径,逐步增加流量直到找不到这样的增广路径为止。后来的算法如Edmonds-Karp算法,通过使用广度优先搜索来实现更高效的增广路径查找,使得最大流问题的求解速度得到了大幅提升。 在描述网络流算法时,我们常常使用图论中的术语。图由顶点(或节点,nodes)和边(edges)组成,边连接了不同的顶点,并且每条边都有一个定义了该边容量(capacity)的非负值,即这条边能够传输的最大流的大小。网络流问题的求解涉及到多个概念,例如流量(flow)、残余网络(residual network)和割(cut)等。流量是指给定网络中,从源点到汇点实际传输的流的大小。残余网络是基于当前流状态构建的一个虚拟网络,其中的边表示原网络中未被完全利用的容量。割是指将图分割成两部分的一组边,使得源点和汇点被分在两个不同的集合中,割的容量是指所有这些边容量的总和,最小割是指容量最小的割,它在网络流问题中有着特定的意义。 在实际操作中,最大流问题可以通过多种方法求解。除了Ford-Fulkerson方法及其改进版Edmonds-Karp算法之外,还有基于线性规划的方法,比如Dinic算法、Push-relabel算法等。这些算法各自有其特点和适用场景,比如Dinic算法能够高效地处理一些特定类型的网络流问题。 网络流问题的研究不仅限于最大流问题,还包括最小费用流问题、多源多汇问题等。最小费用流问题在最大流的基础上引入了边的单位流量传输费用,旨在寻找一种流的分配方式,使得传输费用最低。而在多源多汇问题中,源点和汇点不止一个,问题变得更加复杂,需要考虑所有源点和汇点之间的流量分配问题。 图的搜索算法是求解网络流问题的基础,其中深度优先搜索(DFS)和广度优先搜索(BFS)是最常用的两种算法。深度优先搜索在寻找增广路径时非常有效,它通过递归的方式尽可能地深入搜索。而广度优先搜索则适合寻找最短路径,它逐层地向外扩散,直到找到目标。 在我国,图与网络的研究始于20世纪五十年代末,并取得了一系列有国际影响的研究成果。例如,在物资调运问题中的图上作业法、中国邮递员问题、最小树形图问题等。这些成果展现了我国学者在这一领域的研究实力和贡献。 网络流问题的研究不仅对于理论具有重要意义,而且在实际应用中也极为广泛。无论是在计算机网络中的数据传输、交通网络的规划,还是在供应链管理和经济模型的构建中,网络流理论和算法都发挥着不可或缺的作用。随着计算能力的提升和算法的不断优化,网络流理论和相关技术将继续推动各领域的创新发展。

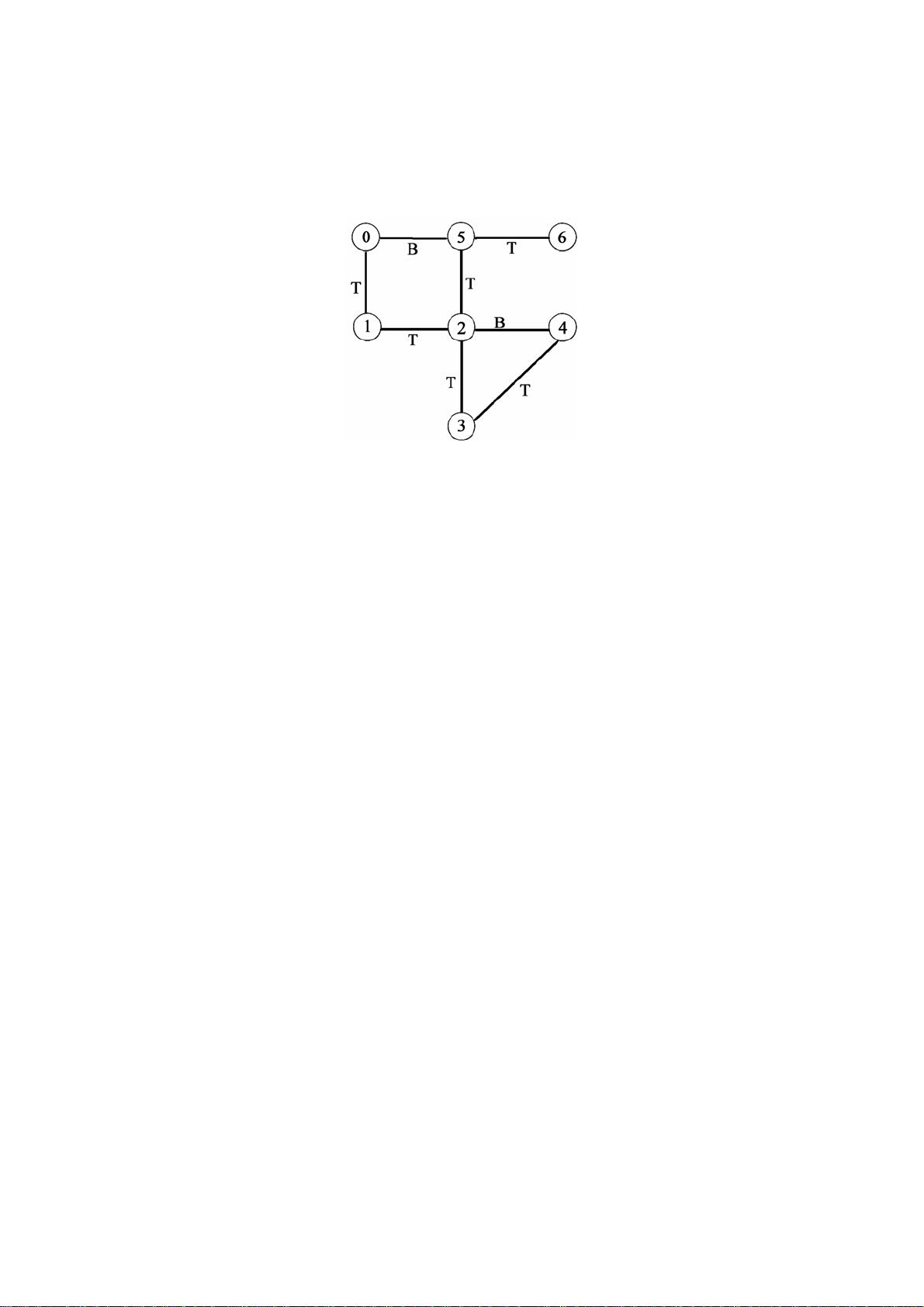
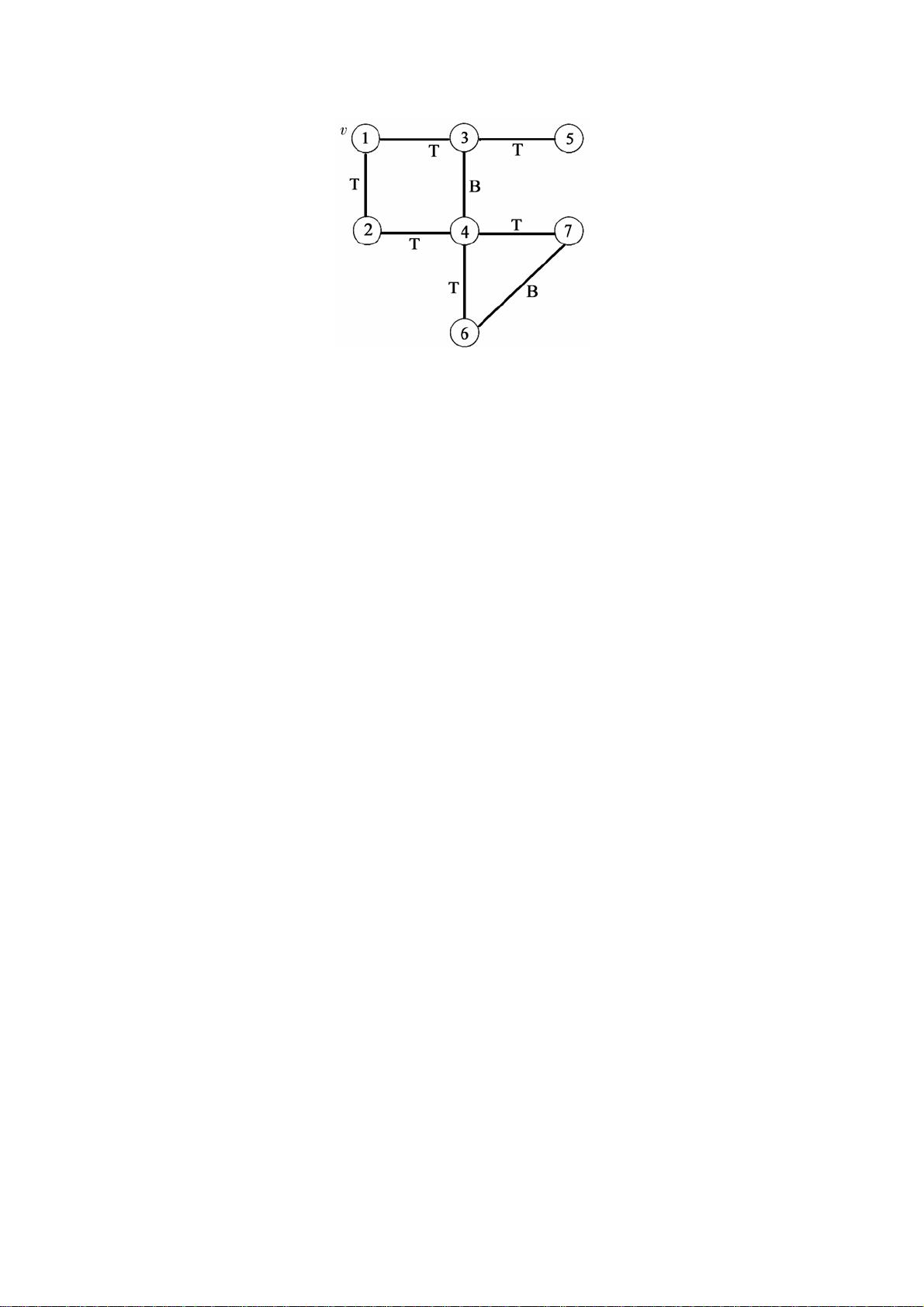


剩余38页未读,继续阅读

- 粉丝: 0
- 资源: 2
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功