·22· 计算机与信息技术 开发与应用
基于模糊Petri网的规则推理优化算法
杨蓉
(深圳大学 机电与控制工程学院,广东 深圳 518000)
摘 要 针对现有模糊 Petri 网的规则推理算法存在的不完善问题,提出并开发了优化的推理算法。该算法适用于大部
分基于规则的推理系统,正确直观的仿真从出发命题开始到目标命题的推理过程。详细阐述了模型和算法,对具体的算例进
行分析并与已有的算法进行比较突出其优点。
关键词 模糊 Petri 网;基于规则;推理;知识表示
1 引言
模糊 Petri 网(Fuzzy Petri Net,FPN)作为一种适合于描述
异步、并行、模糊数据的计算机系统模型,被广泛的应用在
基于规则的模糊推理系统中。伴随 FPN 的发展,相应模型的
顺向推理算法以及逆向推理算法也在不断发展与完善。
Looney 最早给出了只适合于简单 PN 结构的顺向推理算法
[3]
。
其后,Chen 又给出了具体且精确的 FPN 数学定义,并优化了
原有算法
[1]
。Li 等人提出了一种具有自适应能力的 FPN
[4]
,不
但可以实现知识推理,同时具有类似神经网络的自我学习能
力。
我们发现,现有的这些算法对于较简单的模型结构比较
有效,当推理系统对应的 FPN 模型具有较复杂的结构时,则
存在一定的问题,譬如:
(1)一些从始发命题到结论命题的推理路径并未充分考
虑,如文献[1]。
(2)不适合并行推理,如文献[1][3]。
(3)对于一些库所,即使在推理中得到了它们的令牌值
(Token),但在后续过程中不能被涉及到,如文献[1]。
(4)在文献[4]中,当一个变迁被允许发生后,其输入库所
全部被删除,这部分被删除掉的库所有可能包含了其它库所
的输入库所,造成整个推理无法正常进行。
因此,文本在以往研究的基础上,提出一种更具有灵活
性和适用性的基于模糊 Petri 网的顺向规则推理算法。
2 基于 Petri 网的模糊推理
一个模糊 Petri 网包含两种节点:库所(Place)和变迁
(Transition)。有向弧可以从库所指向变迁或从变迁指向库所。
在图形表示中,库所由圆形节点表示,变迁由方形节点表示。
将 FPN 应用于规则系统中,每条规则表示为一个变迁,该规
则的前提命题和结论命题则表示为该变迁的输入库所和输出
库所。每个库所都有可能包含令牌值(Token)用来描述该库所
对应的命题的可信度(Degree of Truth)。每个变迁对应一个确
信因子(Certainty Factor,CF)用来表述对应规则的确信度。
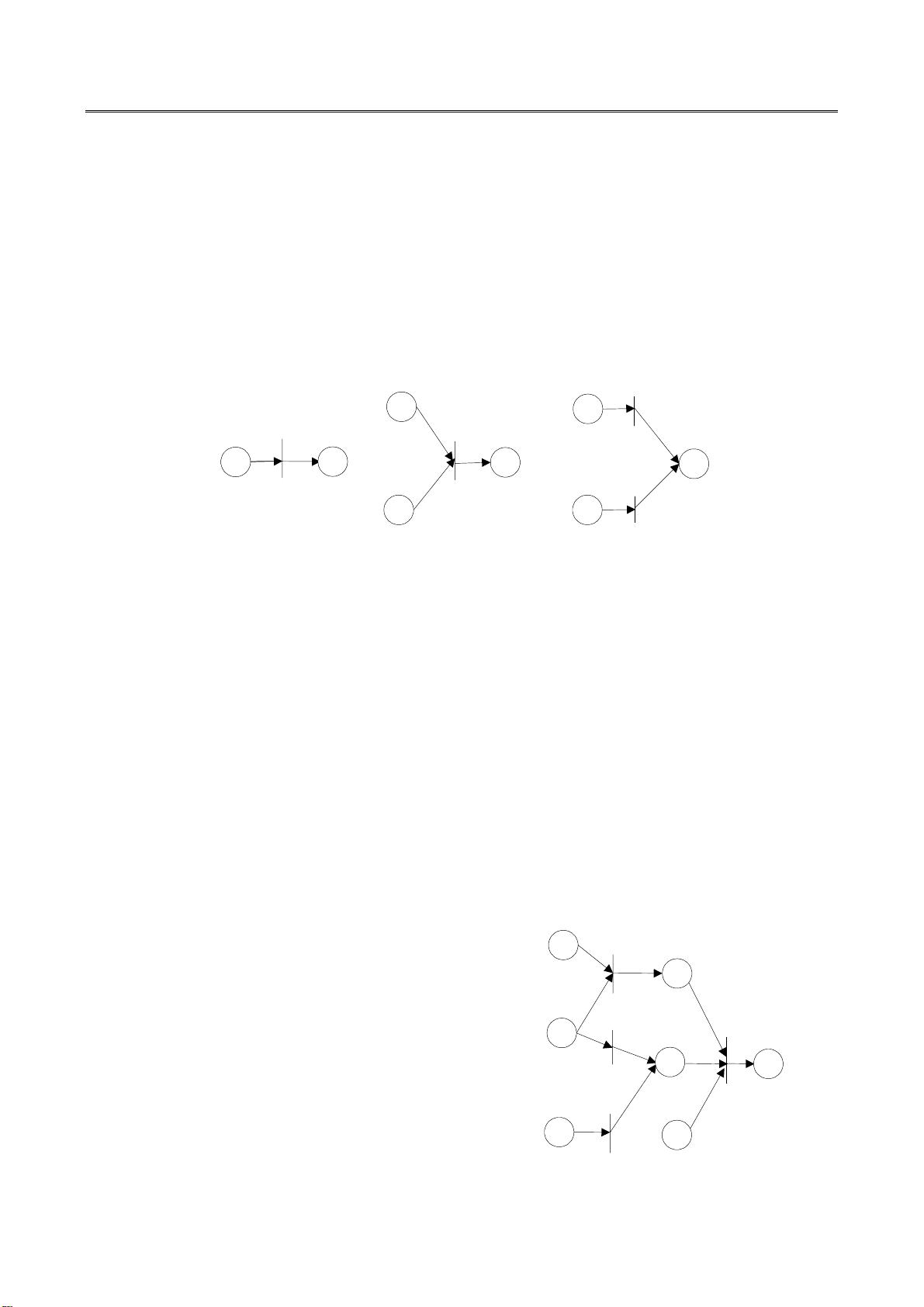
实例一:假设有如下规则:
假如 A is B,则 C is D。
该规则包含一个前提命题
BisAd :
1
和一个结论命题
DisCd :
2
,命题
21
dd , 用对应的库所
21
pp , 表示,规则用
变迁
1
t 表示,则该规则可用如图 1 的 FPN 表述。
图 1 基于实例一规则的 FPN
根据文献[1]中的定义,一个基于规则系统的 FPN 可以被
定义为一个六维量:
),,,,,(
O
P
。
其中,
},,,{
n
pppP "
21
=
为有限的库所集合,对应命题;
},,,{
n
tttT "
21
=
为有限的变迁集合,对应规则;
:IT P→
为映射变迁到其所有输入库所的输入方程;
:OT P→
为映射变迁到其所有输出库所的输出方程;
:[0,1]FT→
为映射变迁到其确信因子的方程;
:[0,1]WP→
为映射库所到其令牌指的方程。
如果一个变迁
i
t
满足条件:对于任何
)(
is
tIp ∈
,有
λ
≥)(
s
pW
,
为介于 0 和 1 之间的阈值,则该变迁将被点燃
(Fired),其输入库所的令牌值将被复制,并通过一定的点燃
机制为该变迁的输出库所产生令牌值。
例如,根据 FPN 的定义,实例一中的规则可被规范化为
),,,,,( WFOITPFPN =
1
,其中
},{
21
ppP =
,
}{
1
tT =
,
}{)(
11
ptI =
,
}{)(
21
ptO =
,
750
1
.)( =tF
,
90
1
.)( =pW
,
空=)(
2
pW
。若 令
50.
,
则
1
t 点燃,根据图 2 的点燃机制,可得到输出库所
2
p 的令牌
值为 0.675。
当然,实际的规则不可能像实例一中那样简单,在其命
题中有可能包含类似“与(AND)”或“或(OR)”连接符。我
0.9
1
2
t
1
CF=0.75