假设图中数据元素类型是字符型，请采用邻接矩阵或邻接表实现图的以下基本操作： （1）构造图（包括有向图、有向网、无向图、无向网）；...

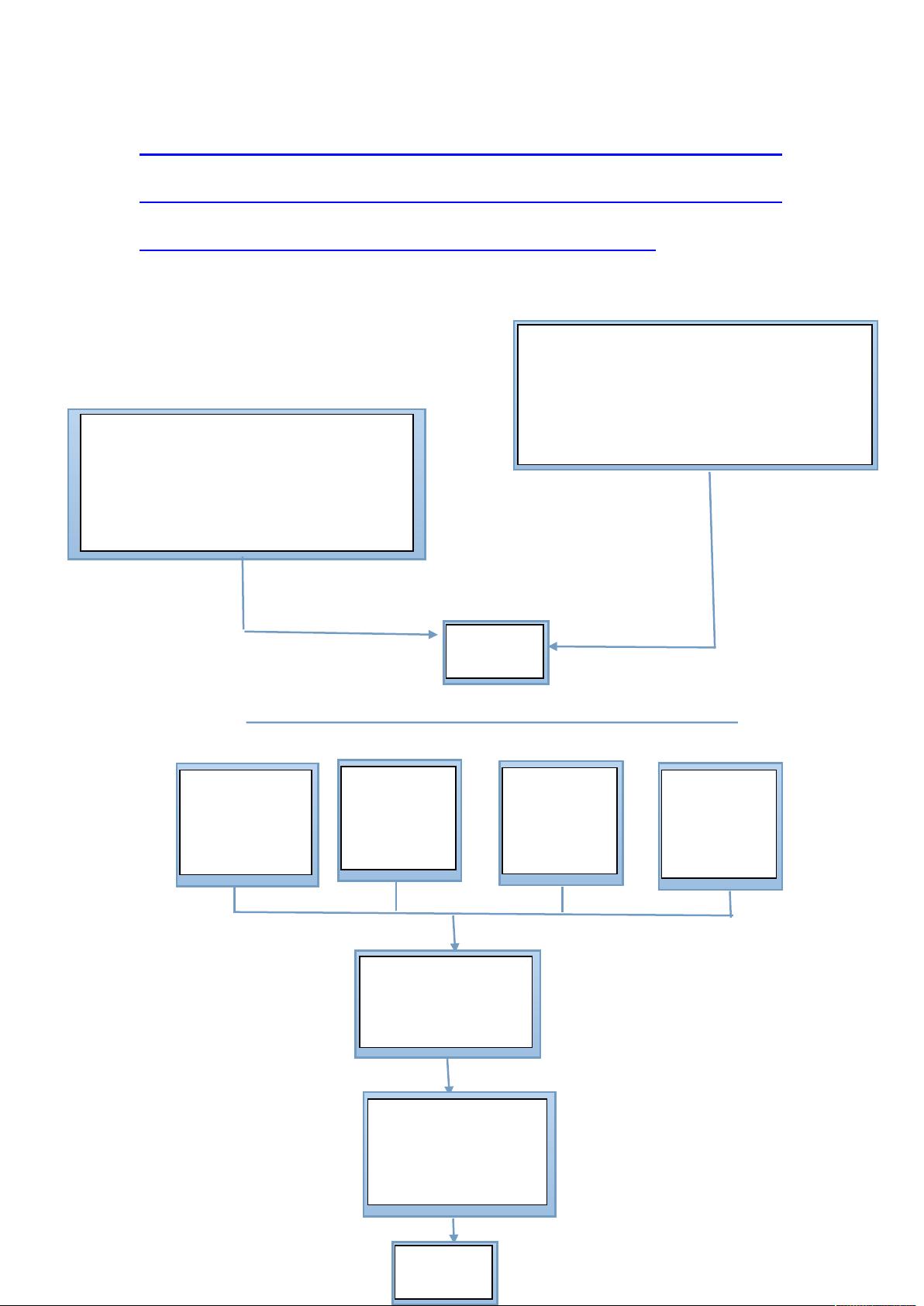
1、图和网的区别：网是带权值的图 有向和无向的区别：有向直接标出谁指向谁，无向是有向的特例，<v1,v2>有弧，说明<v2,v1>也有弧。 构图： ①　确定顶点数，弧数，是否有权值 ②　输入每个顶点，弧<弧尾，弧头>，权值 ③　若是无向，则需实现弧<v2,v1>与<v1,v2>的同置 2、图的深度优先搜索遍历类似于树的先根遍历，沿着初始顶点出发的一条路径，尽可能深入地前进，直到所有顶点被访问完；用visited[]来存储顶点的访问情况，初始时所有顶点皆为未访问FALSE，访问一个顶点之后就被标记为已访问TRUE。 在本文中，我们将探讨如何利用邻接矩阵或邻接表实现图的基本操作，特别是针对字符型数据元素的图。这包括构造有向图、有向网、无向图和无向网，以及进行深度优先遍历。我们来理解图和网之间的区别。 **图和网的区别**： 图是由顶点和连接顶点的边构成的数据结构。网则是图的一种特殊形式，它包含了带权值的边。有向图是指边具有方向，即从一个顶点指向另一个顶点，而无向图则没有明确的方向，每条边可以视为两个顶点之间的双向连接。无向图可以看作是有向图的特殊情况，其中每条有向边(v1, v2)都对应着另一条相反方向的边(v2, v1)。网与图的主要区别在于，网的边带有权值，而普通的图则可以是没有权值的。 **构造图的过程**： 1. 确定图的顶点数，即图中元素的数量。 2. 输入每个顶点及其相关的边，对于有向图，每条边表示为弧尾和弧头的组合；对于无向图，需要为每条边添加反向的边，因为无向图中任何边都是双向的。 3. 如果是带权值的网，还需要输入边的权值。 **深度优先搜索遍历**： 深度优先遍历类似于树的先根遍历，从一个起始顶点开始，沿着一条路径尽可能深地探索，直到访问完所有顶点。在遍历过程中，通常使用一个visited[]数组来记录顶点的访问状态，初始化时所有顶点都标记为未访问（FALSE），访问过一个顶点后将其标记为已访问（TRUE）。这种方法确保了每个顶点只被访问一次。 为了实现这些操作，我们需要定义一些数据结构和函数。例如，可以定义一个ArcCell结构体来存储边的信息，包括权值和附加信息。Mgraph结构体用来表示整个图，包括顶点向量、邻接矩阵和图的顶点数和边数。 在程序设计中，我们可能会有以下函数： - `Input()`：用于录入边的权值和其他信息。 - `LocateVex()`：查找指定顶点在图中的位置。 - `CreateDG()`, `CreateDN()`, `CreateUDG()`, `CreateUDN()`：分别用于构造有向图、有向网、无向图和无向网。 - `FirstAdjVex()`, `NextAdjVex()`：返回顶点的邻接顶点。 - `Print_JZ()`：打印邻接矩阵。 - `DFS()`: 从指定顶点开始进行深度优先遍历。 - `DFSTraverse()`：对整个图进行深度优先遍历。 在编程实现时，可以使用C++语言，并定义必要的头文件和常量，如访问标志数组`visited[MAX_VERTEX_NUM]`，以及表示状态和定义图的最大顶点数`MAX_VERTEX_NUM`。 通过以上描述，我们可以构建一个能够处理字符型数据元素的图，执行构造图和深度优先遍历的基本操作。这些操作对于理解和应用图论在实际问题中的解决至关重要，例如在路由算法、社交网络分析、数据挖掘等领域。