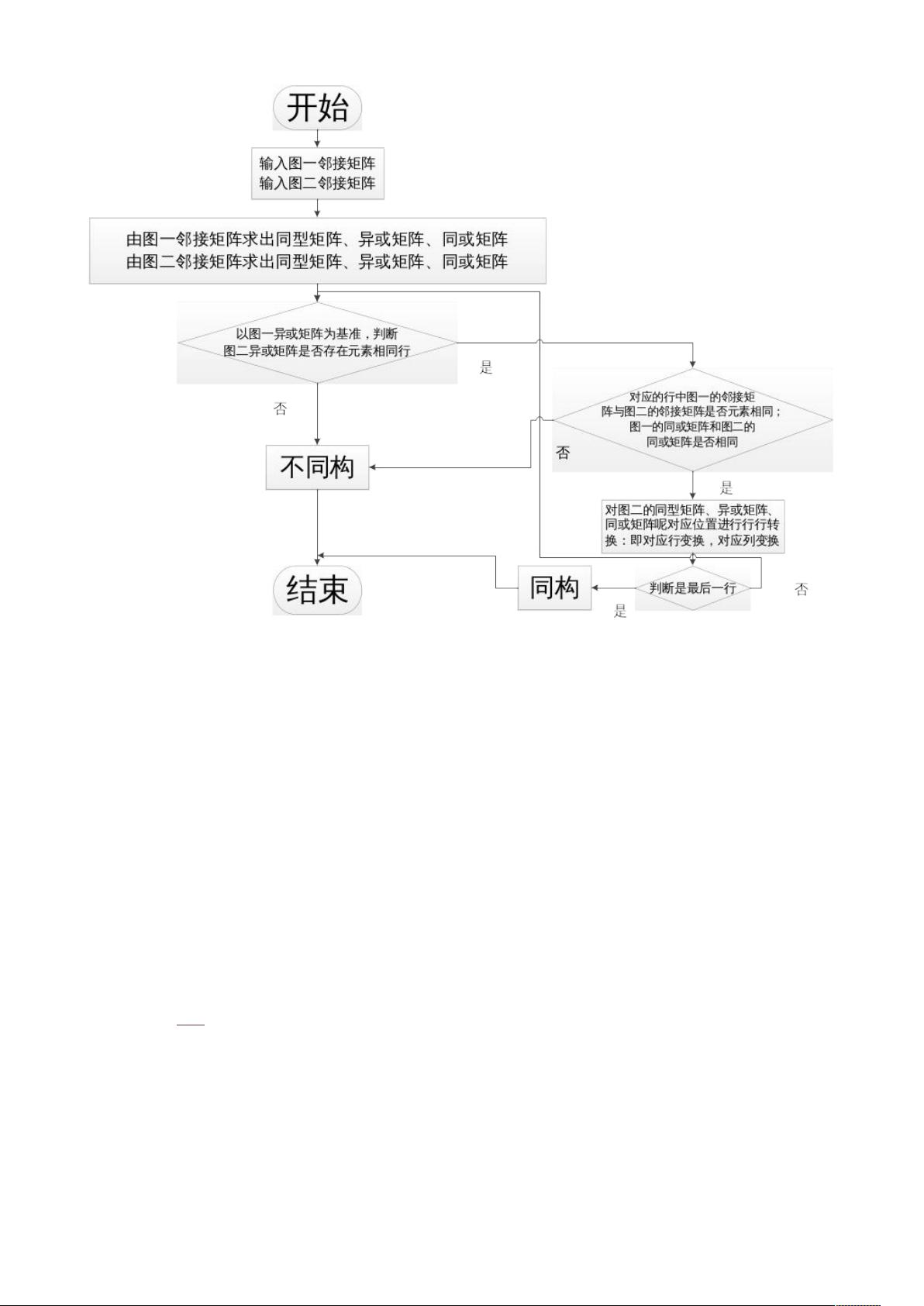
基于矩阵变换算法的图同构识别

基于矩阵变换算法的图同构识别 本资源摘要信息将对基于矩阵变换算法的图同构识别进行详细的知识点总结。 一、矩阵变换算法概述 矩阵变换算法是图同构识别的核心算法，该算法通过矩阵变换来判断两个无向图是否同构。该算法的主要思想是将图的邻接矩阵、行间同或矩阵和行间异或矩阵进行比较，以确定两个图是否同构。 二、矩阵变换算法步骤 矩阵变换算法的步骤可以概括为以下几个步骤： 1. 求出同型矩阵 AAG、AAG’。 2. 计算出行间同或矩阵 RAG、RAG’，行间异或矩阵 RXG、RXG’。 3. 以图 G=(V,E)的行间异或矩阵为参照，对 RXG 的每一行，从 RXG’搜索所有行，找到一个匹配。 4. 判断邻接矩阵 AG、AG’，行间同或矩阵中是否存在同样的匹配，若匹配存在，调整邻接矩阵 AG’、行间异或矩阵 RXG’、行间同或矩阵 RAG’对应的行和列；若不匹配，则不同构。 三、矩阵变换算法实现 矩阵变换算法的实现可以通过Java代码来实现。下面是该算法的关键代码： public static void hx(int [][]p1,int [][]p13,int [][]p14,int [][]p2,int [][]p23,int [][]p24,int n) ... 四、实验环境和任务 本实验环境使用PC机，CPU主频为2.2GHZ，内存为4GB，操作系统为Windows，编程语言为Java。实验任务是使用矩阵变换算法来判定两个无向图是否同构。 五、实验思路 实验思路是：根据定义，求出同型矩阵 AAG、AAG’。然后，计算出行间同或矩阵 RAG、RAG’，行间异或矩阵 RXG、RXG’。接着，以图 G=(V,E)的行间异或矩阵为参照，对 RXG 的每一行，从 RXG’搜索所有行，找到一个匹配。判断邻接矩阵 AG、AG’，行间同或矩阵中是否存在同样的匹配，若匹配存在，调整邻接矩阵 AG’、行间异或矩阵 RXG’、行间同或矩阵 RAG’对应的行和列；若不匹配，则不同构。 六、结论 基于矩阵变换算法的图同构识别是判断两个无向图是否同构的重要方法，该算法可以通过矩阵变换来实现图同构识别。本资源摘要信息对基于矩阵变换算法的图同构识别进行了详细的知识点总结，为读者提供了一个系统的了解该算法的机会。