### 10-4 磁场对载流导线的作用
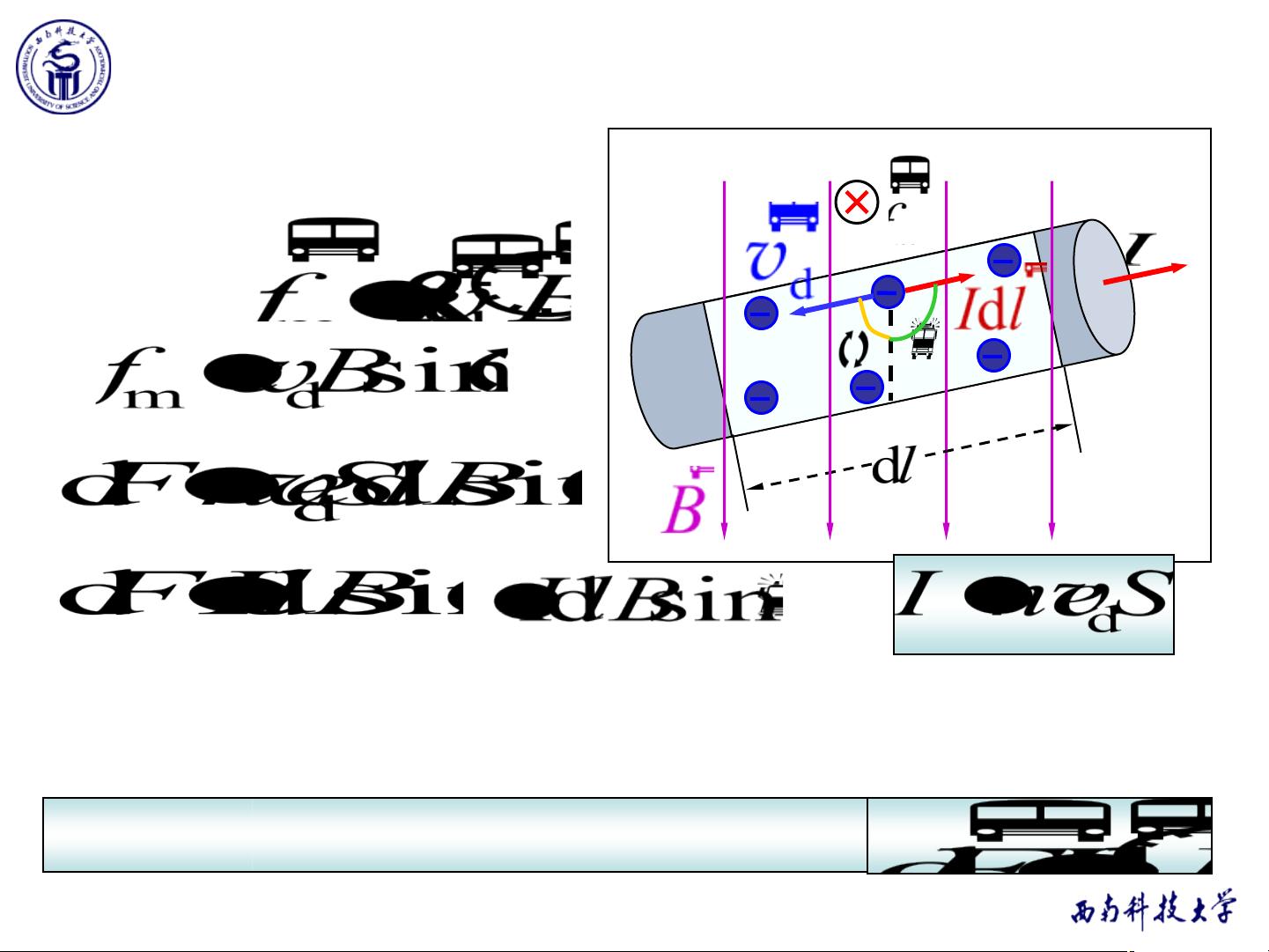
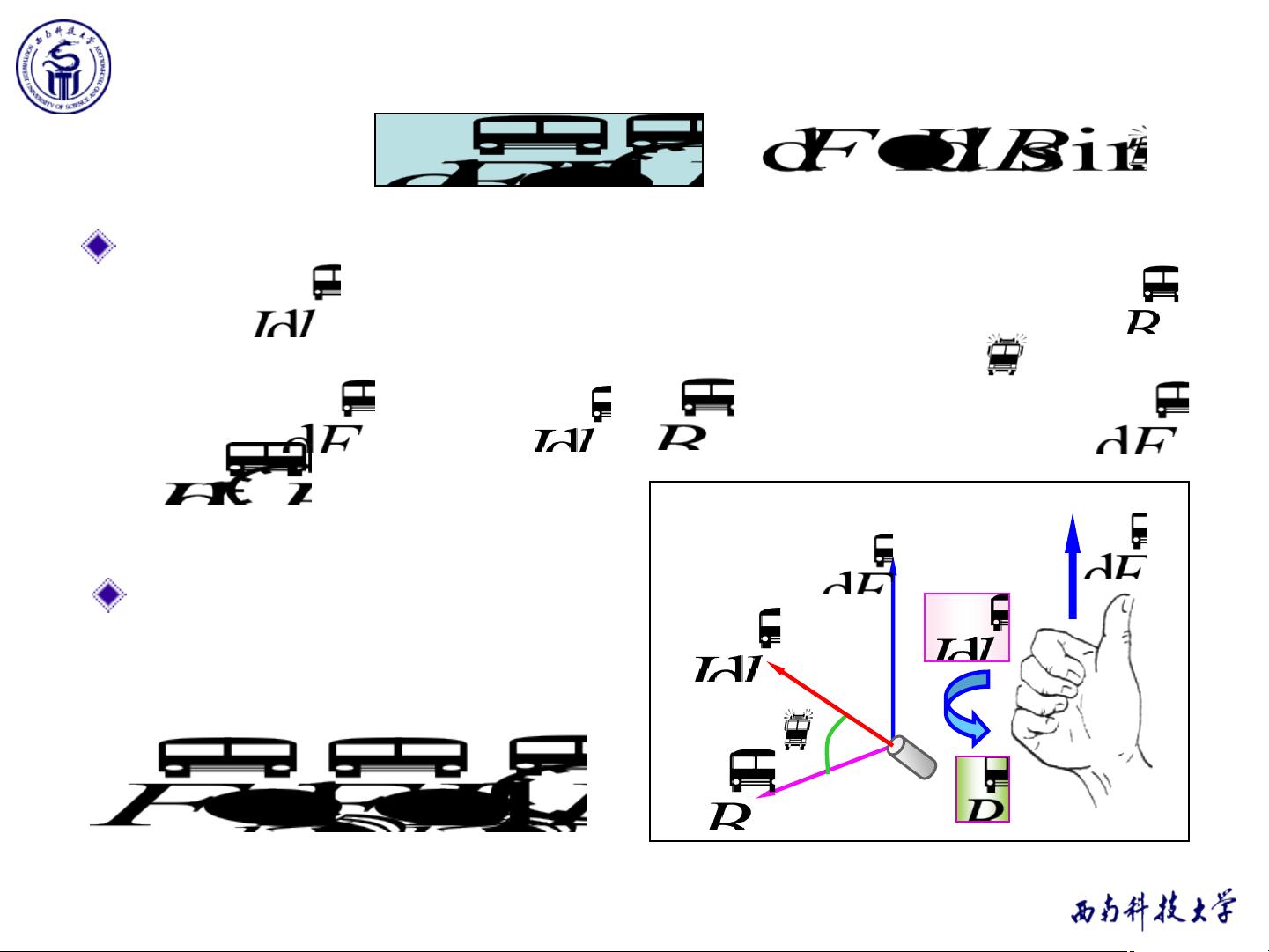
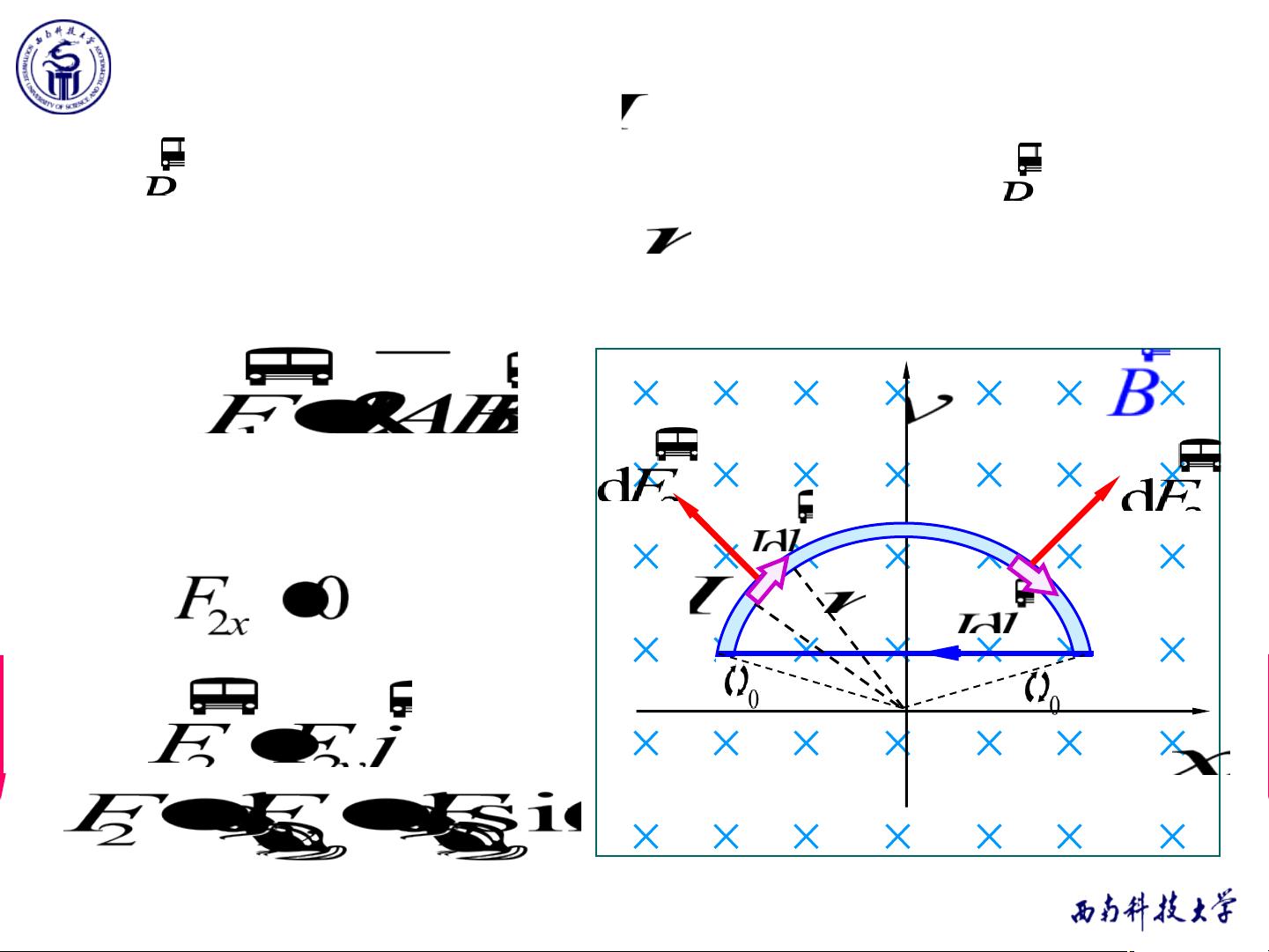
#### 一、安培力与洛伦兹力
磁场对于载流导线的作用力称为安培力，它是电磁学中的一个重要概念。安培力是由洛伦兹力演变而来的一种宏观表现。洛伦兹力是指带电粒子在磁场中运动时所受到的力，其数学表达式为：
\[ \mathbf{F} = q(\mathbf{v} \times \mathbf{B}) \]
其中，\(q\) 是带电量，\(\mathbf{v}\) 是带电粒子的速度矢量，\(\mathbf{B}\) 是磁场矢量。当大量带电粒子在导体中形成电流时，这些粒子的洛伦兹力将转化为导体上的宏观作用力——安培力。
**安培定律** 描述了磁场对载流导线的作用力。对于一个无限小的电流元 \(I d\mathbf{l}\)，它在磁场 \(\mathbf{B}\) 中受到的作用力可以表示为：
\[ d\mathbf{F} = I d\mathbf{l} \times \mathbf{B} \]
这里，\(I\) 表示电流强度，\(d\mathbf{l}\) 是电流元的位移矢量，\(\mathbf{B}\) 是磁场强度。该公式表明作用力的方向垂直于电流元与磁场的方向，并且遵循右手定则。
#### 二、安培力的应用实例
**例1**：考虑一个闭合回路放置在均匀磁场中，回路平面与磁场垂直。假设该回路由一条直线段 AB 和一条半圆形弧线 BCA 组成，电流沿顺时针方向流动。求闭合回路所受的总磁场力。
解析此问题的关键在于理解磁场力是如何分布在整个回路上的。对于直线段 AB 来说，由于磁场方向与电流方向垂直，因此可以利用安培定律计算出直线段所受的磁场力。而对于半圆形弧线 BCA，则需要通过积分的方式来确定其受力情况。最终，通过合成这两部分力的结果，可以得到整个闭合回路所受的总磁场力。
**结论**：对于任意形状的平面载流导线，在均匀磁场中所受的力与导线的起点和终点相同的载流直导线所受的磁场力相同。
**例2**：对于不规则形状的平面载流导线在均匀磁场中的受力问题，同样可以通过分段处理的方法来求解。将导线分成多个小段，然后对每一小段应用安培定律，最后对所有小段的力进行积分即可得到总的磁场力。
**例3**：考虑一个载有电流 \(I\) 的导体圆环与另一条距离圆心为 \(d\) 的长直导线处于同一平面内。求圆环所受的磁场力。该问题可以通过计算圆环上每个点处的磁场力，然后对其进行积分来解决。
#### 三、磁场对载流线圈的作用力矩
磁场不仅会对单个载流导线产生作用力，还会对载流线圈产生力矩。对于一个位于均匀磁场中的矩形载流线圈 MNOP，其力矩可以通过下面的公式计算：
\[ \boldsymbol{\tau} = \mathbf{m} \times \mathbf{B} \]
其中，\(\mathbf{m}\) 表示线圈的磁矩，\(\mathbf{B}\) 表示磁场强度。
**例4**：对于边长为 0.2m 的正方形线圈，共 50 匝，通以电流 2A，放置在磁感应强度为 0.05T 的均匀磁场中。当线圈平面与磁场垂直时，线圈所受的磁力矩最大。此时磁力矩的计算公式为：
\[ \boldsymbol{\tau} = \mathbf{m} \times \mathbf{B} = NIA \times \mathbf{B} \]
其中，\(N\) 是线圈的匝数，\(I\) 是电流强度，\(A\) 是线圈的面积。代入具体数值后可以求得最大磁力矩。
#### 四、电流单位及其定义
国际单位制中电流单位安培(A)的定义是基于两根无限长平行载流直导线间的相互作用力。在真空中，两根相距 1 米的平行长直导线，若它们之间每单位长度上的吸引力为 \(2 \times 10^{-7}\) 牛顿，则导线中通有的电流被定义为 1 安培。
如果两根平行导线中电流方向相反，则它们之间会产生排斥力，而非吸引力。
通过对上述内容的深入探讨，我们可以更好地理解磁场对载流导线的作用原理及其应用，这对于电磁学的学习与实践具有重要意义。
VIP享7折，此内容立减5.97元 
