没有合适的资源?快使用搜索试试~ 我知道了~
2.平面机械的动态静力分析.docx
1.该资源内容由用户上传,如若侵权请联系客服进行举报
2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
版权申诉
0 下载量 143 浏览量
2023-02-27
19:36:54
上传
评论
收藏 691KB DOCX 举报
温馨提示
《平面连杆机构的动态静力分析》章节主要介绍了如何运用解析法,特别是复数矢量法,来进行平面连杆机构的运动分析和设计。在现代技术发展的背景下,解析法和计算机辅助设计成为机械原理课程的重点。教程针对常用机构的分析与设计提供了MATLAB的应用子程序,帮助学生掌握解析法。 章节详细阐述了复数矢量的基本知识。平面矢量可以用复数的形式表示,例如,矢量A可以表示为a + bi,其中a和b分别是矢量在x和y轴上的投影,r是矢量的模,θ是幅角。在MATLAB中,矢量可以表示为如r=3+4*i或r=5*exp(0.34*i)的形式。此外,还介绍了矢量的加减法、乘积和商的运算规则,以及如何在MATLAB中进行这些运算。 接着,章节讨论了刚体和Ⅱ级杆组的运动分析。平面连杆机构可以被看作是基本杆组的组合,通过对基本杆组进行运动分析,可以建立相应的子函数库,进而对整个机构进行运动分析。教程重点讲述了同一构件上两点间的运动分析,包括位置、速度和加速度的计算。通过求解复数矢量方程,可以得到另一点的位置、速度和加速度。 例如,已知一点P的位置、速度和加速度,以及与另一点N的距离r和角度θ,可以利用复数矢量方程来计算N点的运动参数。位置方程为P2 = P + r.e^θi,速度方程为v2 = v + ire^θω,加速度方程为a2 = a - (w^2 - iε)e^(-θi)。这些方程可以转化为MATLAB函数,用于实际计算。 该章节详细介绍了如何使用复数矢量法进行平面连杆机构的动态分析,强调了解析法在机械设计中的重要性,以及MATLAB在解决这类问题时的实用性和效率。通过学习这些知识,学生可以更好地理解和应用解析法解决机械分析和设计问题。
资源推荐
资源详情
资源评论
第 2 章 平面连杆机构的运动分析和动态静力分析
为了适应现代技术的发展,机械原理课程设计方法应由传统的图解法转向以解析法为主,以计算机
为主要设计手段。目前,机械原理教材中对图解法没有详细的论述。为了进行使学生能够熟练地应用解
析法,有必要编制一些常用机构分析与设计的应用子程序。
本指导教程主要有平面连杆机构运动分析、凸轮机构设计标准函数使用方法和实例,供课程设计使
用。所用编程语言为目前流行的数学计算软件-MATLAB,因此,要求学生必须具有 MATLAB 基本运算和
编程基础。考虑到目前有关 MATLAB的参考书较多,本书不再作详细的讲解。
本教程中在平面连杆机构运动分析和动态分析,凸轮机构分析和设计中都应用了复数矢量法,为了
便于学生理解、应用这一方法解决机械分析和设计问题,此处对复数矢量法的一些基本知识和运算方法
作一简单介绍。
2.1 复数矢量的基本知识
解析法对平面机构运动分析和设计的方法很多,目前国内教材中经常应用的有矩阵法、杆组法和矢
量方程法等。根据相关文献的介绍,采用复数矢量方程是解决机构运动学问题的最简单有效的方法,尤
其是平面问题。为了便于理解和应用,这里对复数矢量的一些知识以及复数矢量在 MATLAB 中的运算方
法作一简单介绍。
2.1.1 平面矢量的复数表达式
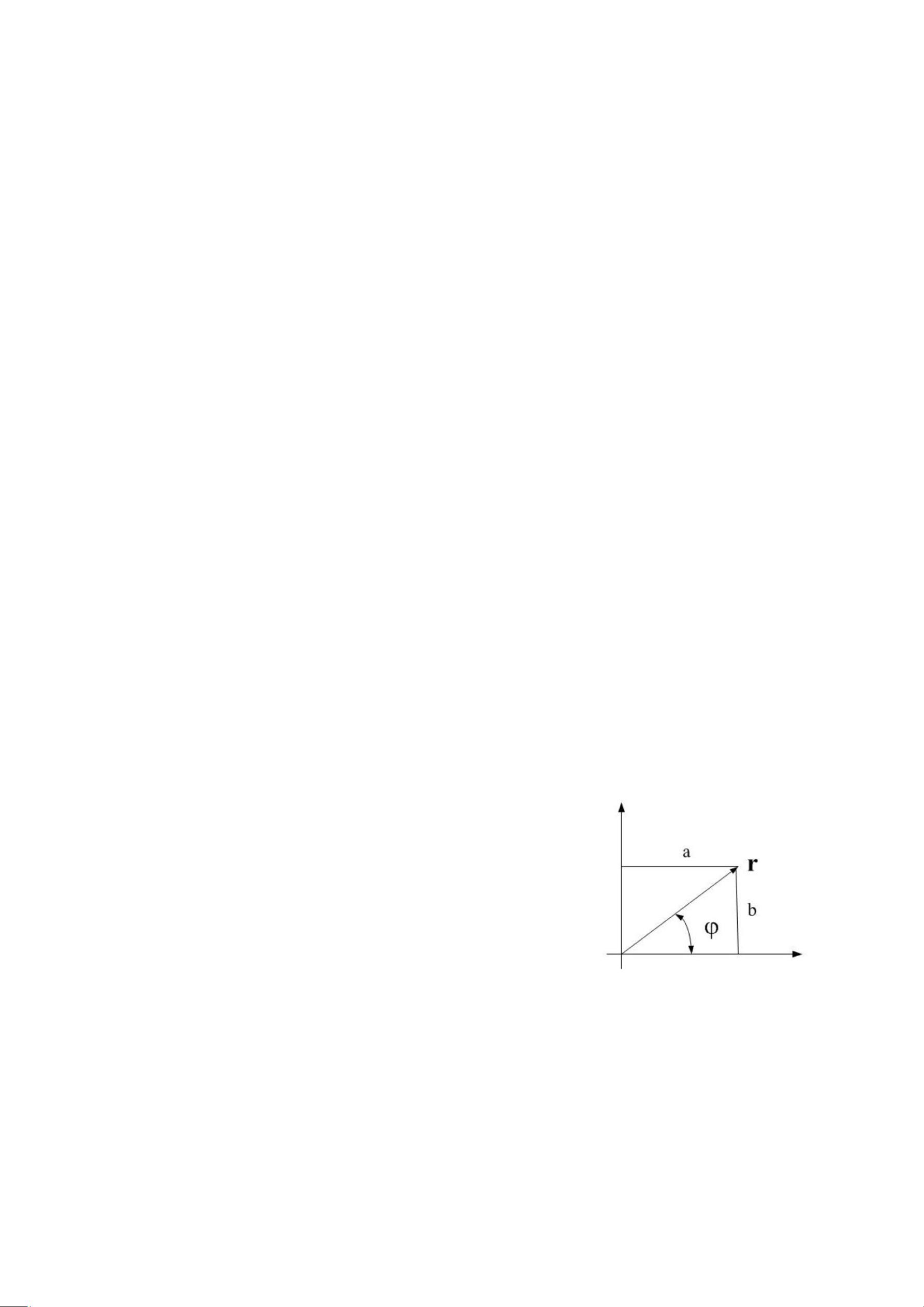
设矢量 A 在坐标轴 x、y 上的投影为 a、b(图 2-1),模为 r,幅角为,以弧度表示。则矢量r 可表
达成复数形式
a bi
r r.e
i
r
或
上式也可以表示 A 点在坐标轴上的位置,在速度和加速度分析中可用来表示某一点的速度、加速度
矢量。
对于一个矢量,若 a=3,b=4,在 MATALAB中其表达式为
r=3+4*i
或 r=5*exp(0.34*i)
2.1.2 矢量的运算
矢量的加(减):两个矢量的加(减)法运算是它们的实部和虚
部分别相加(减)。
a b i
r a b i
若 r
,
1
1
1
2
2
2
r r (a a ) (b b )i
则 r
1
2
1
2
1
2
图 2-1
在 MATLAB中的表达式为:
r1=a1+b1*i; r2=a2+b2i; r=r1+r2;
矢量的乘积和商:两矢量r 和 的乘积是将第一个矢量伸长r 倍,再转动 角度而得到的。
r
1
2
2
2
r.e
r r .e
若 r
,
;
2
i
1
i
1
1
2
2
r r rr .e
则, r
( ) ;
1 2
i
1
2
1 2
r
r r /r
.e
1
( )i
1
2
1
2
r
2
注:作为分母项的矢量不能为零。
r.e r i e
i
复数的微分:
r
i
MATLAB中的相关计算函数:
若 r1=3*exp(4*i),
r2=4*exp(0.2i);
两矢量的乘除: rm=r1.*r2;rd=r1./r2;注:两矢量的点乘、点除为两矢量对应项的乘、除。
如果已知矢量 a,则可以通过下列运算求出复数的相关量,
复数的模:
abs(a); 复数的幅角:
angle(a);
复数 a 的实部: real(a): 复数的虚部:
复数 a 的共轭复数: conj(rd);
imag(a);
2.2 刚体和Ⅱ级杆组的运动分析
由机构组成原理可知,任何平面连杆机构都可以看作是由若干个基本杆组依次连接于原动件和机架
上而构成。因此对常见的基本杆组进行运动分析并建立相应的子函数库,在进行机构运动分析时,就可
以根据机构的组成情况,将机构分解为原动件、机构和若干个基本杆组,编制一个调用该机构杆组子函
数的主程序,即可实现对整个机构的运动分析。
考虑到工程实际中大多数机构是Ⅱ级机构,本节主要介绍同一构件上两点间的运动分析和最常见的
RRR 型、RRP 型和 RPR 型Ⅱ级杆组的运动分析的子函数,并通过一个典型的实例说明用该方法进行机构
运动分析的方法和步骤。
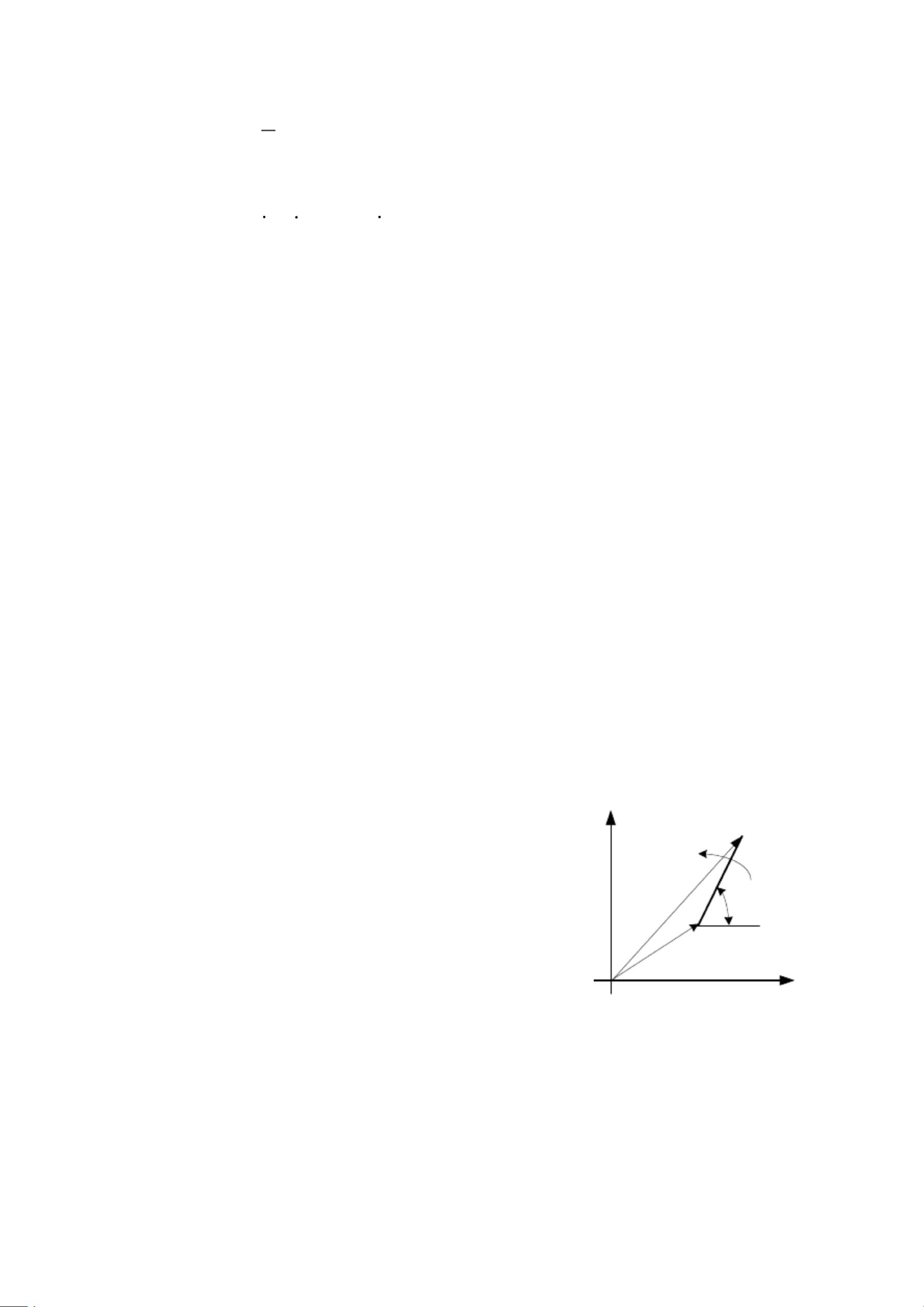
2.2.1 同一构件上的点的运动分析
已知构件上一点的位置矢量 P, 速度 v 、加速度 a , P P 两点间距离 r 和位置角(以 x 轴为起始线
1
1
1
1 2
逆时针方向为正),角速度、角加速度 。求构件上另一点 N 点的位置、速度和加速度。
2
由图可得位置的复数矢量方程为
y
P
2
P P r.e
i
(2-1)
2
1
,
a
式(2-1)对时间 t 求导,即得 N 点速度的复数矢量方程
2
r
v v ire
i
(2-2)
P
2
1
1
1
同样,式(2-2)对时间 t 求导可得 P 点的加速度复数矢量方程
2
x
图 2-2
a a ir e
r e
i
2
i
(2-3)
1
2
根据以上矢量方程编制的求 P 点位置、速度、加速度的函数为:
2
function [a2,v2,p2]=rigid(a1,v1,p1,w,e1,r,theta)
p2=p1+r*exp(i*theta);
v2=v1+i*r*w.*exp(i*theta);
a2=a1-(w.^2-i*e1).*r.*exp(i*theta);
其中:p,v,a 是以复数形式给出的相应点的位置、速度和加速度矢量。
-theta,角度;w- 角速度;e1-,角加速度
当 P 为固定铰链点时,求解时只需使 v =0,a =0 即可。这样就可用来求主动件曲柄上某一点的运动
1
1
1
参数。
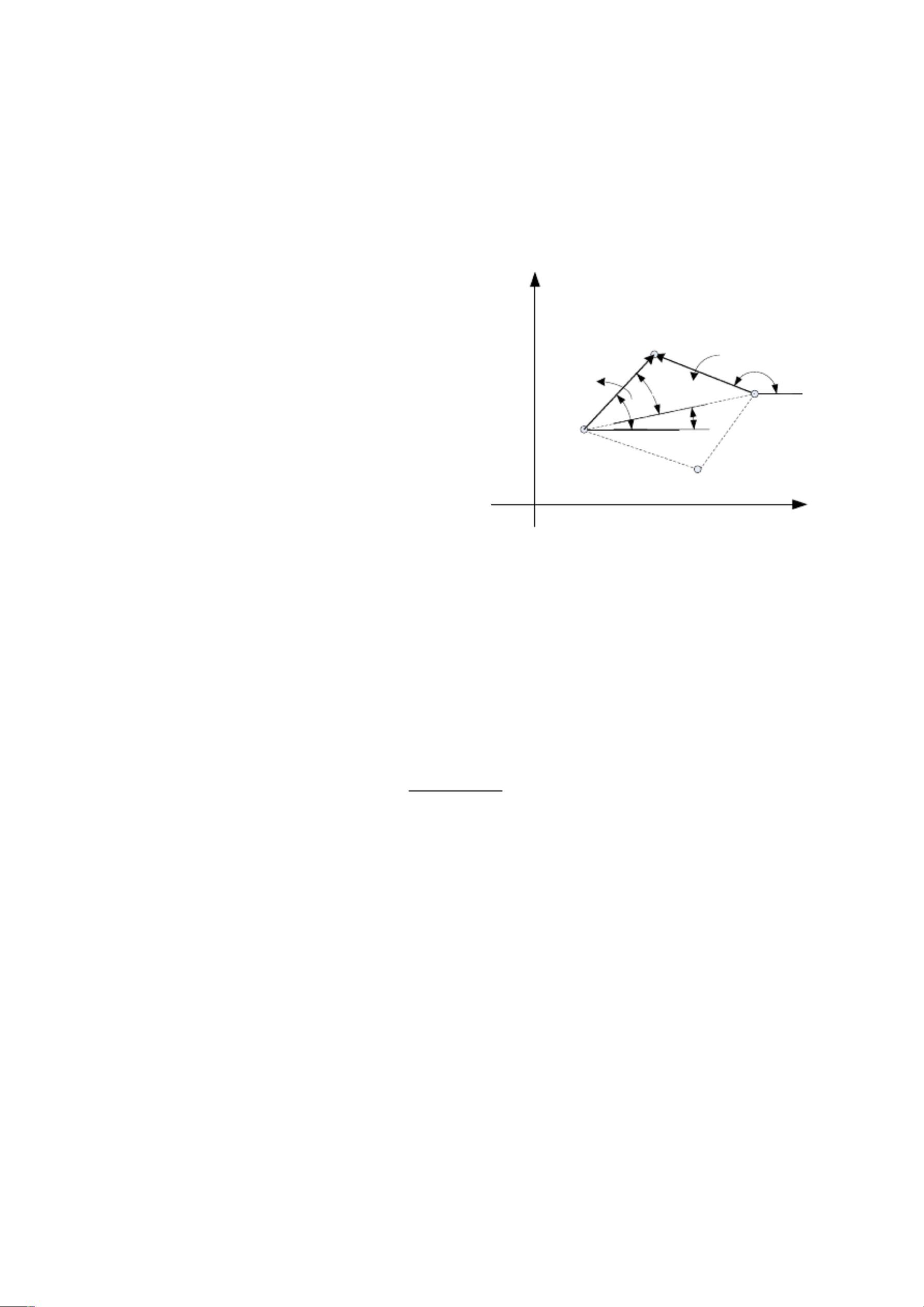
2.2.2 RRR基本杆组运动分析
y
RRRⅡ级基本杆组由两个构件和三个转动副构成,
如图 2-3 所示。已知:两构件杆长分别为 r 和 r 、,两
2
l
2
2
r
2
外接运动副 P 、P 的运动矢量参数(p ,v ,a 和 p 、v 、
1
r
1
1
2
1
1
2
2
a
a )。求内接转动副 P 点位置、速度、加速度及两构件
3
d
,
1
1
2
的角速度、角加速度。
1. 位置分析
P '
2
P P 间的矢量d 为
1
2
x
d P P
(2-4)
2
1
图 2-3
求出矢量 d 的模 d 和幅角
d=abs(d),
=angle(d)
(2-5)
r r d | r r |
根据它们之间的几何关系,若d
或
,则 RRR 杆组不能装配。在程序运行中应进
1
2
1
2
行判断。
P P
与 d 之间的夹角为
1
2
r d r
2
2
2
cos
1
a
(2-6)
(2-7)
1
2
2r d
1
a
而
1
式(2-7) 前的正负号决定于杆组起始位置的安装形式。如图
a
2-3
中实线方式装配(构成
P P P
顺
1
3
2
P P 'P
时针方向)时,取正号;若按图中虚线方式装配(构成
逆时针方向)时,则取负号.
1
3
2
节点P 的位置为
3
p = p +r e
(2-8)
(2-9)
i
1
3
1
1
angle(p -p )
2
3
2
2. 速度分析
P
式(2-8)对时间求导得 的速度矢量方程为
3

v - v =r ie
i
1
3
1
1 1
v - v r ie
(2-10)
(2-11)
i
2
3
2
2 2
上两式相减得:
v - v r ie -r ie
i
i
2
1
2
1
1
1
2
2
abs(v - v )
angle(v - v )
令: v
,
21m
2
1
v
2
1
则式(2-11)可写成:
v e
r ie
-r ie
(2-12)
(2-13)
i
i
i
2
1
v
12m
1
1
2
2
求解得
v cos( )
21m
r
1
2
v
sin( )
1
1
2
v cos( )
(2-14)
(2-15)
21m
1
v
r
sin( )
2
2
2
1
v v r ie
i
1
则:
1 1
3
1
3.加速度分析
式(2-10)对时间 t 求导后,可得点P 的加速度复数矢量方程:
3
a -a r ie r e
2
i
1
i
1
(2-16)
3
1
1
1
1
1
a -a r ie r e
i
2
i
2
2
3
2
2
2
2
2
上两式相减得
a -a r ie r e r ie r e
i
2
i
2
1
i
i
2
2
(2-17)
1
1
2
1
1
1
1
2
2
2
2
abs(a -a )
,
angle(a -a )
令: a
21m
2
1
a
2
1
则上式可表示为
a e r ie r e r ie r e
2
1
2
2 i
1
i
2
2 i
(2-18)
i
i
1
1
a
21m
1
1
2
2
2
由此解得
r
a cos( ) r cos( )
2
1
2
2
1
(2-19)
(2-20)
21m
2
a
1
2
1
2
2
r
sin( )
1
1
2
r
a cos( ) r cos( )
2
2
21m
1
a
2
1
2
1 1
r
sin( )
2
2
2
1
剩余24页未读,继续阅读
资源评论

xxpr_ybgg
- 粉丝: 6759
- 资源: 3万+
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功