Matlab笔记-模糊聚类分析原理及实现.pdf
2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
模糊聚类分析是一种在数据分析中用于分类的方法,它源于模糊理论,相较于传统的硬划分聚类,模糊聚类更能反映现实世界的不确定性。在模糊聚类中,样本不再被严格分配到某一个类别,而是可能属于多个类别,且程度不同。这使得分类边界变得模糊,能够更好地处理数据的复杂性和不确定性。 在模糊聚类中,有两个重要的概念:模糊等价矩阵和模糊矩阵的λ-截矩阵。模糊等价矩阵是描述对象间模糊相似关系的矩阵,满足自反性、对称性和传递性。自反性意味着每个对象与自身的关系是确定的,对称性表示如果对象A与B相似,那么B也与A相似,传递性则指如果A与B相似,B与C相似,那么A与C也相似。模糊等价矩阵可以通过传递闭包矩阵Rk找到最小的k,使得Rk成为模糊等价矩阵。 模糊矩阵的λ-截矩阵则是将模糊矩阵转换为布尔矩阵的工具,通过设定阈值λ,将大于λ的元素置为1,小于λ的置为0。当λ变化时,可以得到不同的分类结果,形成一个分级聚类树。例如,当λ增大,分类会变得更细,更强调对象之间的差异;反之,当λ减小,分类会合并,体现对象间的相似性。 基于择近原则的模糊聚类是通过计算模糊集A和B的贴近度N(A,B)来实现分类的。常见的贴近度计算方法有海明贴近度、欧氏贴近度和格贴近度。海明贴近度考虑的是两个模糊集在每个元素上的差异,欧氏贴近度基于平方和的平方根,而格贴近度则结合了集合的交集和补集,体现了集合的覆盖程度。 在MATLAB中,可以编写函数如`fuz_closing.m`来实现模糊聚类中的格贴近度计算。这个函数接受两个向量A和B,以及类型参数type,根据type的值计算海明贴近度或格贴近度。这样的函数可以作为构建模糊聚类算法的基础。 模糊聚类分析是一种灵活且适应性强的分类方法,特别适用于处理具有不确定性和复杂性的数据。通过模糊等价矩阵和λ-截矩阵的概念,我们可以更好地理解和实现模糊聚类。在实际应用中,如互联网数据分析、计算机科学等领域,模糊聚类能够提供更为真实和细致的分类结果,帮助我们揭示隐藏在数据背后的模式和规律。

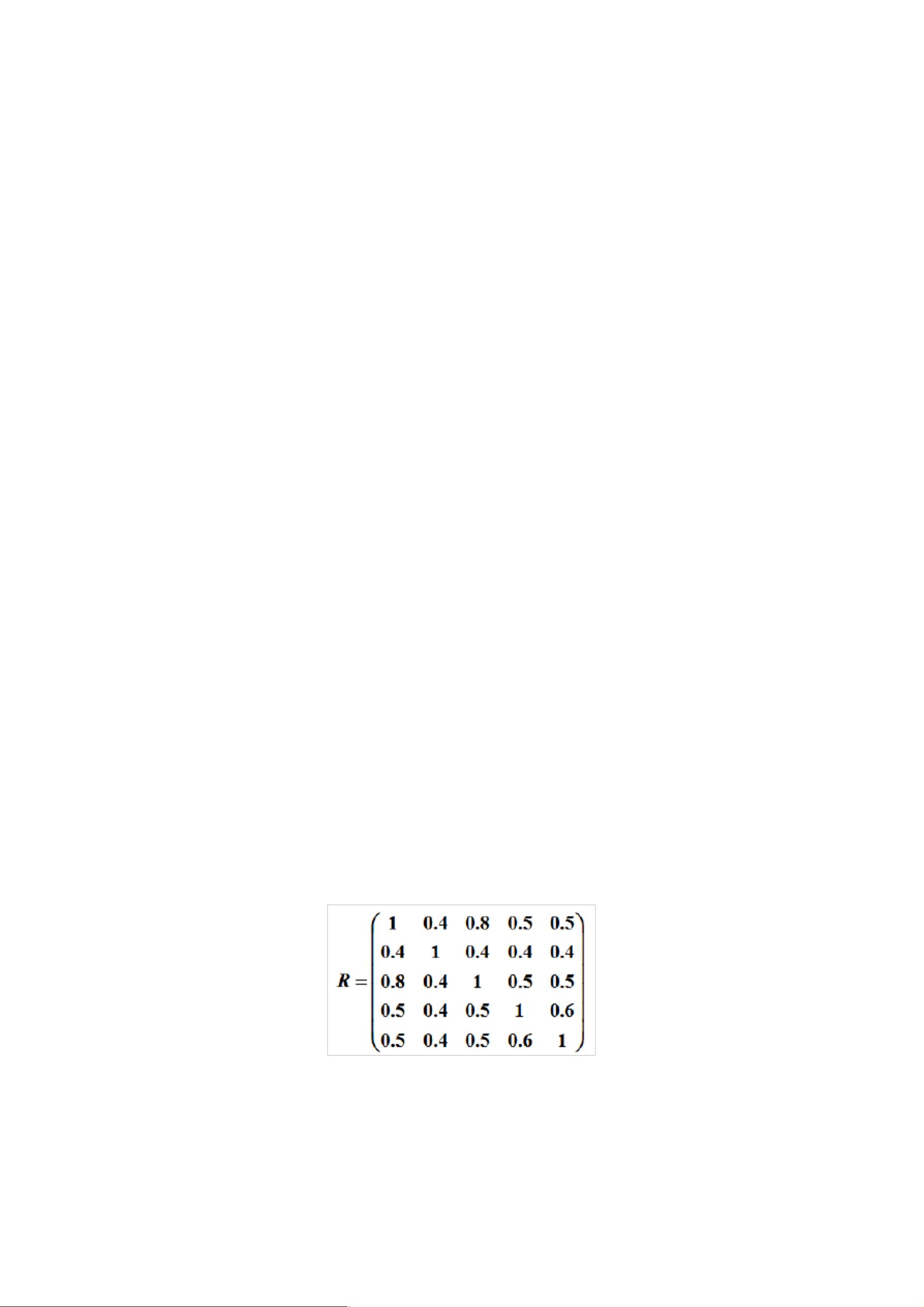

剩余14页未读,继续阅读

- 粉丝: 6788
- 资源: 3万+
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功