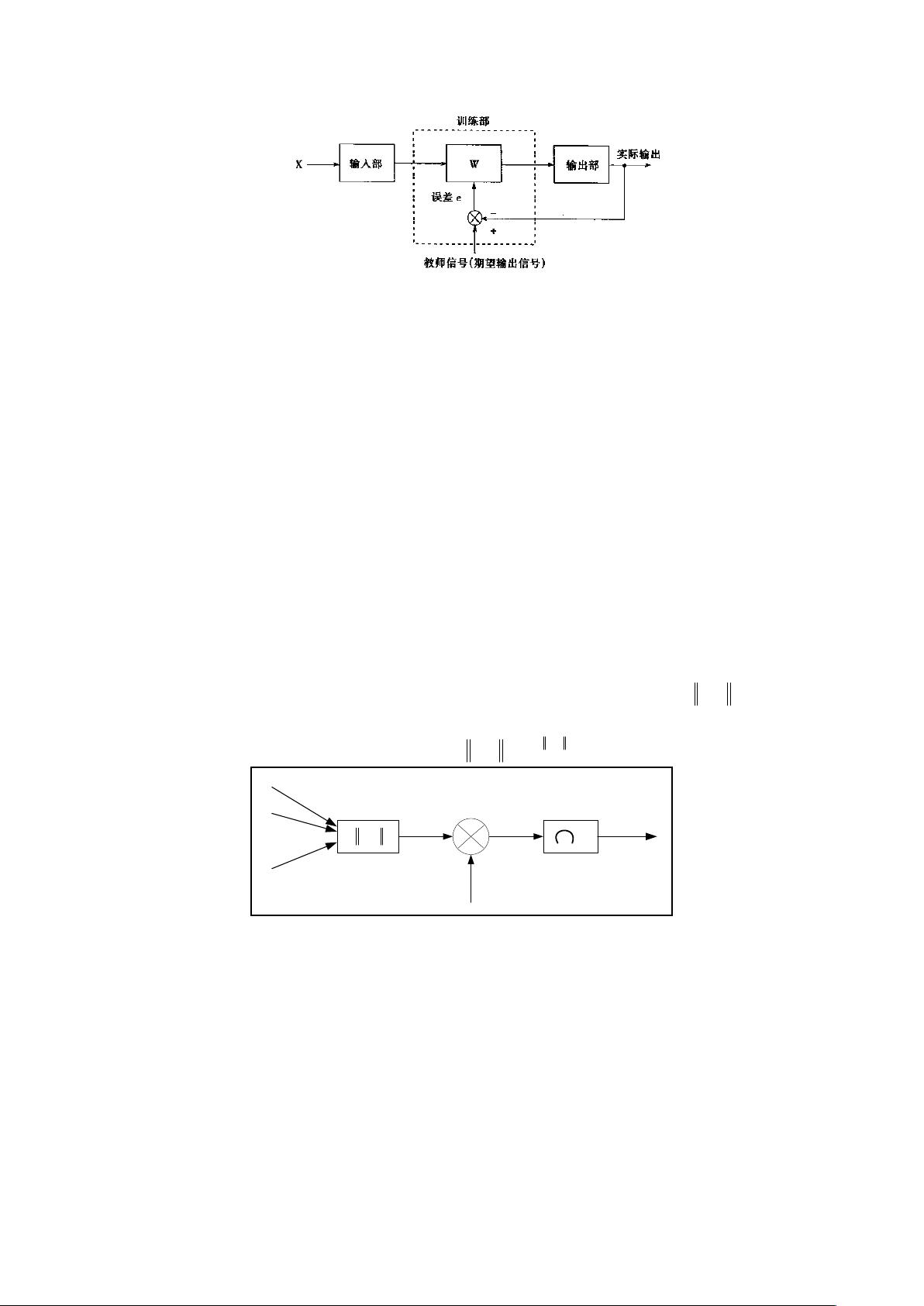
图 2 神经网络的训练
2.2 RBF神经网络
2.2.1 RBF 神经网络概述
1985 年,Powell 提出了多变量插值的径向基函数(Radical Basis Function, RBF)方
法。1988 年,Moody 和 Darken 提出了一种神经网络结构,即 RBF 神经网络,属于前向神经
网络类型,它能够以任意精度逼近任意连续函数,特别适合于解决分类问题。
RBF 网络的结构与多层前向网络类似,它是一种三层前向网络。输入层由信号源节点组
成;第二层为隐含层,隐单元数视所描述问题的需要而定,隐单元的变换函数 RBF()是对
中心点径向对称且衰减的非负非线性函数;第三层为输出层,它对输入模式的作用作出响应。
从输入空间到隐含层空间的变换是非线性的,而从隐含层空间的输出层空间变换是线性的。
RBF 网络的基本思想是:用 RBF 作为隐单元的“基”构成隐含层空间,这样就可以将输
入向量直接(即不需要通过权接)映射到隐空间。当 RBF 的中心点确定以后,这种映射关系
也就确定了。而隐含层空间到输出空间的映射是线性的,即网络的输出是隐单元输出的线性
加权和。此处的权即为网络可调参数。由此可见,从总体上看,网络由输入到输出的映射是
非线性的,而网络输出对可调参数而言却又是线性的。这样网络的权就可由线性方程直接解
出,从而大大加快学习速度并避免局部极小问题。
径向基神经网络的神经元结构如图 3 所示。径向基神经网络的激活函数采用径向基函数,
通常定义为空间任一点到某一中心之间欧氏距离的单调函数。由图 3 所示的径向基神经元结
构可以看出,径向基神经网络的激活函数是以输入向量和权值向量之间的距离 作为自
变量的。径向基神经网络的激活函数(高斯函数)的一般表达式为
图 3 径向基神经元模型
随着权值和输入向量之间距离的减少,网络输出是递增的,当输入向量和权值向量一致
时,神经元输出 1。在图 3 中的 b 为阈值,用于调整神经元的灵敏度。利用径向基神经元和
线性神经元可以建立广义回归神经网络,该种神经网络适用于函数逼近方面的应用;径向基
神经元和竞争神经元可以组建概率神经网络,此种神经网络适用于解决分类问题。
由输入层、隐含层和输出层构成的一般径向基神经网络结构如图 4 所示。
评论0
最新资源