算法用回溯法(backtracking algorithm)求解N皇后问题(N-Queens puzzle).docx

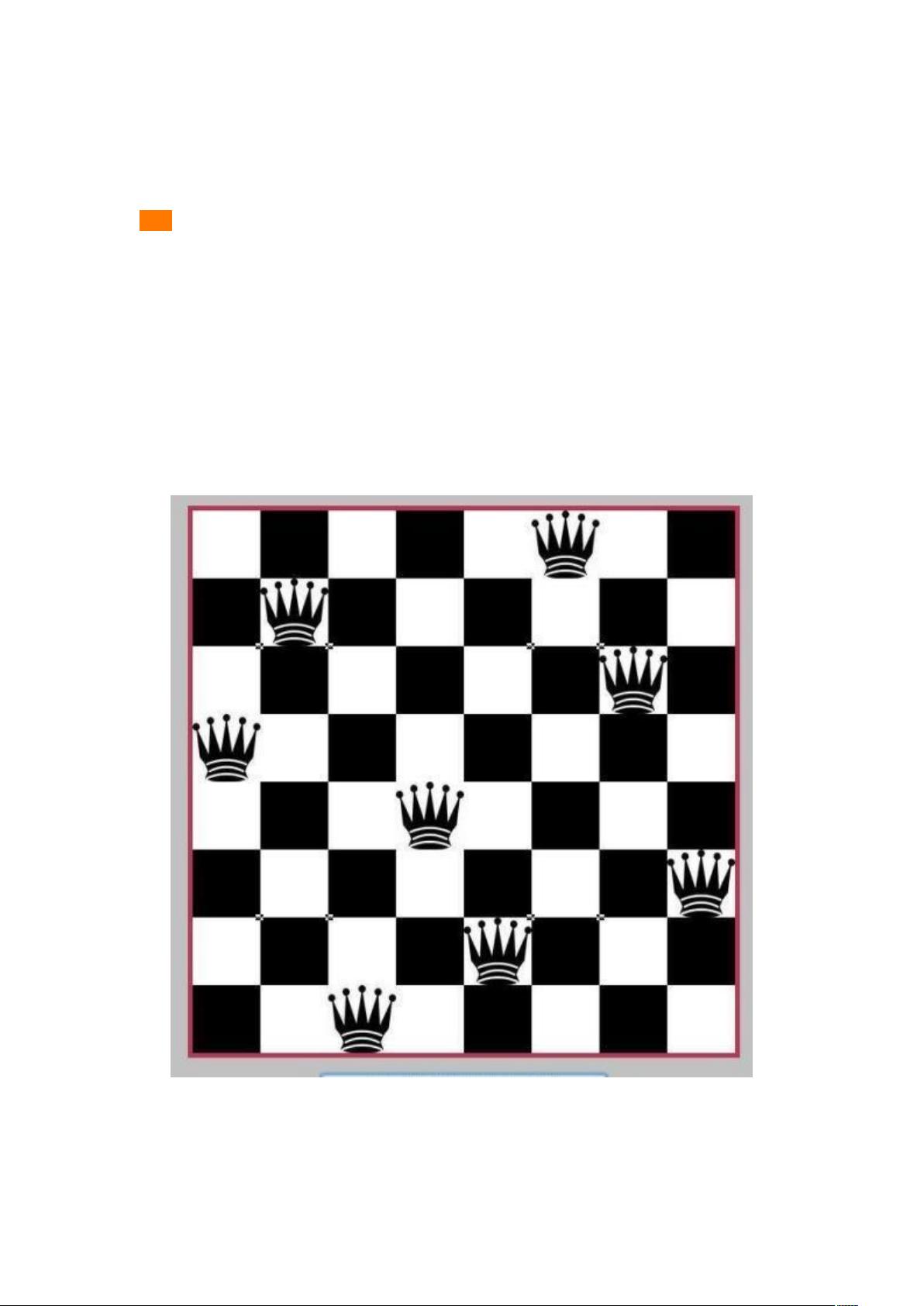
回溯算法解决 N 皇后问题 N 皇后问题是一个经典的问题，在一个 NxN 的棋盘上放置 N 个皇后，使其不能互相攻击（同一行、同一列、同一斜线上的皇后都会自动攻击），那么问，有多少种摆法？回溯算法（backtracking algorithm）是解决 N 皇后问题的一种有效方法。下面是对回溯算法的详细说明： 定义：回溯算法实际上是一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。 基本思想：回溯算法的基本思想是，从一条路往前走，能进则进，不能进则退回来，换一条路再试。在包含问题的所有解的解空间树中，按照深度优先搜索的策略，从根结点出发深度探索解空间树。当探索到某一结点时，要先判断该结点是否包含问题的解，如果包含，就从该结点出发继续探索下去，如果该结点不包含问题的解，则逐层向其祖先结点回溯。 解决问题的一般步骤： 1. 针对所给问题，定义问题的解空间，它至少包含问题的一个（最优）解。 2. 确定易于搜索的解空间结构，使得能用回溯法方便地搜索整个解空间。 3. 以深度优先的方式搜索解空间，并且在搜索过程中用剪枝函数避免无效搜索。 回溯法的工作方式： 1. 确定了解空间的组织结构后，回溯法就从开始结点（根结点）出发，以深度优先的方式搜索整个解空间。 2. 这个开始结点就成为一个活结点，同时也成为当前的扩展结点。 3. 在当前的扩展结点处，搜索向纵深方向移至一个新结点。 4. 这个新结点就成为一个新的活结点，并成为当前扩展结点。 5. 如果在当前的扩展结点处不能再向纵深方向移动，则当前扩展结点就成为死结点。 6. 此时，应往回移动（回溯）至最近的一个活结点处，并使这个活结点成为当前的扩展结点。 解空间和解空间树： 1. 解空间是一个复杂问题的解决方案，由多部分构成。 2. 解空间中满足约束条件的决策序列称为可行解。 3. 一般说来，解任何问题都有一个目标，在约束条件下使目标值达到最大（或最小）的可行解称为该问题的最优解。 4. 在解空间中，前 k 项决策已经取定的所有决策序列之集，称为 k 定子解空间。0 定子解空间即是该问题的解空间。 算法框架： void backtrack (int t){ if (t>n) { output(x); //叶子节点，输出结果，x 是可行解 } else { for i = 1 to k//当前节点的所有子节点 { x[t]=value(i); //每个子节点的值赋值给 x //满足约束条件和限界条件 if (constraint(t)&&bound(t)) backtrack(t+1); //递归下一层 } } } 这篇文章详细介绍了回溯算法和 N 皇后问题，并提供了回溯算法的定义、基本思想、解决问题的一般步骤、回溯法的工作方式、解空间和解空间树、算法框架等内容，为读者提供了一个系统的了解回溯算法和 N 皇后问题的机会。