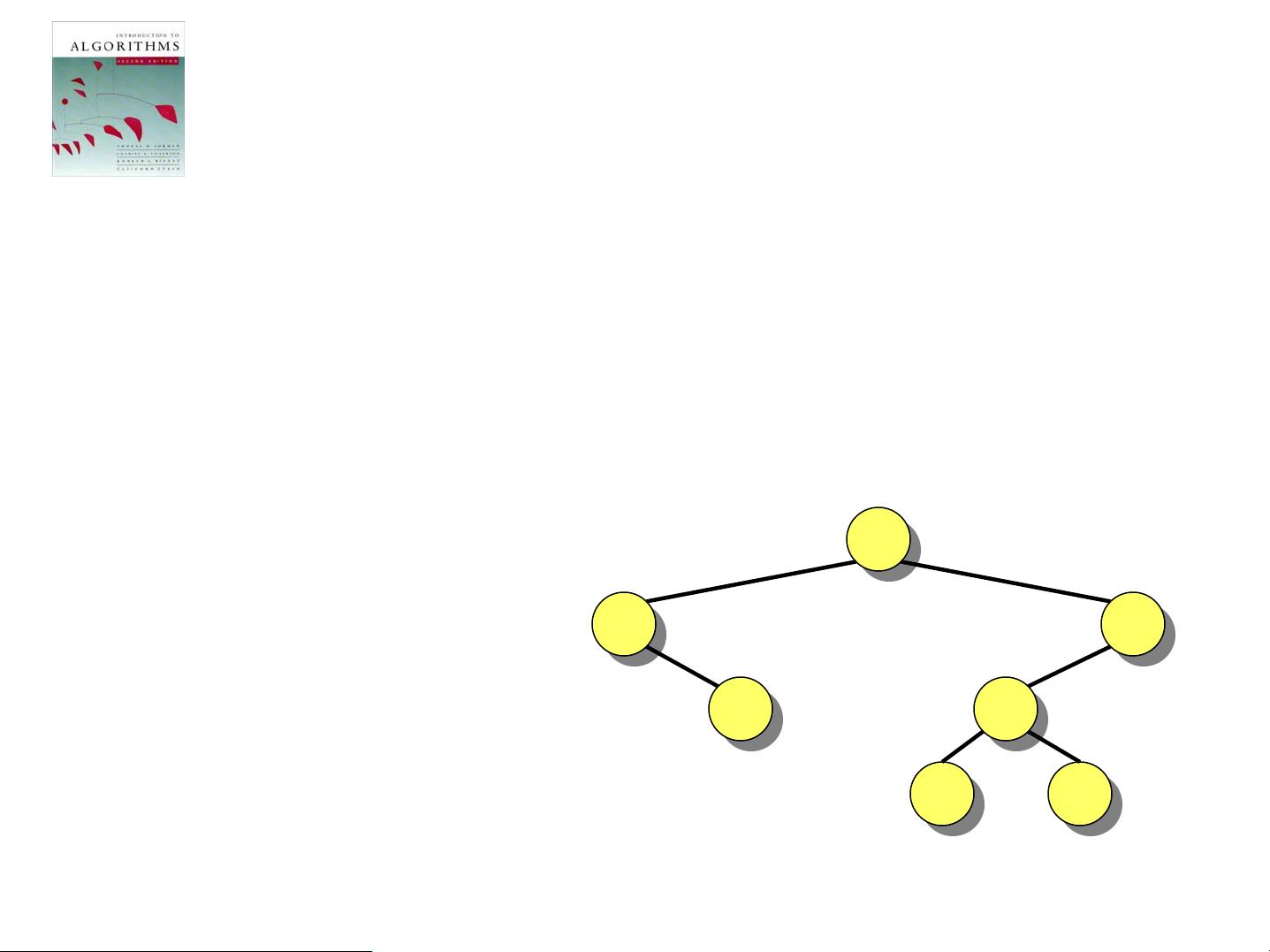
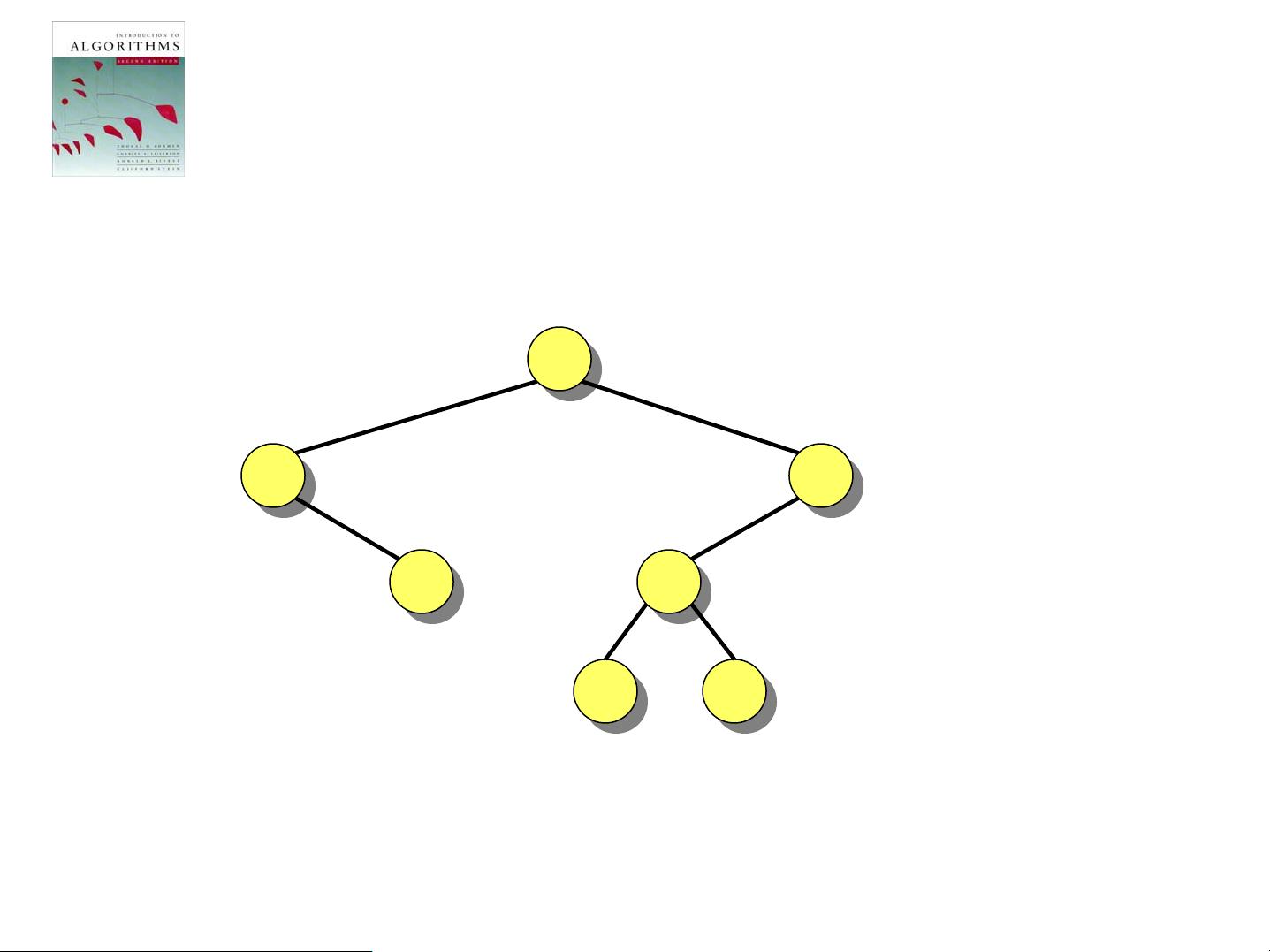
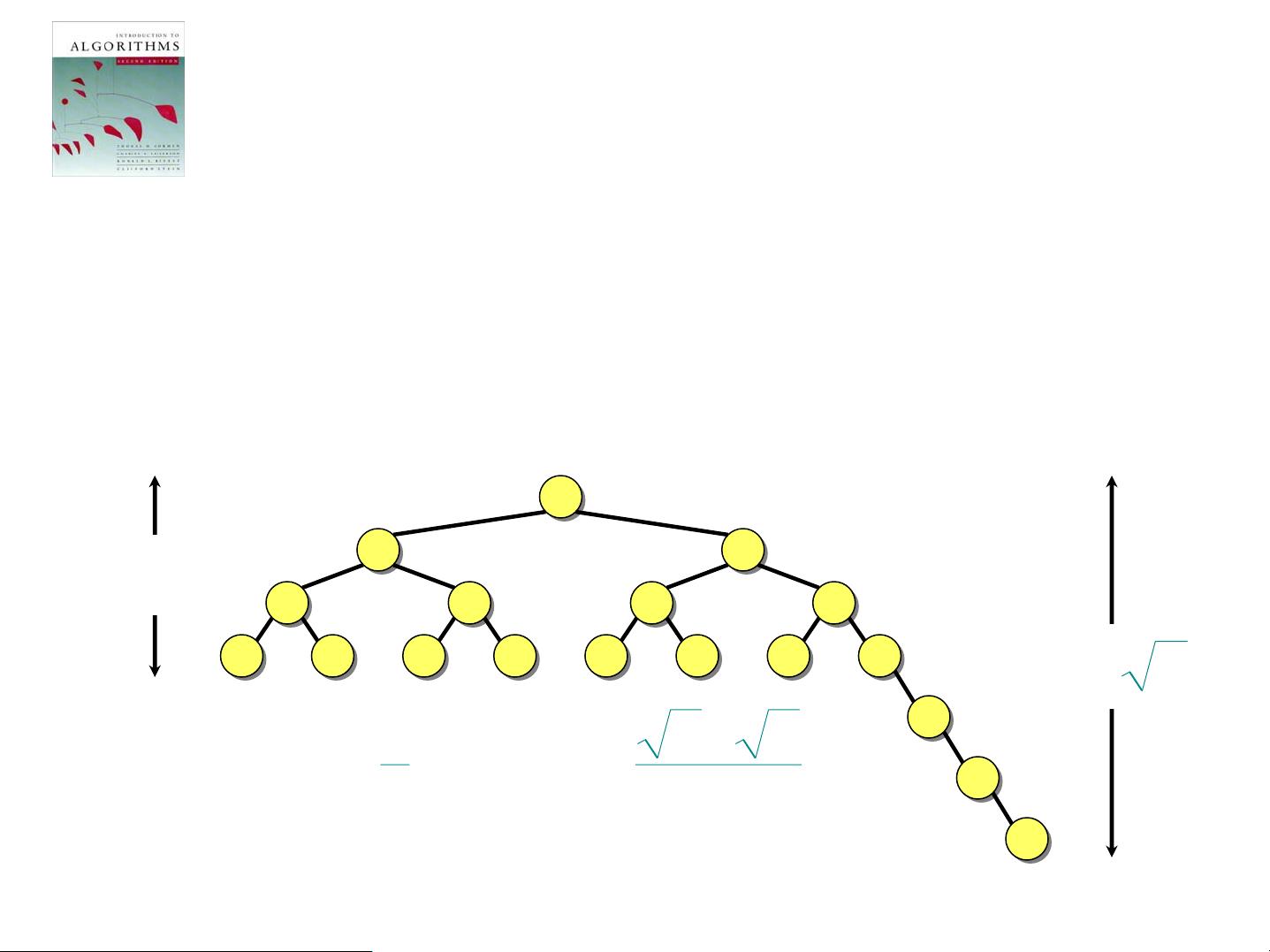
《算法导论》原版英文课件9

### 《算法导论》原版英文课件9：二叉搜索树与快速排序的关系 #### 关键知识点 1. **二叉搜索树(Binary Search Tree, BST)与快速排序(Quicksort)的关系** - **关系概述**：在本节课件中，作者通过分析随机构建的二叉搜索树来探讨其与快速排序之间的联系。 - **相同性**：快速排序和二叉搜索树排序执行相同的比较操作，但顺序不同。 - **时间复杂度**：构建二叉搜索树的时间复杂度与快速排序的时间复杂度是渐近相同的。 2. **节点深度分析** - **定义**：节点深度指的是在二叉搜索树中插入一个节点时进行的比较次数。 - **平均节点深度**：如果所有输入排列都等概率出现，则平均节点深度为\(O(\log n)\)。 - **公式**： \[ E(\text{depth of node}) = \sum_{i=1}^{n} \frac{\log (n+1-i)}{n} = O(\log n) \] 3. **随机构建的二叉搜索树的高度分析** - **概念**：即使随机构建的二叉搜索树的平均节点深度为\(O(\log n)\)，其高度也可能不是\(O(\log n)\)。 - **示例**：给出一个例子，展示即使平均节点深度较小，树的高度仍可能较大。 - **公式**：给出一个具体的公式来计算树的平均高度。 \[ \text{Average depth} \leq \log n \Rightarrow \sum_{n=1}^{n} \frac{n \cdot \log (n+1-i)}{n} \leq O(n \cdot \log n) \] 4. **凸函数与詹森不等式(Jensen's Inequality)** - **定义**：函数\(f : \mathbb{R} \rightarrow \mathbb{R}\)被称为凸函数，如果对于所有\(x\)和\(y\)以及\(0 \leq \theta \leq 1\)，有 \[ f(\theta x + (1-\theta)y) \leq \theta f(x) + (1-\theta)f(y) \] - **詹森不等式**：对于任意凸函数\(f\)和随机变量\(X\)，有 \[ f(E[X]) \leq E[f(X)] \] - **应用**：利用詹森不等式证明随机构建的二叉搜索树的期望高度为\(O(\log n)\)。 5. **指数高度分析** - **定义**：指数高度\(Y_n = 2^{X_n}\)，其中\(X_n\)是随机变量，表示随机构建的二叉搜索树的高度。 - **证明**：证明\(2^{E[X_n]} \leq E[2^{X_n}] = E[Y_n] = O(n^3)\)，从而得出\(E[X_n] = O(\log n)\)。 6. **后记(Postmortem)** - **总结**：对整节课件中的关键点进行总结，强调通过这些分析方法可以更好地理解随机构建的二叉搜索树的行为及其与快速排序的关系。 - **教授**：由Erik Demaine教授主讲。 #### 结论 本节课件深入探讨了随机构建的二叉搜索树的各种属性，并将其与快速排序进行了对比。通过对节点深度、树的高度、凸函数及詹森不等式的讨论，读者可以更深刻地理解这些数据结构和算法的核心概念。此外，通过对随机变量和凸函数的应用，我们能够推导出随机构建的二叉搜索树的期望高度为\(O(\log n)\)，这表明在随机情况下，这种类型的二叉搜索树具有良好的性能。