梯形辅助线作法总结整理.pdf

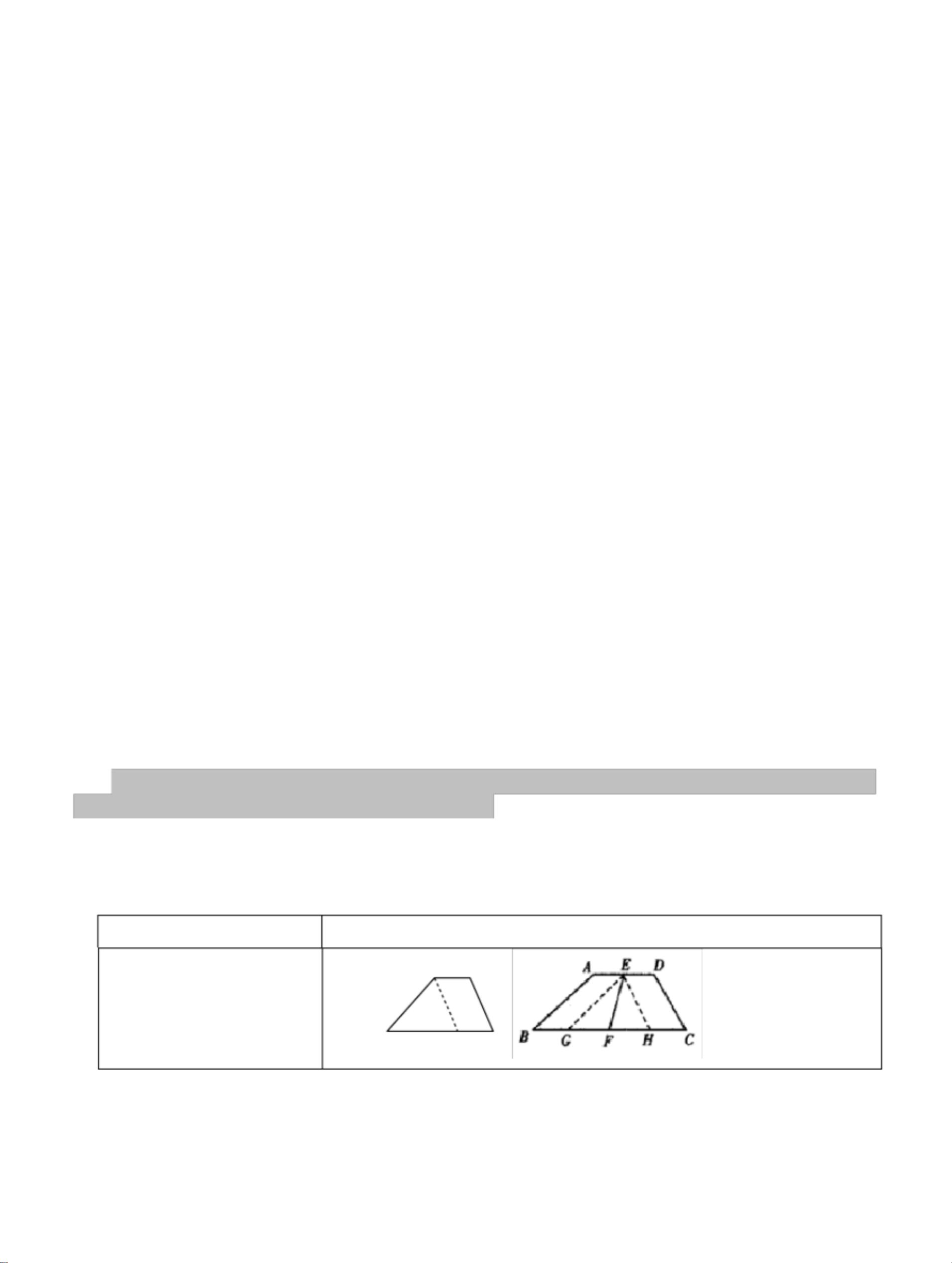
在梯形问题的解决中，添加辅助线是关键策略，能够将复杂的梯形问题转化为更为简单和熟悉的平行四边形或三角形问题。以下是一些常见的梯形辅助线作法及其应用实例： 1. **平移一腰**： - 例如在直角梯形ABCD中，可以过点D作DE∥BC，这样四边形BCDE成为平行四边形，利用平行四边形的性质可以求解梯形的未知边长。如例1所示，通过此方法可以找到CD的长度。 2. **平移两腰**： - 在某些情况下，可能需要同时平移两个非平行边，将梯形转化为三角形或平行四边形，以便利用三角形的性质进行计算。如例2所示，过点B作BM∥AD，可以确定另一腰BC的取值范围。 3. **延长两腰**： - 将两个非平行边延长，使其在某点相交，可以将梯形转化为三角形。如例7，延长BA和CD至点E，然后在三角形BEC中解决问题，这在求解角度和边长时特别有用。 4. **平移对角线**： - 如例4，作DE∥AC，可以将梯形转化为包含一个直角的特殊形状，从而计算出梯形的面积。 5. **作高**： - 当梯形包含直角时，作高可以将梯形转化为直角三角形和矩形，便于利用勾股定理和矩形的性质。如例3，通过构造直角三角形EGH，可以求解EF的长度。 6. **连接腰的中点**： - 如果已知腰的中点，可以连接它们或者过一腰中点作另一腰的平行线。如例6，过D作DE∥AC，利用平行四边形ACED的性质求解梯形面积。 7. **作中位线**： - 若题目涉及梯形的中位线，可以直接连接相对顶点的中点，形成中位线，然后利用中位线的性质解决问题。 8. **过一腰的中点作平行线**： - 如例5，过C作CE∥BD，使得四边形BCED为平行四边形，进一步证明AC垂直于BD。 以上这些辅助线的添加方法并不是孤立的，根据具体题目条件，可能需要灵活组合运用。在选择辅助线时，应根据图形特征、已知条件以及需要解决的问题来确定最佳方案。辅助线的巧妙运用是解决梯形问题的关键，能够帮助我们有效地将复杂问题简化为基本几何图形的性质。