关于算法复杂度的概念的PPT

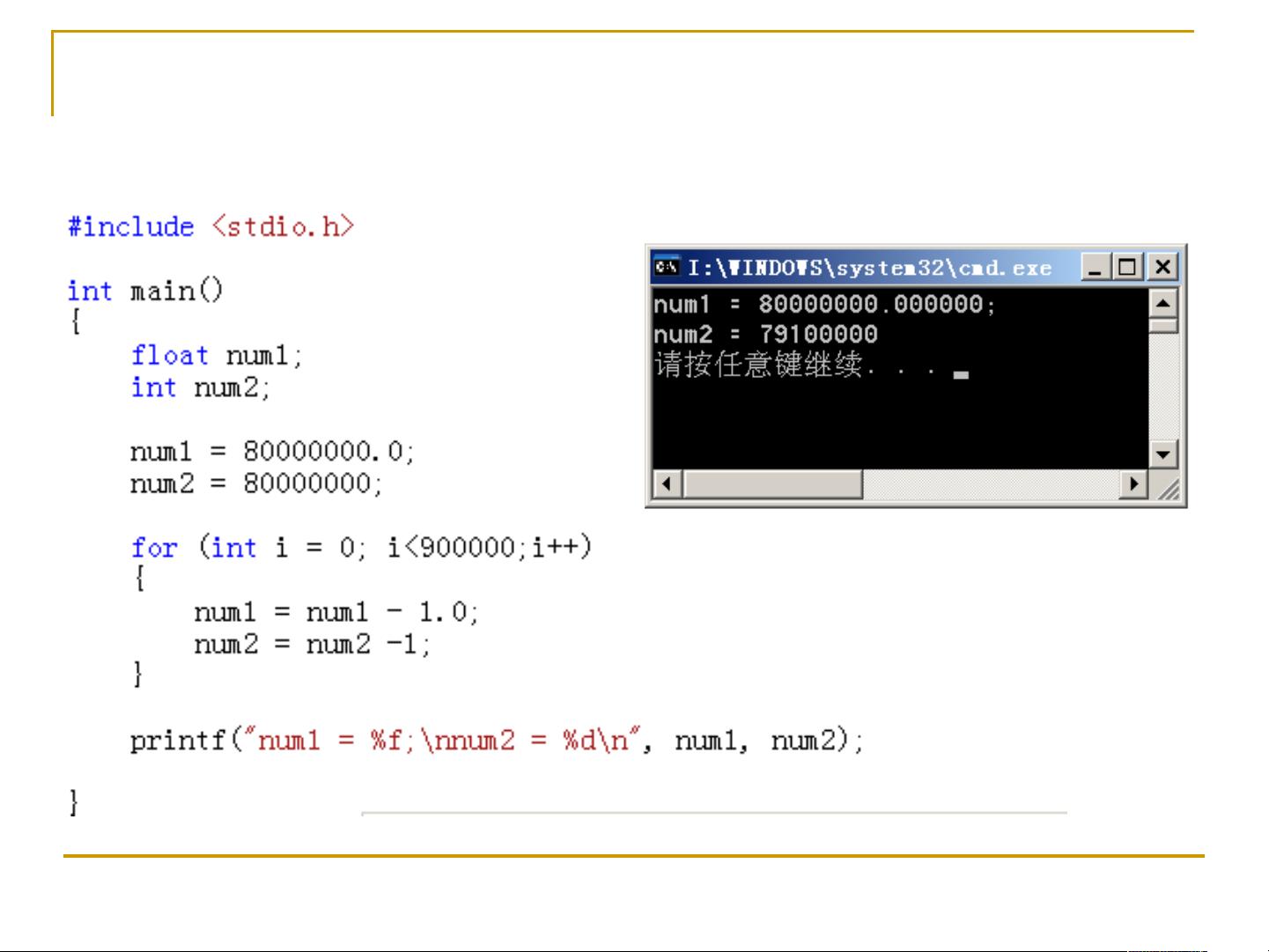
"算法复杂度的概念" 算法复杂度是计算机科学中一个非常重要的概念，它指的是一个算法在解决问题时所需要的计算资源和时间的增长趋势。算法复杂度是衡量一个算法优劣的重要指标。 在这里，我们将从算法复杂度的概念开始，讨论算法复杂度的定义、描述增长趋势的方法、算法复杂度的考察方法、算法复杂度的上界和下界、Fibonacci 数列问题的解决方法等。 算法复杂度是指问题随规模的增长算法所需消耗的运算时间和内存空间的增长趋势。因此，不考虑计算机本身硬件的特质，一般也忽略算法所消耗的与问题规模无关的固定量的计算与空间。 描述增长趋势的高低，可以使用大 O 表示法，即使用一个函数 f(n) 来描绘算法复杂度的上界的表示方式。记为：O（f(n)）。如果能同时找到算法复杂度的上下确界函数 g(n)和 f(n)，则算法复杂度能更精确的表达为 Θ(f(n))。 在算法复杂度的考察方法中，我们通常考察的是当问题复杂度 n 的增加时，运算所需时间、空间代价 f(n) 的上下界。进一步而言，又分为最好情况、平均情况、最坏情况三种情况。通常最坏情况往往是我们最关注的。 Fibonacci 数列问题是算法复杂度中一个非常重要的例子。 Fibonacci 数列是一个经典的递归序列，fib(n) = fib(n-1) + fib(n-2)，它的计算复杂度非常高。使用递归算法可以解决 Fibonacci 数列问题，但是它的计算复杂度非常高，时间复杂度为 O(2^n)。使用动态规划或矩阵表达法可以将计算复杂度降低到 O(n) 或 O(log n)。 算法复杂度的优化是非常重要的。在 Fibonacci 数列问题中，我们可以使用黄金分割数来优化算法复杂度，使得计算复杂度降低到 O(1.618^n)。此外，我们还可以使用双子星递归函数来实现该算法。 算法复杂度是一个非常重要的概念，它是衡量一个算法优劣的重要指标。了解算法复杂度的概念和描述增长趋势的方法对于算法设计和优化非常重要。