Adisciplinedapproachtoneuralnetworkhyper-parametersPartI资源-CSDN文库

需积分: 10 90 浏览量 2020-02-09 15:35:18 上传评论收藏 3.35MB PDF 举报

资源推荐

资源详情

资源评论

US Naval Research Laboratory Technical Report 5510-026

A DISCIPLINED APPROACH TO NEURAL NETWORK

HYPER-PARAMETERS: PART 1 – LEARNING RATE,

BATCH SIZE, MOMENTUM, AND WEIGHT DECAY

Leslie N. Smith

US Naval Research Laboratory

Washington, DC, USA

leslie.smith@nrl.navy.mil

ABSTRACT

Although deep learning has produced dazzling successes for applications of im-

age, speech, and video processing in the past few years, most trainings are with

suboptimal hyper-parameters, requiring unnecessarily long training times. Setting

the hyper-parameters remains a black art that requires years of experience to ac-

quire. This report proposes several efﬁcient ways to set the hyper-parameters that

signiﬁcantly reduce training time and improves performance. Speciﬁcally, this

report shows how to examine the training validation/test loss function for subtle

clues of underﬁtting and overﬁtting and suggests guidelines for moving toward

the optimal balance point. Then it discusses how to increase/decrease the learning

rate/momentum to speed up training. Our experiments show that it is crucial to

balance every manner of regularization for each dataset and architecture. Weight

decay is used as a sample regularizer to show how its optimal value is tightly

coupled with the learning rates and momentum. Files to help replicate the results

reported here are available at https://github.com/lnsmith54/hyperParam1.

1 INTRODUCTION

The rise of deep learning (DL) has the potential to transform our future as a human race even more

than it already has and perhaps more than any other technology. Deep learning has already created

signiﬁcant improvements in computer vision, speech recognition, and natural language processing,

which has led to deep learning based commercial products being ubiquitous in our society and in

our lives.

In spite of this success, the application of deep neural networks remains a black art, often requiring

years of experience to effectively choose optimal hyper-parameters, regularization, and network

architecture, which are all tightly coupled. Currently the process of setting the hyper-parameters,

including designing the network architecture, requires expertise and extensive trial and error and is

based more on serendipity than science. On the other hand, there is a recognized need to make the

application of deep learning as easy as possible.

Currently there are no simple and easy ways to set hyper-parameters – speciﬁcally, learning rate,

batch size, momentum, and weight decay. A grid search or random search (Bergstra & Bengio,

2012) of the hyper-parameter space is computationally expensive and time consuming. Yet train-

ing time and ﬁnal performance is highly dependent on good choices. In addition, practitioners

often choose one of the standard architectures (such as residual networks (He et al., 2016)) and the

hyper-parameter ﬁles that are freely available in a deep learning framework’s “model zoo” or from

github.com but these are often sub-optimal for the practitioner’s data.

This report proposes several methodologies for ﬁnding optimal settings for several hyper-

parameters. A comprehensive approach of all hyper-parameters is valuable due to the interdepen-

dence of all of these factors. Part 1 of this report examines learning rate, batch size, momentum, and

weight decay and Part 2 will examine the architecture, regularization, dataset and task. The goal is to

provide the practitioner with practical advice that saves time and effort, yet improves performance.

arXiv:1803.09820v2 [cs.LG] 24 Apr 2018

US Naval Research Laboratory Technical Report 5510-026

The basis of this approach is based on the well-known concept of the balance between underﬁtting

versus overﬁtting. Speciﬁcally, it consists of examining the training’s test/validation loss for clues of

underﬁtting and overﬁtting in order to strive for the optimal set of hyper-parameters (this report uses

“test loss” or “validation loss” interchangeably but both refer to use of validation data to ﬁnd the

error or accuracy produced by the network during training). This report also suggests paying close

attention to these clues while using cyclical learning rates (Smith, 2017) and cyclical momentum.

The experiments discussed herein indicate that the learning rate, momentum, and regularization are

tightly coupled and optimal values must be determined together.

Since this report is long, the reader who only wants the highlights of this report can: (1) look at

every Figure and caption, (2) read the paragraphs that start with Remark, and (2) review the hyper-

parameter checklist at the beginning of Section 5.

2 RELATED WORK

The topics discussed in this report are related to a great deal of the deep learning literature. See

Goodfellow et al. (2016) for an introductory text on the ﬁeld. Perhaps most related to this work is

the book “Neural networks: tricks of the trade” (Orr & M

uller, 2003) that contains several chapters

with practical advice on hyper-parameters, such as Bengio (2012). Hence, this section only discusses

a few of the most relevant papers.

This work builds on earlier work by the author. In particular, cyclical learning rates were introduced

by Smith (2015) and later updated in Smith (2017). Section 4.1 provides updated experiments on

super-convergence (Smith & Topin, 2017). There is a discussion in the literature on modifying the

batch size instead of the learning rate, such as discussed in Smith et al. (2017).

Several recent papers discuss the use of large learning rate and small batch size, such as Jastrzebski

et al. (2017a;b); Xing et al. (2018). They demonstrate that the ratio of the learning rate over the batch

size guides training. The recommendations in this report differs from those papers on the optimal

setting of learning rates and batch sizes.

Smith and Le (Smith & Le, 2017) explore batch sizes and correlate the optimal batch size to the

learning rate, size of the dataset, and momentum. This report is more comprehensive and more

practical in its focus. In addition, Section 4.2 recommends a larger batch size than this paper.

A recent paper questions the use of regularization by weight decay and dropout (Hern

andez-Garc

ıa

& K

onig, 2018). One of the ﬁndings of this report is that the total regularization needs to be in

balance for a given dataset and architecture. Our experiments suggest that their perspective on regu-

larization is limited – they only add regularization by data augmentation to replace the regularization

by weight decay and dropout without a full study of regularization.

There also exist approaches to learn optimal hyper-parameters by differentiating the gradient with

respect to the hyper-parameters (for example see Lorraine & Duvenaud (2018)). The approach in

this report is simpler for the practitioner to perform.

3 THE UNREASONABLE EFFECTIVENESS OF VALIDATION/TEST LOSS

“Well begun is half done.” Aristotle

A good detective observes subtle clues that the less observant miss. The purpose of this Section is

to draw your attention to the clues in the training process and provide guidance as to their meaning.

Often overlooked elements from the training process tell a story. By observing and understanding the

clues available early during training, we can tune our architecture and hyper-parameters with short

runs of a few epochs (an epoch is deﬁned as once through the entire training data). In particular,

by monitoring validation/test loss early in the training, enough information is available to tune the

architecture and hyper-parameters and this eliminates the necessity of running complete grid or

random searches.

Figure 1a shows plots of the training loss, validation accuracy, and validation loss for a learning rate

range test of a residual network on the Cifar dataset to ﬁnd reasonable learning rates for training.

In this situation, the test loss within the black box indicates signs of overﬁtting at learning rates

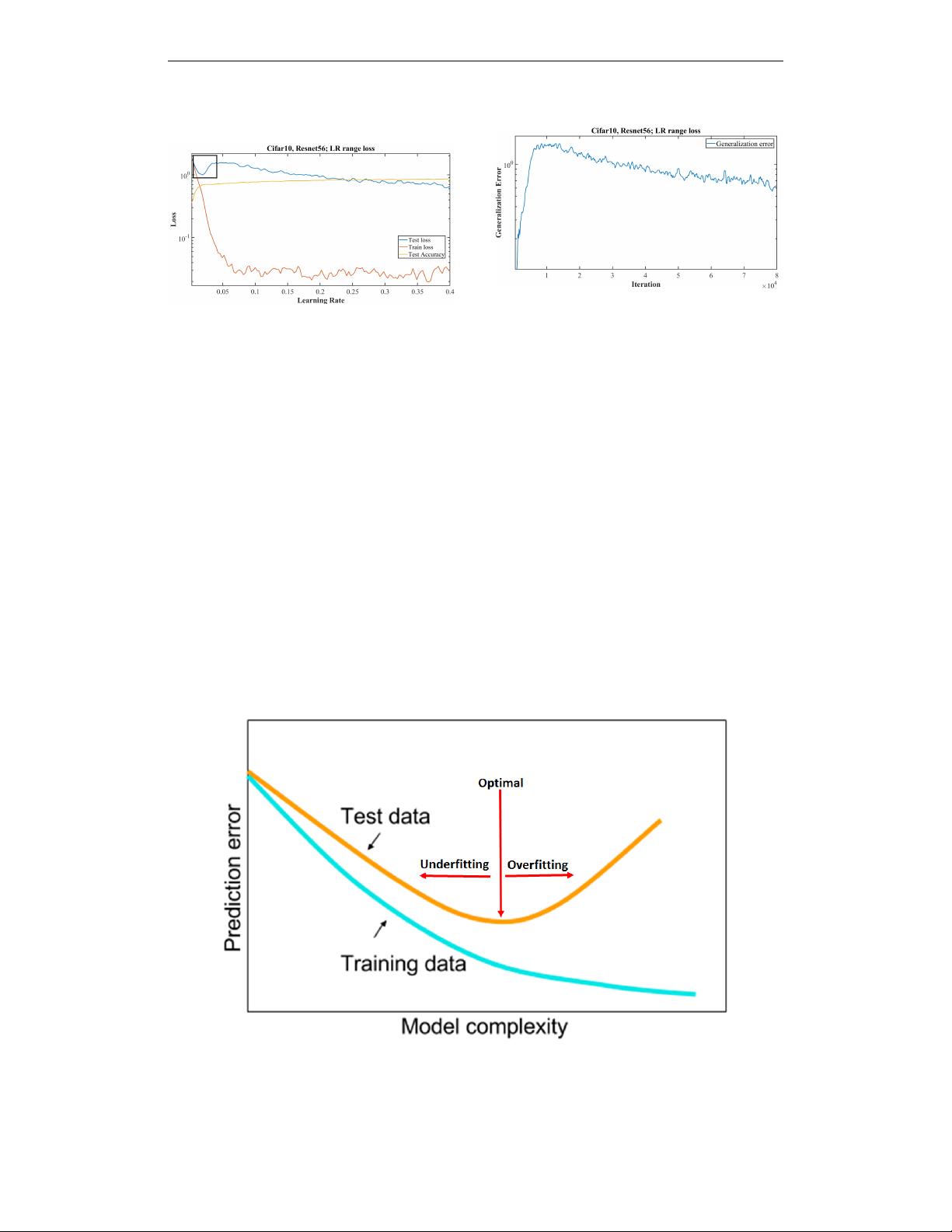
US Naval Research Laboratory Technical Report 5510-026

3.1 A REVIEW OF THE UNDERFITTING AND OVERFITTING TRADE-OFF

Underﬁtting is when the machine learning model is unable to reduce the error for either the test or

training set. The cause of underﬁtting is an under capacity of the machine learning model; that is,

it is not powerful enough to ﬁt the underlying complexities of the data distributions. Overﬁtting

happens when the machine learning model is so powerful as to ﬁt the training set too well and

the generalization error increases. The representation of this underﬁtting and overﬁtting trade-off

displayed in Figure 2, which implies that achieving a horizontal test loss can point the way to the

optimal balance point. Similarly, examining the test loss during the training of a network can also

point to the optimal balance of the hyper-parameters.

Remark 2. The takeaway is that achieving the horizontal part of the test loss is the goal of hyper-

parameter tuning. Achieving this balance can be difﬁcult with deep neural networks. Deep networks

are very powerful, with networks becoming more powerful with greater depth (i.e., more layers),

width (i.e, more neurons or ﬁlters per layer), and the addition of skip connections to the architecture.

Also, there are various forms of regulation, such as weight decay or dropout (Srivastava et al., 2014).

One needs to vary important hyper-parameters and can use a variety of optimization methods, such

as Nesterov or Adam (Kingma & Ba, 2014). It is well known that optimizing all of these elements

to achieve the best performance on a given dataset is a challenge.

An insight that inspired this Section is that signs of underﬁtting or overﬁtting of the test or validation

loss early in the training process are useful for tuning the hyper-parameters. This section started with

the quote “Well begun is half done” because substantial time can be saved by attending to the test

loss early in the training. For example, Figure 1a shows some overﬁtting within the black square

that indicates a sub-optimal choice of hyper-parameters. If the hyper-parameters are set well at the

beginning, they will perform well through the entire training process. In addition, if the hyper-

parameters are set using only a few epochs, a signiﬁcant time savings is possible in the search for

hyper-parameters. The test loss during the training process can be used to ﬁnd the optimal network

architecture and hyper-parameters without performing a full training in order to compare the ﬁnal

performance results.

The rest of this report discusses the early signs of underﬁtting and overﬁtting that are visible in the

test loss. In addition, it discusses how adjustments to the hyper-parameters affects underﬁtting and

overﬁtting. This is necessary in order to know how to adjust the hyper-parameters.

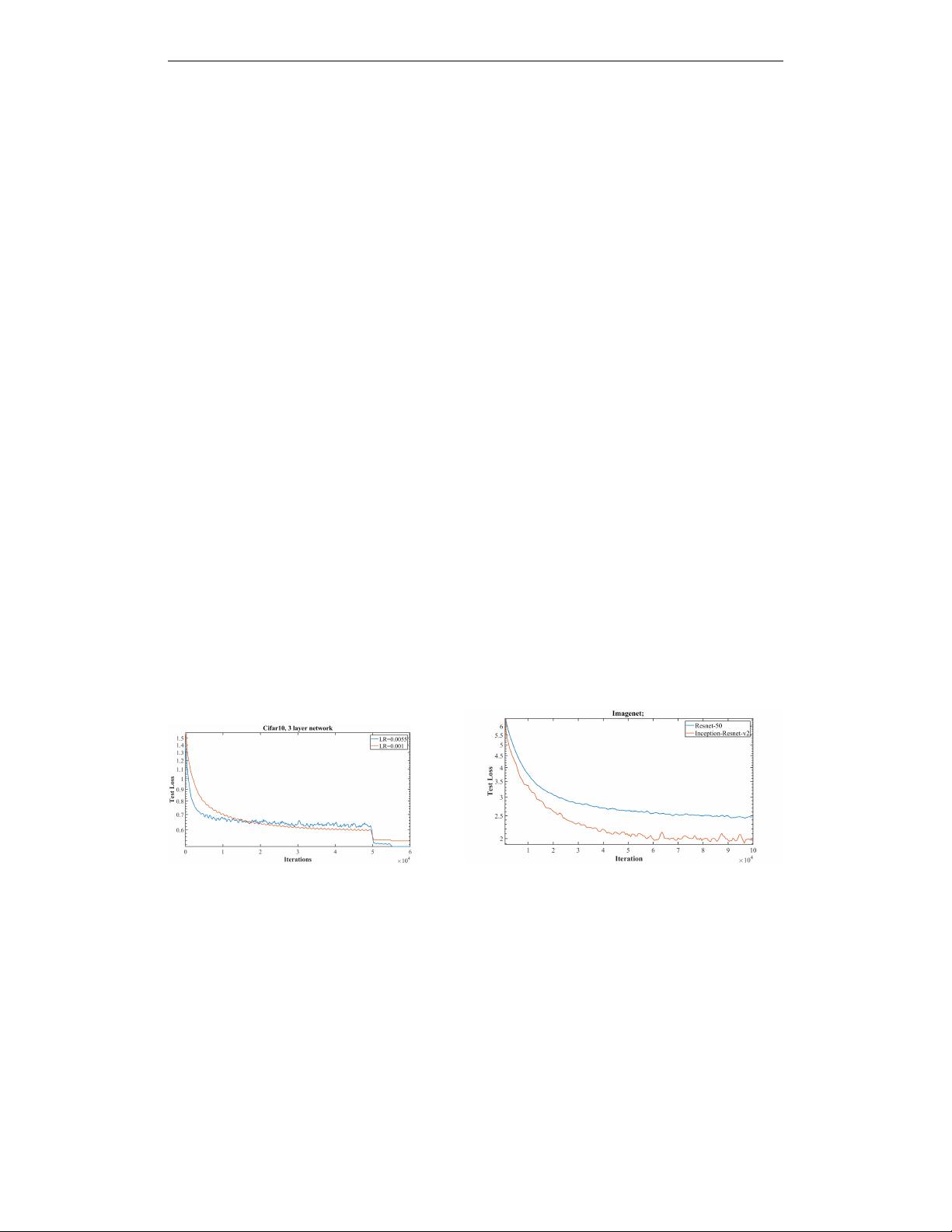
(a) Test loss for the Cifar-10 dataset with a

shallow 3 layer network.

(b) Test loss for Imagenet with two networks; resnet-50

and inception-resnet-v2.

Figure 3: Underﬁtting is characterized by a continuously decreasing test loss, rather than a horizontal

plateau. Underﬁtting is visible during the training on two different datasets, Cifar-10 and imagenet.

3.2 UNDERFITTING

Our ﬁrst example is with a shallow, 3-layer network on the Cifar-10 dataset. The red curve in Figure

3a with a learning rate of 0.001 shows a decreasing test loss. This curve indicates underﬁtting

because it continues to decrease, like the left side of the test loss curve in Figure 2. Increasing the

learning rate moves the training from underﬁtting towards overﬁtting. The blue curve shows the test

loss with a learning rate of 0.004. Note that the test loss decreases more rapidly during the initial

iterations and is then horizontal. This is one of the early positive clues that indicates that this curve’s

conﬁguration will produce a better ﬁnal accuracy than the other conﬁguration, which it does.

剩余20页未读，继续阅读

评论收藏

内容反馈

大饼博士X

粉丝: 4091
资源: 9

A disciplined approach to neural network hyper-parameters Part I

最新资源

A disciplined approach to neural network hyper-parameters Part I

神经网络算法

pytorch.cyclic.learning.rate:使用CLR算法进行训练（https

Designing Software Architectures - A Practical Approach

Software.Application.Development.A.Visual.Cplusplus.MFC.and.STL

IEEE-SWEBOK-2004

Software Application Development - A Visual C++ MFC and STL Tutorial

Object- Oriented Programming with Ansi-C

UML and the Unified Process.pdf

A MATLAB system for disciplined convex programming.zip

NIST SP800-175A.pdf

The Art of Designing Embedded Systems, 2nd. Edition

Disciplined Agile Delivery

NIST SP800-171.pdf

Convex.jl, disciplined凸规划的Julia包.zip

疯狂复试英语口语句型

ddc, Disciplined的弟子编译器.zip

Adaptive temperature compensation of GPS disciplined quartz and rubidium oscillators

Disciplined.AF-crx插件

Manning Java Reflection In Action

学位英语作文万能模版.doc

[4] 学位英语：核心词汇（四）.doc

21-must-read-books-for-your-summer-holiday.pdf

软件工程复习题-ans.doc

英文简历常用词汇集锦

最新资源