
IEEE TRANSACTIONS ON EVOLUTIONARY COMPUTATION, VOL. 1, NO. 1, APRIL 1997 53
Ant Colony System: A Cooperative Learning
Approach to the Traveling Salesman Problem
Marco Dorigo, Senior Member, IEEE, and Luca Maria Gambardella, Member, IEEE
Abstract—This paper introduces the ant colony system (ACS),
a distributed algorithm that is applied to the traveling salesman
problem (TSP). In the ACS, a set of cooperating agents called ants
cooperate to find good solutions to TSP’s. Ants cooperate using an
indirect form of communication mediated by a pheromone they
deposit on the edges of the TSP graph while building solutions.
We study the ACS by running experiments to understand its
operation. The results show that the ACS outperforms other
nature-inspired algorithms such as simulated annealing and evo-
lutionary computation, and we conclude comparing ACS-3-opt,
a version of the ACS augmented with a local search procedure,
to some of the best performing algorithms for symmetric and
asymmetric TSP’s.
Index Terms—Adaptive behavior, ant colony, emergent behav-
ior, traveling salesman problem.
I. INTRODUCTION
T
HE natural metaphor on which ant algorithms are based
is that of ant colonies. Real ants are capable of finding the
shortest path from a food source to their nest [3], [22] without
using visual cues [24] by exploiting pheromone information.
While walking, ants deposit pheromone on the ground and
follow, in probability, pheromone previously deposited by
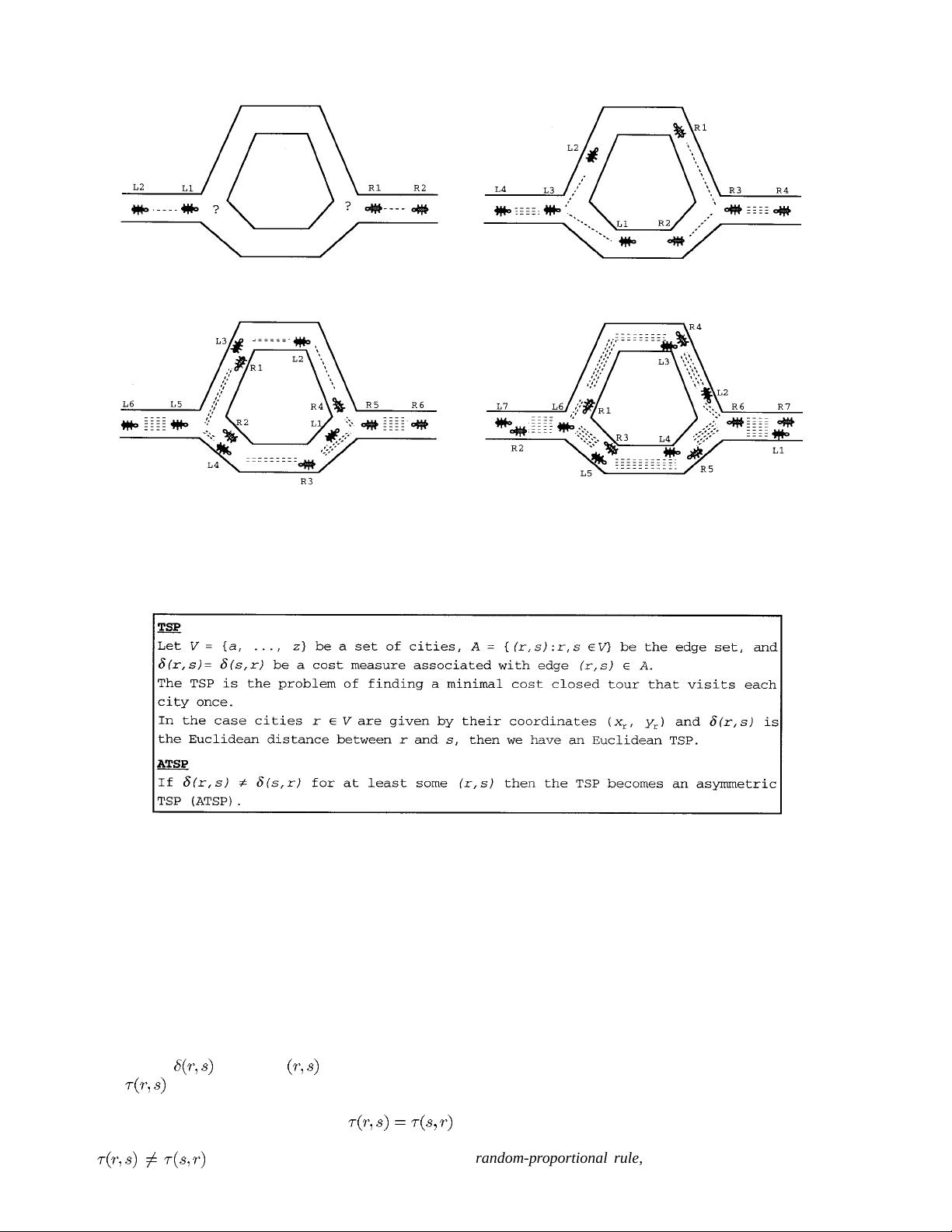
other ants. In Fig. 1, we show a way ants exploit pheromone
to find a shortest path between two points.
Consider Fig. 1(a): ants arrive at a decision point in which
they have to decide whether to turn left or right. Since they
have no clue about which is the best choice, they choose
randomly. It can be expected that, on average, half of the
ants decide to turn left and the other half to turn right. This
happens both to ants moving from left to right (those whose
name begins with an L) and to those moving from right to left
(name begins with an R). Fig. 1(b) and (c) shows what happens
in the immediately following instants, supposing that all ants
walk at approximately the same speed. The number of dashed
lines is roughly proportional to the amount of pheromone that
the ants have deposited on the ground. Since the lower path is
shorter than the upper one, more ants will visit it on average,
and therefore pheromone accumulates faster. After a short
transitory period the difference in the amount of pheromone
on the two paths is sufficiently large so as to influence the
decision of new ants coming into the system [this is shown by
Manuscript received October 7, 1996; revised January 18, 1997 and
February 3, 1997. This work was supported by the Swiss National Science
Fund Contract 21-45 653.95.
M. Dorigo is with IRIDIA, Universit
`
e Libre de Bruxelles, 1050 Bruxelles,
Belgium (e-mail: mdorigo@ulb.ac.be).
L. M. Gambardella is with IDSIA, 6900 Lugano, Switzerland.
Publisher Item Identifier S 1089-778X(97)03303-1.
Fig. 1(d)]. From now on, new ants will prefer in probability to
choose the lower path, since at the decision point they perceive
a greater amount of pheromone on the lower path. This in turn
increases, with a positive feedback effect, the number of ants
choosing the lower, and shorter, path. Very soon all ants will
be using the shorter path.
The above behavior of real ants has inspired ant system,
an algorithm in which a set of artificial ants cooperate to
the solution of a problem by exchanging information via
pheromone deposited on graph edges. The ant system has been
applied to combinatorial optimization problems such as the
traveling salesman problem (TSP) [7], [8], [10], [12] and the
quadratic assignment problem [32], [42].
The ant colony system (ACS), the algorithm presented
in this article, builds on the previous ant system in the
direction of improving efficiency when applied to symmetric
and asymmetric TSP’s. The main idea is that of having a set
of agents, called ants, search in parallel for good solutions to
the TSP and cooperate through pheromone-mediated indirect
and global communication. Informally, each ant constructs
a TSP solution in an iterative way: it adds new cities to a
partial solution by exploiting both information gained from
past experience and a greedy heuristic. Memory takes the form
of pheromone deposited by ants on TSP edges, while heuristic
information is simply given by the edge’s length.
The main novel idea introduced by ant algorithms, which
will be discussed in the remainder of the paper, is the syner-
gistic use of cooperation among many relatively simple agents
which communicate by distributed memory implemented as
pheromone deposited on edges of a graph.
This paper is organized as follows. Section II puts the
ACS in context by describing ant system, the progenitor
of the ACS. Section III introduces the ACS. Section IV is
dedicated to the study of some characteristics of the ACS:
We study how pheromone changes at run time, estimate the
optimal number of ants to be used, observe the effects of
pheromone-mediated cooperation, and evaluate the role that
pheromone and the greedy heuristic have in ACS performance.
Section V provides an overview of results on a set of standard
test problems and comparisons of the ACS with well-known
general purpose algorithms like evolutionary computation and
simulated annealing. In Section VI we add local optimization
to the ACS, obtaining a new algorithm called ACS-3-opt. This
algorithm is compared favorably with the winner of the First
International Contest on Evolutionary Optimization [5] on
asymmetric TSP (ATSP) problems (see Fig. 2), while it yields
a slightly worse performance on TSP problems. Section VII is
1089–778X/97$10.00 1997 IEEE



 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助 
 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜

 信息提交成功
信息提交成功