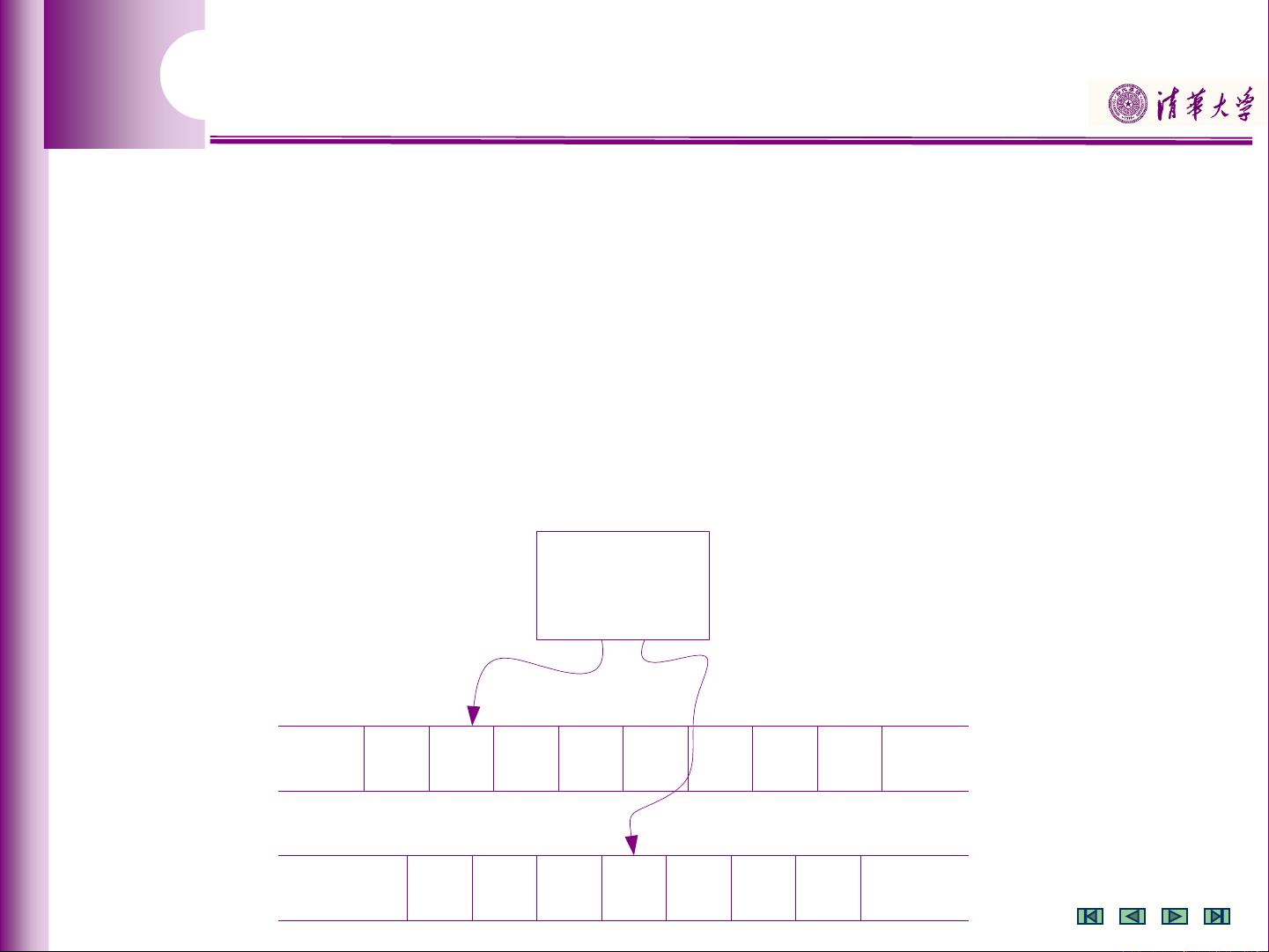
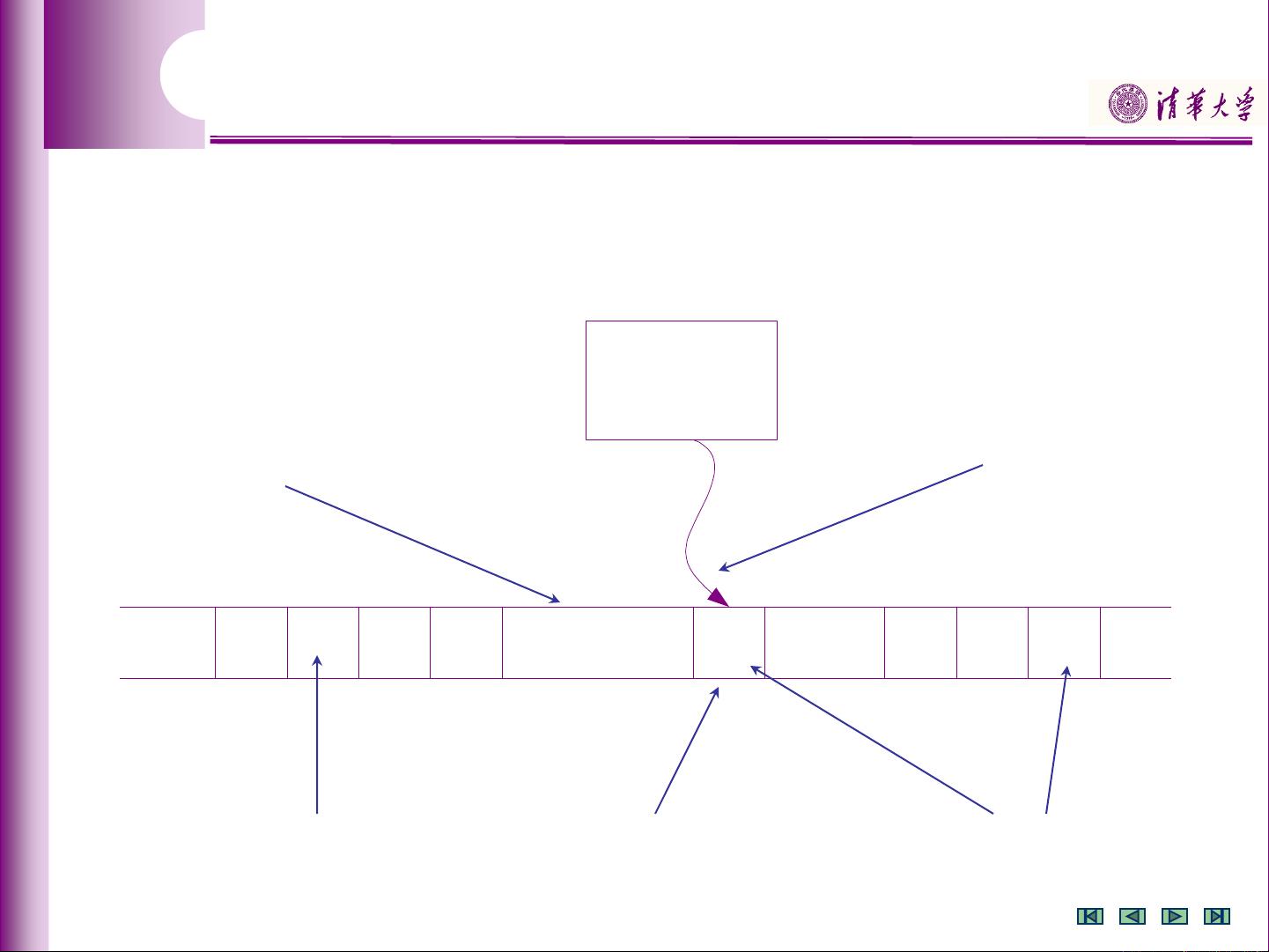
图灵机与递归可枚举语言
在形式语言与自动机理论中，图灵机是一个基本概念，用于描述计算机科学中最基本的计算模型。图灵机的概念与定义是指，图灵机是一个七元组，包括状态集、输入符号集、带符号集、转移函数、初始状态、特殊带符和终态集合。图灵机可以接受语言L = {0n1n2n | n ≥ 1}。
在形式语言与自动机理论中，递归可枚举语言是一个重要概念，指的是可以被图灵机接受的语言。递归可枚举语言的定义是，存在一个图灵机M，使得语言L = {0n1n2n | n ≥ 1}可以被M接受。
本节将详细介绍图灵机的概念与定义、递归可枚举语言的概念与定义，并通过实例讲解图灵机的工作原理和递归可枚举语言的应用。
图灵机的概念与定义
图灵机是一个七元组，包括状态集、输入符号集、带符号集、转移函数、初始状态、特殊带符和终态集合。状态集Q是一个有限集，输入符号集Σ是一个有限集，带符号集Γ是一个有限集，转移函数δ是一个偏函数，初始状态q0是一个状态，特殊带符B是一个特殊符号，终态集合F是一个状态集。
图灵机的七元组形式定义为：M = (Q, Σ, Γ, δ, q0, B, F)。
递归可枚举语言的概念与定义
递归可枚举语言是一个重要概念，指的是可以被图灵机接受的语言。递归可枚举语言的定义是，存在一个图灵机M，使得语言L可以被M接受。
在形式语言与自动机理论中，递归可枚举语言是指可以被图灵机接受的语言，例如语言L = {0n1n2n | n ≥ 1}是递归可枚举语言，因为存在一个图灵机M，使得语言L可以被M接受。
实例讲解
例如，设 language L = {0n1n2n | n ≥ 1}，可以构造一个图灵机M，使得语言L可以被M接受。图灵机M的七元组形式为：M = ({q0, q1, q2, q3, q4, q5, q6}, {0, 1, 2}, {0, 1, 2, X, Y, Z, B}, δ, q0, B, {q6})。
转移函数δ可以由转移图形式给出。例如，状态q1可以转移到状态q2，当输入符号为X时，带符号为Y，并将带符号Y移动到右边。
图灵机的工作原理
图灵机的工作原理是通过转移函数δ来实现的。转移函数δ将当前状态、输入符号和带符号作为输入，并输出新的状态、带符号和移动方向。例如，状态q1可以转移到状态q2，当输入符号为X时，带符号为Y，并将带符号Y移动到右边。
递归可枚举语言的应用
递归可枚举语言在计算机科学中有广泛应用，例如在编译器设计、自然语言处理、人工智能等领域。递归可枚举语言可以用于描述计算机语言的语法结构，并用于实现编译器、解释器等。
图灵机和递归可枚举语言是形式语言与自动机理论中的基本概念，它们之间存在紧密的联系，图灵机可以接受递归可枚举语言，并且递归可枚举语言可以被图灵机接受。
