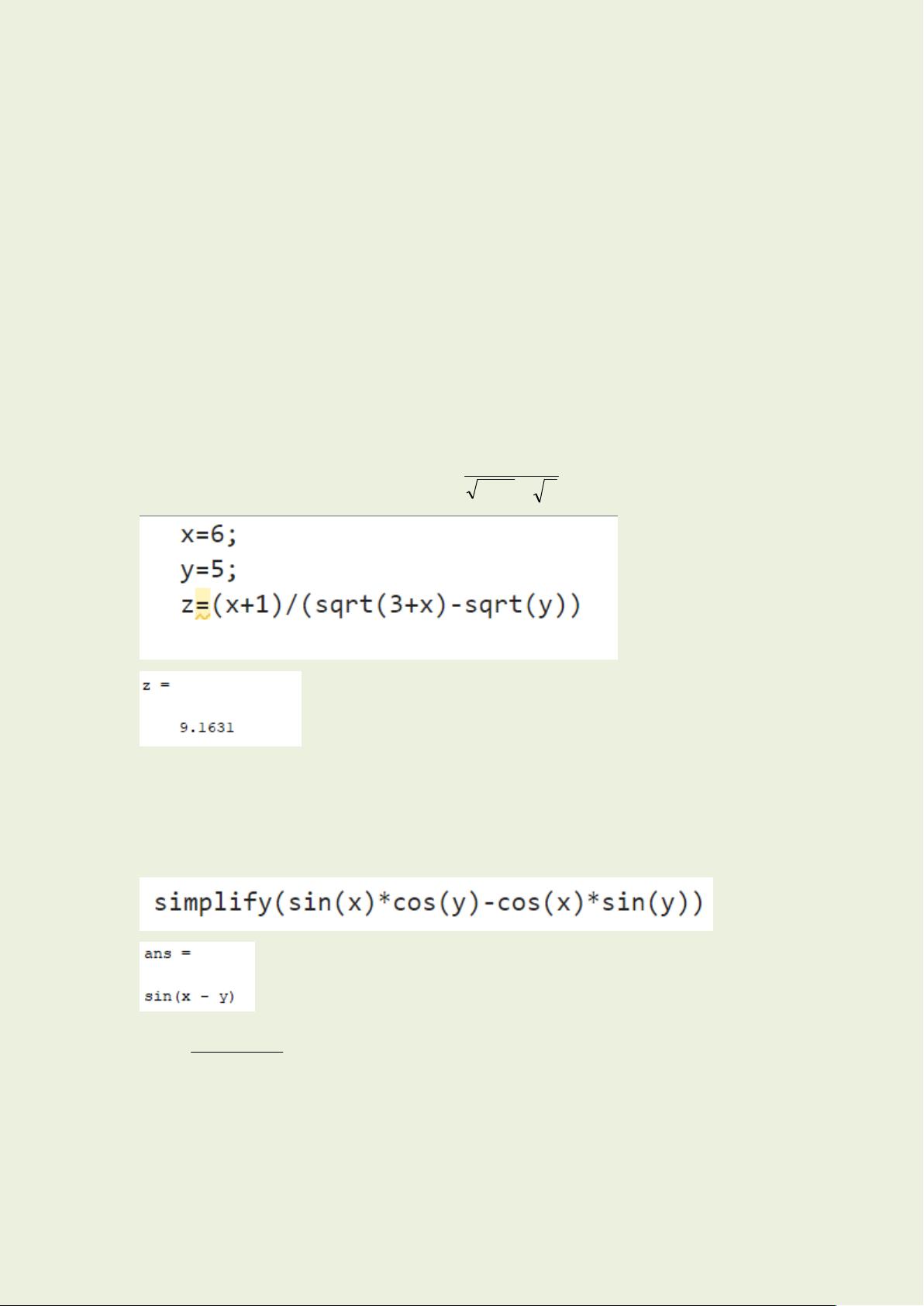
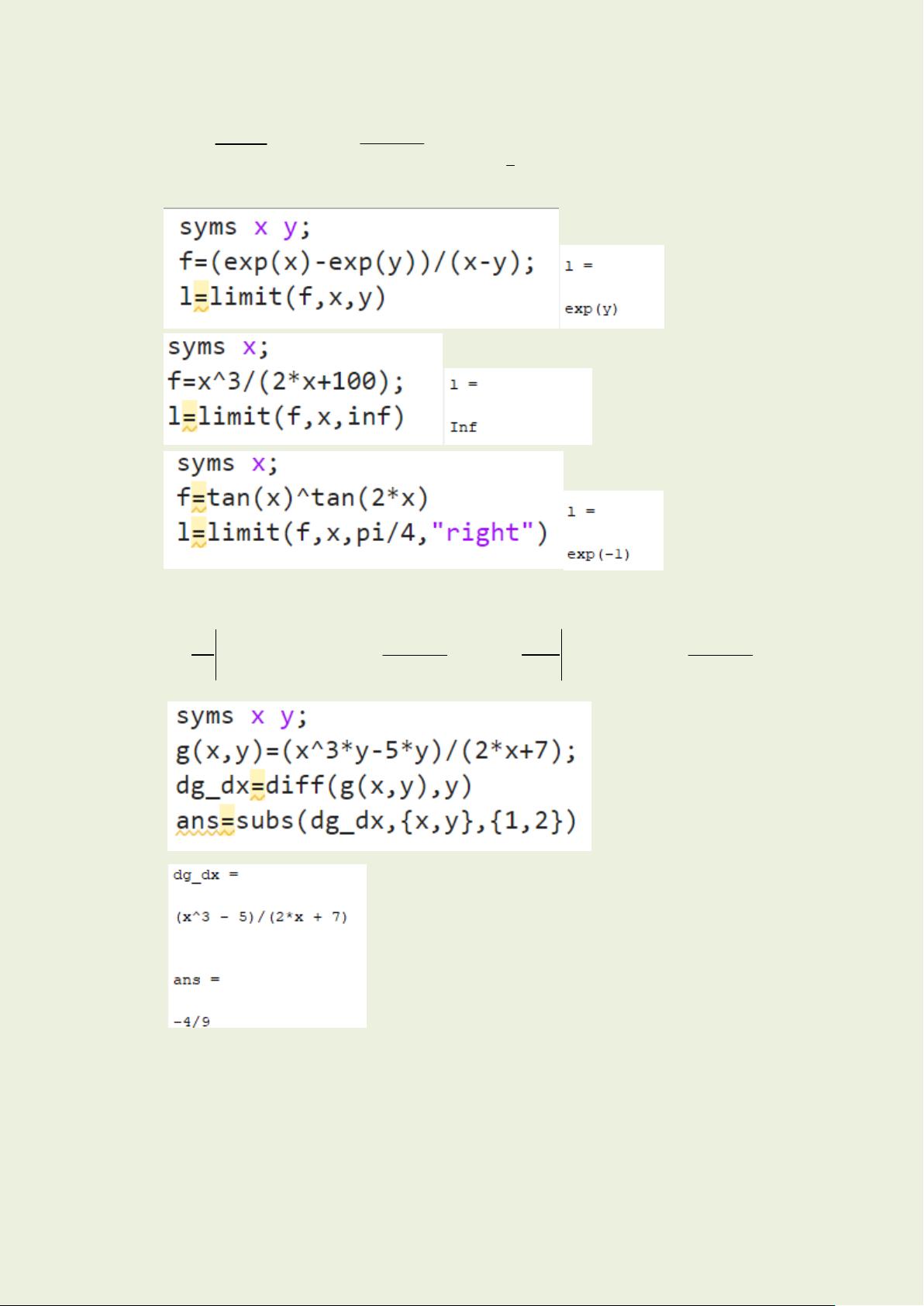
### MATLAB实验三四综合应用知识点详解
#### 一、实验目的
本实验旨在通过一系列实践操作，帮助学习者深入了解MATLAB中的符号计算功能及其在解决数学问题中的应用。具体包括：
1. **掌握定义符号对象的方法**：理解如何在MATLAB中创建符号变量，并基于这些变量构建复杂的数学表达式。
2. **掌握符号表达式的运算法则以及符号矩阵运算**：学会使用MATLAB内置的函数来简化、展开或因式分解表达式，并进行符号矩阵的加减乘除等运算。
3. **掌握求符号函数极限及导数的方法**：了解如何使用MATLAB来计算函数的极限和导数，这对于理解和分析函数的性质非常重要。
4. **掌握求符号函数定积分和不定积分的方法**：掌握如何在MATLAB中求解函数的定积分和不定积分，这对于计算面积、体积等问题非常有用。
5. **掌握求级数求和和Taylor级数**：学会使用MATLAB来计算无穷级数的和，并了解如何使用Taylor级数近似函数。
6. **了解采用数值计算与符号计算求解线性方程组的区别**：对比两种不同的方法在求解线性方程组时的特点与优劣。
#### 二、实验内容解析
1. **已知x=6,y=5，利用符号表达式求\(y \cdot x^{3} / z\)**
- **实现步骤**：
1. 定义符号变量`x`, `y`, `z`。
2. 将`x`和`y`赋值为具体的数字。
3. 构建表达式`y * x^3 / z`。
4. 对表达式进行简化，并将结果输出为数值形式。
2. **化简表达式**
- **表达式1**: \(2 \cdot \sin^2(c) - \cos^2(c)\)
- **表达式2**: \(12x^3 - 8x^2 + 4x - 2\)
- **实现步骤**：
1. 定义符号变量`c`和`x`。
2. 构建表达式，并使用MATLAB内置函数如`simplify()`进行化简。
3. **矩阵运算**
- **给定矩阵**：
- \(A = \begin{bmatrix} h & g & f \\ e & d & c \\ a & b & P \end{bmatrix}\),
- \(P_1 = \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \end{bmatrix}\),
- \(P_2 = \begin{bmatrix} 1 & 0 & 1 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{bmatrix}\).
- **实现步骤**：
1. 定义矩阵`A`, `P1`, `P2`。
2. 计算`B = P1 * P2 * A`。
4. **复合函数及其导数**
- **复合函数**: \(u = \ln(v), v = e^{-x}, u = \ln(e^{-x}) = -x\)。
- **实现步骤**：
1. 定义符号变量`x`。
2. 构建复合函数`u`。
3. 使用`diff()`函数求导。
5. **求极限**
- **极限1**: \(\lim_{x \to y} \frac{e^x - e^y}{x - y}\)。
- **极限2**: \(\lim_{x \to +\infty} \frac{x^3 + 2x + 1}{x^2 + 1}\)。
- **极限3**: \(\lim_{x \to \pi/4} \frac{\tan(x) - 1}{x - \pi/4}\)。
- **实现步骤**：
1. 定义符号变量`x`和`y`。
2. 构建极限表达式，并使用`limit()`函数求极限。
6. **求导数**
- **导数1**: 已知\(g(x, y) = \frac{3y^2 + 5}{27x^2 + y}\)，求\(\frac{dg}{dx}\)。
- **导数2**: 已知\(f(x) = \sin(x) \cdot \log(x) \cdot e^{1/x}\)，求\(\frac{df}{dx}\)。
- **实现步骤**：
1. 定义符号变量`x`和`y`。
2. 构建函数表达式。
3. 使用`diff()`函数求导。
7. **求积分**
- **积分1**: \(\int \frac{1}{x + 1} dx\)。
- **积分2**: \(\int_{0}^{1} \frac{1}{x + 1} dx\)。
- **积分3**: \(\int_{0}^{1} \frac{t}{x + 1} dx\)。
- **积分4**: \(\int_{-\infty}^{\infty} \frac{\sin(y)}{x^2 \cdot y + 1} dy\)。
- **积分5**: \(\iint_{-\infty}^{\infty} \frac{\sin(y)}{x^2 \cdot y + 1} dy dx\)。
- **实现步骤**：
1. 定义符号变量`x`、`y`和`t`。
2. 构建积分表达式，并使用`int()`函数求积分。
8. **求级数的和**
- **级数1**: \(\sum_{k=1}^{n} k^3\)。
- **级数2**: \(\sum_{k=1}^{\infty} \frac{1}{k^2}\)。
- **级数3**: \(\sum_{k=1}^{\infty} k \cdot x^k\)。
- **实现步骤**：
1. 定义符号变量`k`和`x`。
2. 构建级数表达式，并使用`symsum()`函数求和。
9. **Taylor级数**
- **函数**: \(f(x) = e^x\)。
- **实现步骤**：
1. 定义符号变量`x`。
2. 构建函数表达式。
3. 使用`taylor()`函数求Taylor级数。
10. **积分中值定理验证**
- **验证公式**: 寻找\((0,1)\)内的一个值\(x\)，使得\(\int_{0}^{1} \frac{1}{(x + 1)^2} dx = \frac{1}{(x + 1)^2}\)。
- **实现步骤**：
1. 定义函数\(f(x) = \frac{1}{(x + 1)^2}\)。
2. 计算积分\(\int_{0}^{1} f(x) dx\)。
3. 使用`solve()`函数求解方程\(f(x) = \text{积分值}\)。
11. **线性方程组求解**
- **方程组1**:
\[
\left\{
\begin{aligned}
2x_1 - 2x_2 + 3x_3 &= 5 \\
-x_1 + x_2 - 2x_3 &= 3 \\
2x_1 - 3x_2 + x_3 &= 0
\end{aligned}
\right.
\]
- **方程组2**:
\[
\left\{
\begin{aligned}
2x_1 - 2x_2 + 3x_3 &= 5 \\
-x_1 + x_2 - 2x_3 &= 3 \\
2x_1 - 3x_2 + x_3 &= 8
\end{aligned}
\right.
\]
- **实现步骤**：
1. 定义符号变量`x1`, `x2`, `x3`。
2. 构建方程组表达式。
3. 使用`solve()`函数求解方程组。
#### 三、总结
通过以上实验内容的学习与实践，我们不仅掌握了MATLAB中符号计算的基本操作方法，还深入理解了如何运用这些工具解决复杂的数学问题。符号计算相比于数值计算，在求解过程中更加精确，能够提供准确的解析解，这对于理论研究和深入理解数学概念具有重要意义。同时，MATLAB提供的强大功能使得这一过程变得相对简单直观，极大地提高了学习效率。
