【线性规划基础概念】
线性规划是一种优化方法,用于在一组线性约束条件下最大化或最小化一个线性目标函数。在本PPT学习教案中,我们关注的是如何解决简单的线性规划问题。
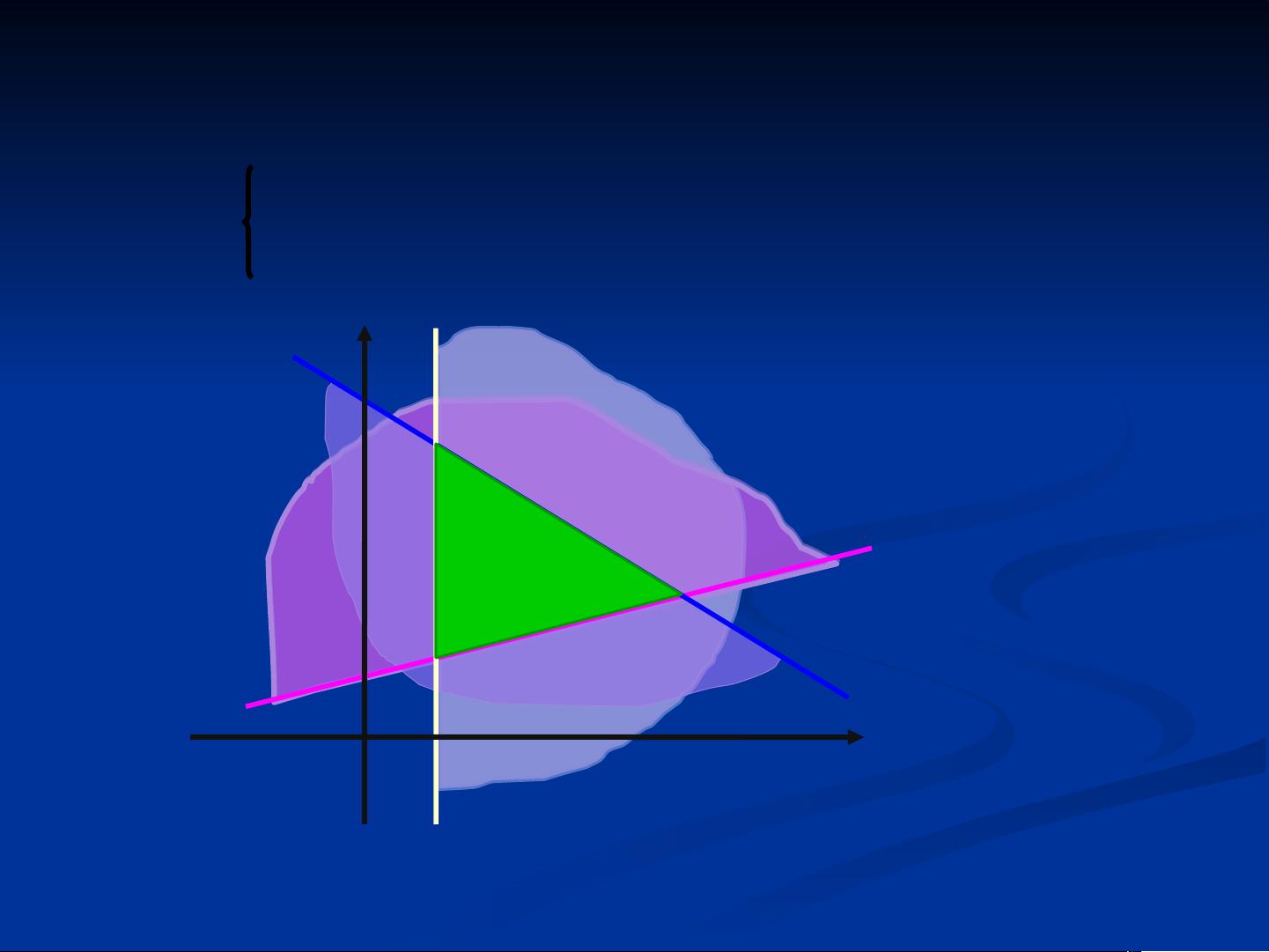
1. **线性不等式组与可行域**:
约束条件通常由线性不等式组成,例如3x + 5y ≤ 25, x - 4y ≤ -3, 和 x ≥ 1。这些不等式在二维坐标系中形成一个封闭的区域,称为可行域。可行域是所有满足所有约束条件的点(x, y)的集合。
2. **目标函数与最优解**:
目标函数是我们希望最大化或最小化的表达式,例如z = 2x + y。在案例中,我们寻找z的最大值和最小值。最优解是指使得目标函数达到最大值或最小值的可行解。
3. **平面区域的分析**:
分析平面区域的形状和边界可以帮助我们理解目标函数的行为。例如,x = 1是一条垂直线,而3x + 5y = 25和x - 4y = -3分别代表斜率为-3/5和4的直线。
4. **几何意义**:
目标函数z = 2x + y可以看作是斜率为-2的直线族。通过平移这条直线,我们可以观察z值的变化。当直线移动到可行域的边界上时,z值达到最大或最小。
5. **找到最优解**:
解决线性规划问题通常包括以下步骤:
a. **画出可行域**:根据给定的线性不等式画出可行域。
b. **平移目标函数**:将目标函数表示为一组平行线,然后平移找到与可行域相交且截距最大或最小的线。
c. **解方程组**:确定这些交点的坐标,通过解方程组来得到。
d. **得出最优解**:交点坐标就是最优解,对应的z值即为最大值或最小值。
例如,在案例中,当2x - y = z过点A(5, 2)时,z取得最大值12;而当它过点B(1, 1)时,z取得最小值3。
6. **线性约束条件与线性目标函数**:
约束条件是由x和y的一次不等式或方程组成的,目标函数则是一次解析式,如z = ax + by。如果目标函数和约束条件都是线性的,那么问题被称为线性规划。
7. **可行解与可行域**:
可行解是满足所有线性约束的(x, y)点,可行域是所有这些点的集合。这个集合可能是闭合的或者开的,可以是凸的或者非凸的,但在这个简单的例子中,它是闭合的并且凸的。
通过理解和应用这些基本概念,我们可以有效地解决线性规划问题,找到在特定限制下最优的决策方案。在实际的会计学或其他领域,线性规划常用于资源分配、成本最小化或收益最大化等问题。