微波遥感52PPT学习教案.pptx

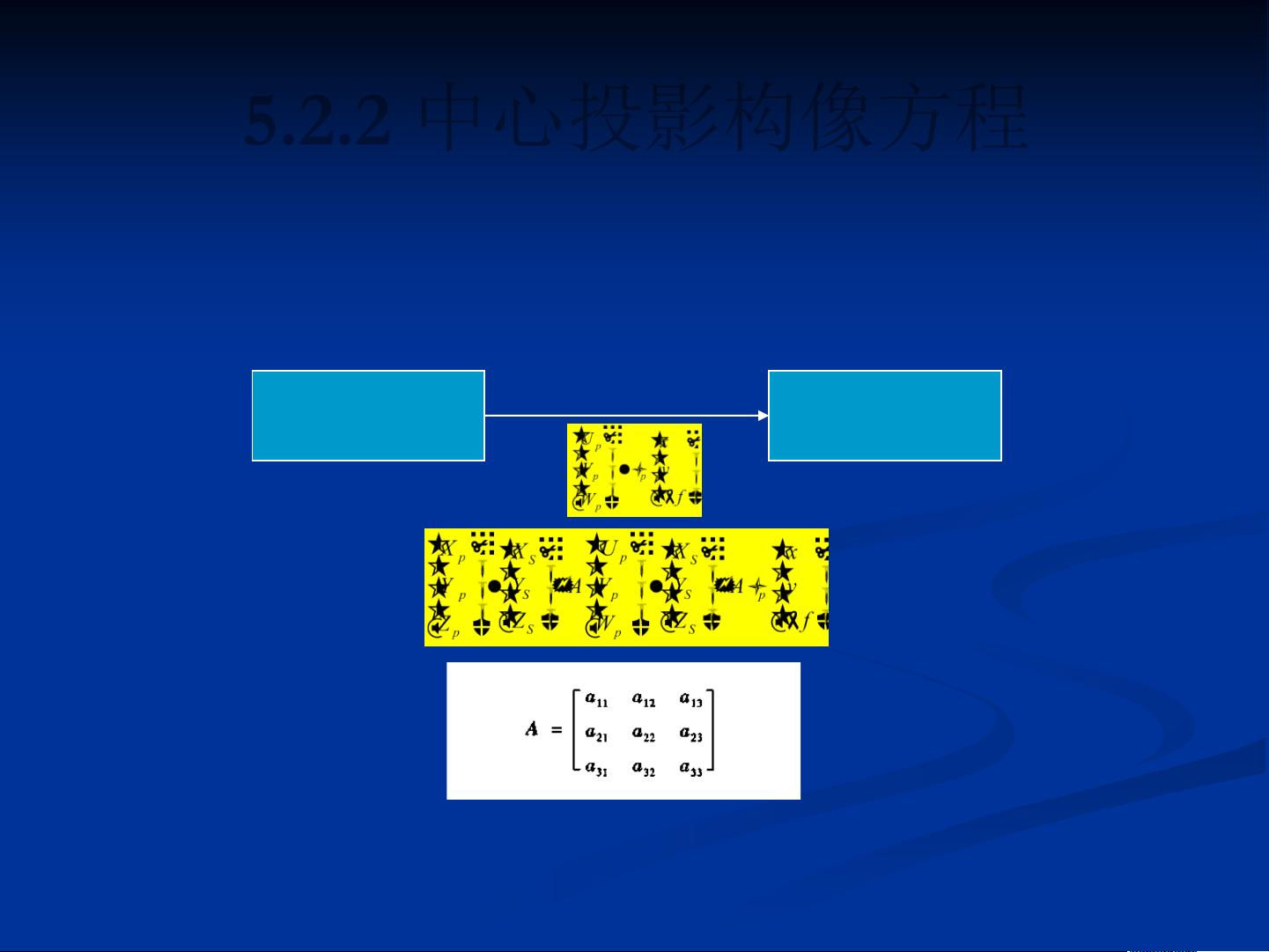
微波遥感是一种重要的地球观测技术，通过分析不同波段的微波辐射，可以获取地表的各种信息，如地形、植被覆盖、土壤湿度等。在遥感领域，图像的成像过程是理解数据的关键，而构像方程则是描述这个过程的数学工具。 构像方程是将图像坐标（x, y）与大地坐标（X, Y, Z）之间关联的数学表达式，它描述了从三维空间中的地表点到二维图像平面上像点的投影关系。通常，构像方程涉及到多个坐标系，包括传感器坐标系（S-UVW）、像点坐标系（o-xyf）、地面坐标系（O-XYZ）以及地图坐标系（Om-XmYm）。这些坐标系之间的转换关系确保了空间信息的准确传递。 5.2.2 中心投影构像方程描述的是像点坐标（x, y, -f）与传感器坐标（U, V, W）的关系，它简化了地表点到像点的投影过程，通常用于框幅式相机的成像。反算公式和最简形式的共线方程是解决实际问题时的常用工具，用于计算未知点的位置或反求相机的外方位元素。 5.2.3 全景摄影机的构像方程适用于旋转式相机，如全景相机，其特点是像点P的投影中心随每一点的变化而变化，像空间坐标s-uvw与地表坐标O-XYZ之间的关系由曝光缝隙等效画幅式像片来描述。 5.2.4 推扫式传感器的构像方程则适应于卫星遥感器等扫描成像设备，每个像元的投影中心都不同，因此几何关系更复杂，但依然遵循类似的中心投影原理。 5.2.5 扫描式传感器的构像方程则进一步考虑了传感器在扫描过程中连续采集数据的特点，每个像素的形成与扫描速度和时间有关。 5.2.6 侧视雷达的构像方程则涉及到了雷达的工作原理，雷达通过发射和接收回波来确定目标的位置和特性，侧视雷达的成像过程与上述有所不同，因为它涉及到射频信号的传播和散射。 5.2.7 改进的侧视雷达共线条件方程引入了等效中心投影的概念，以更好地处理雷达图像的几何校正问题。内外方位元素在此方程中起到关键作用，它们分别描述了像点与物点的相对位置和相机的姿态信息。 5.2.8 基于多项式模型的传感器校正是遥感图像处理中的重要步骤，通过拟合多项式函数，可以校正传感器成像过程中产生的几何失真，提高图像的质量和分析精度。 总结来说，微波遥感的构像方程理论涵盖了从简单到复杂的各种成像情况，包括中心投影、全景、推扫和扫描式传感器以及侧视雷达。这些方程和模型对于理解和处理遥感数据至关重要，特别是在进行图像校正和地理定位时。通过深入学习和理解这些概念，可以提高遥感数据分析的准确性和可靠性。