基于C++的g2o优化算法库设计源码分析资源-CSDN文库

共698个文件

h：279个

cpp：272个

txt：80个

版权申诉

源码分析

优化算法

13 浏览量 2024-10-04 18:38:26 上传评论收藏 4.67MB ZIP 举报

资源推荐

资源详情

资源评论

收起资源包目录

基于C++的g2o优化算法库设计源码分析（698个子文件）

install-deps-windows.bat 952B

robots.bib 2KB

os_specific.c 2KB

.clang-format 6KB

android.toolchain.cmake 80KB

FindBLAS.cmake 42KB

FindLAPACK.cmake 10KB

FindEigen3.cmake 3KB

FindG2O.cmake 3KB

FindSuiteSparse.cmake 3KB

CheckIfUnderscorePrefixedBesselFunctionsExist.cmake 3KB

FindCholmod.cmake 2KB

FindQGLViewer.cmake 1KB

FindCSparse.cmake 618B

doxy.config 74KB

COPYING 1KB

freeglut_stroke_mono_roman.cpp 47KB

freeglut_stroke_roman.cpp 47KB

flex_scanner.cpp 46KB

sparse_system_helper.cpp 40KB

g2o-unfold.cpp 34KB

bison_parser.cpp 33KB

g2o.cpp 26KB

optimizable_graph.cpp 26KB

g2o_hierarchical.cpp 21KB

sparse_optimizer.cpp 20KB

graph_optimizer_sparse_incremental.cpp 20KB

graph_operations.cpp 20KB

simple_star_ops.cpp 17KB

simulator_3d_plane.cpp 16KB

main_window.cpp 15KB

sclam_pure_calibration.cpp 15KB

g2o_slam_interface.cpp 14KB

base_fixed_sized_edge.cpp 13KB

bal_example.cpp 13KB

simulator_3d_line.cpp 12KB

command_args.cpp 12KB

simulator.cpp 12KB

ba_anchored_inverse_depth_demo.cpp 11KB

types_icp.cpp 10KB

sba_demo.cpp 10KB

hyper_dijkstra.cpp 10KB

sclam_odom_laser.cpp 10KB

convertSegmentLine.cpp 10KB

estimate_propagator.cpp 10KB

generate_commands.cpp 10KB

jacobian_timing_tests.cpp 10KB

auto_diff.cpp 10KB

hyper_graph_action.cpp 9KB

gm2dl_io.cpp 9KB

graph_optimizer_sparse_online.cpp 9KB

ba_demo.cpp 9KB

edge_labeler.cpp 9KB

static_dynamic_function_fit.cpp 9KB

test_simulator2d.cpp 9KB

simulator2d_segment.cpp 9KB

optimization_algorithm_dogleg.cpp 8KB

solver_slam2d_linear.cpp 8KB

opengl_primitives.cpp 8KB

dquat2mat_maxima_generated.cpp 8KB

create_sphere.cpp 8KB

test_simulator3d.cpp 8KB

gicp_sba_demo.cpp 8KB

solver_cholmod.cpp 8KB

jacobians_slam3d.cpp 8KB

marginal_covariance_cholesky.cpp 7KB

closed_form_calibration.cpp 7KB

types_seven_dof_expmap.cpp 7KB

io_slam3d.cpp 7KB

edge_se2.cpp 7KB

edge_se3_pointxyz_disparity.cpp 7KB

output_helper.cpp 7KB

polynomial_fit.cpp 7KB

circle_fit.cpp 7KB

hyper_graph.cpp 7KB

edge_project_p2sc.cpp 7KB

g2o_incremental.cpp 7KB

edge_se3_lotsofxyz.cpp 7KB

edge_se3_pointxyz.cpp 6KB

sclam_laser_calib.cpp 6KB

edge_se2_lotsofxy.cpp 6KB

constant_velocity_target.cpp 6KB

optimization_algorithm_levenberg.cpp 6KB

linear_solver_test.cpp 6KB

factory.cpp 6KB

robot_laser.cpp 6KB

edge_line2d_pointxy.cpp 6KB

edge_se3.cpp 6KB

edge_se2_pointxy.cpp 6KB

g2o_hierarchical_test_functions.cpp 6KB

edge_se2_segment2d.cpp 6KB

edge_se2_line2d.cpp 6KB

slam2d_viewer.cpp 6KB

solver_eigen.cpp 6KB

tutorial_slam2d.cpp 6KB

robust_kernel_impl.cpp 6KB

optimize_sphere_by_sim3.cpp 6KB

tictoc.cpp 6KB

curve_fit.cpp 6KB

gicp_demo.cpp 6KB

共 698 条

o: A general Framework for (Hyper) Graph Optimization

Giorgio Grisetti, Rainer K¨ummerle, Hauke Strasdat, Kurt Konolige

email: {grisetti,kuemmerl}@informatik.uni-freiburg.de

strasdat@gmail.com konolige@willowgarage.com

March 11, 2017

In this document we describe a C++ framework for performing the optimization of nonlinear least

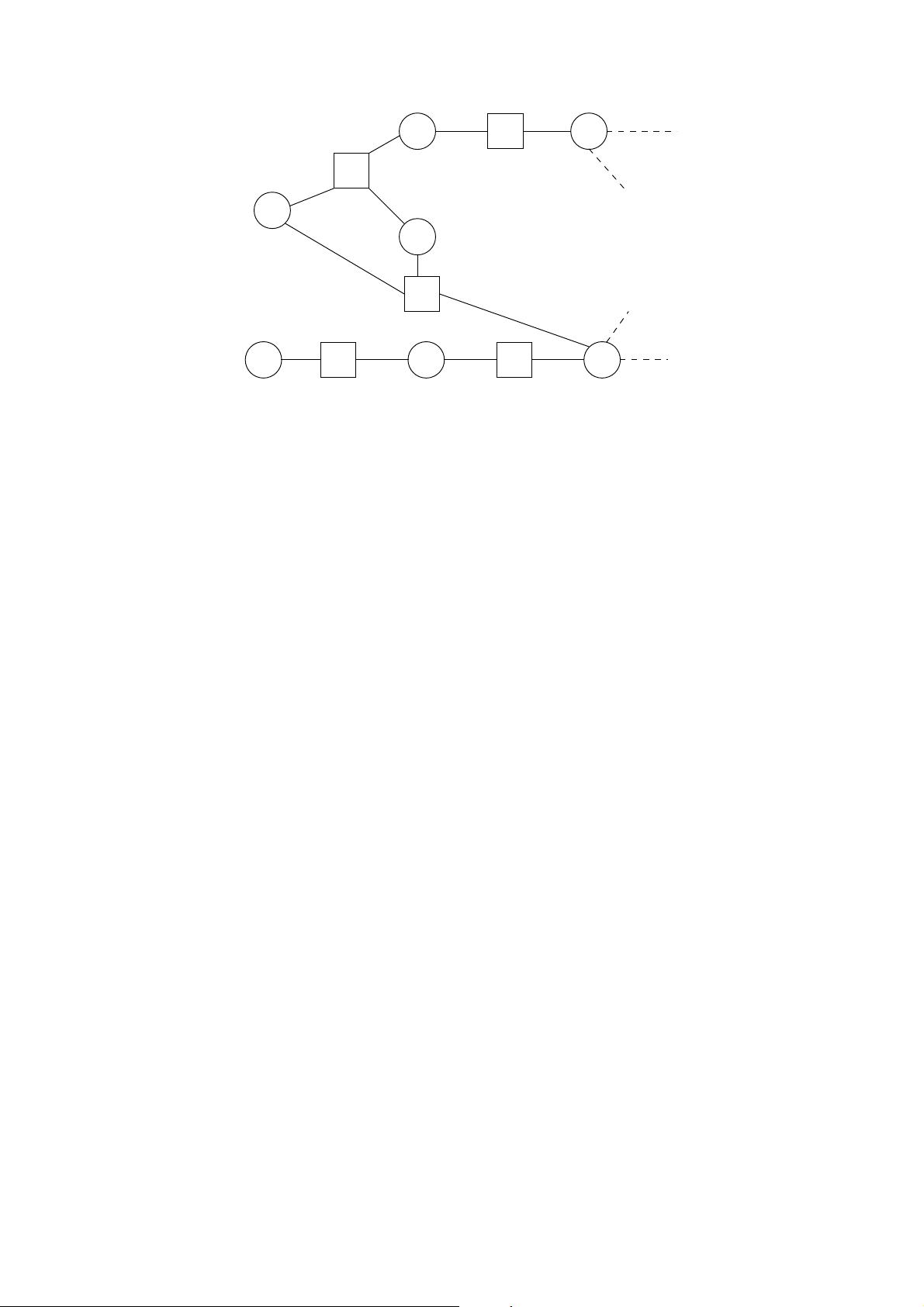
squares problems that can be embedded as a graph or in a hyper-graph. A hyper-graph is an extension

of a graph where an edge can connect multiple nod e s and not only two. Several problems in robotics and

in computer vision require to ﬁnd the optimum of an error function with respect of a set of parameter s .

Examples include, popular applications like SLAM and Bundle adjustment.

In the literature, many approaches have been proposed to address this class of problems. The naive

implementation of standard methods, like Levenberg-Marquardt or Gauss -Ne wton can lead to acceptable

results for most applications, when the correct parameterization is chosen. However, to achieve the

maximum performances substantial eﬀorts might b e required.

o stand s for General (Hyper) Graph Optimization. The purposes of this framework are the follow-

ing:

• To provide an easy-to-extend and easy-to-use general library for graph optimization that can be

easily applied to diﬀerent problems,

• To provide p eopl e who want to understand SLAM or BA with an easy-to-read implementation that

focuses on the relevant details of the problem speciﬁcation.

• Achieve state-of-the-art per for mance s , while being as general as possible.

In the remainder of this do cu ment we will ﬁrst characterize the (hyper) graph-embeddable problems,

and we will give an introduction to their solution via the popular Levenberg-Marquardt or Gauss-Newton

algorithms implemented in this library. Subsequently, we will describe the high-level behavior of the

library, and the basic structures. Finally, we will introduce how to implement 2D SLAM as a simple

example.

This document is not a replacement for the in-line do cu mentation. Instead, it is a d i gest

to help the user/reader to read/browse and extend the code.

Please cite this when using g

R. K¨ummerle, G. Gr is et ti , H. Strasdat, K. Konolige, and W. Burgard. g2o: A General Framework for

Graph Optimization. In Proc. of the IEEE Int. Conf. on Robotics an d Automation (ICRA). Shanghai,

China, May 2011.

1 (Hyper)Graph-Embe ddabl e Optimization Problems

A least squares minimization problem can be described by the following equation:

F(x) =

k∈C

, z

)

Ω

, z

)

{z }

(1)

∗

= argmin

F(x). (2)

i−1

Figure 1: This example illustrates how to represent an objective function by a hyp er -gr aph . Here we

illustrate a portion of a small SLAM problem [1]. In this example we assume that where the measurement

functions are governed by some unknown calibration parameters K. The robot poses are rep r e se nted by

the variables p

1:n

. These variables are connected by constraints z

depicted by the square boxes. The

constraints arise, for instance, by matching nearby laser scans in the laser reference frame. The relation

betwe en a laser match and a robot pose, however, depends on the position of the sensor on the robot,

which is mo de le d by the calibration parameters K. Conversely, subsequent robot poses are connected

by binary constraints u

arising from odometry measurements. These measur eme nts are made in the

frame of the robot mobile base.

Here

• x = (x

, . . . , x

)

is a vector of parameters, where each x

represents a generic parameter block.

• x

= (x

, . . . , x

)

⊂ (x

, . . . , x

)

is the subset of the parameters involved in the k

constraint.

• z

and Ω

represent r e spectively the mean and the information matrix of a constraint relating th e

parameters in x

• e

) is a vector error function that measures how well the parameter blocks in x

satisfy the

constraint z

. It is 0 when x

and x

perfectly match the constraint. As an example, if one has

a measurement function

= h

) that generates a synthetic measurement

given an actual

conﬁguration of the nodes in x

. A straightforward error function would then be e(x

, z

) =

) − z

For simplicity of notation, in the res t of this paper we will encode the measurement in the indices of the

error function:

, z

)

def.

= e

)

def.

= e

(x). (3)

Note that each parameter block and each error function can span over a diﬀerent space. A problem in

this form can be eﬀectively re p r es ented by a directed hyper-graph. A node i of the graph represe nts the

parameter block x

∈ x

and an hyper-edge among the nodes x

∈ x

represents a constraint involving all

nodes in x

. In case the hyper edges have size 2, the hyper-graph becomes an ordinary graph. Figure 1

shows an example of mapping between a hyp e r -gr aph and an objective function.

2 Least Squar es Optimization

If a good initial guess

x of the p ar ameter s is known, a numerical solution of Eq. 2 can be obtained by using

the popular Gauss-Newton or Levenberg-Marquardt algorithms [2, §15.5]. The idea is to approximate

the error function by its ﬁrst order Taylor expansion around the current initial guess

(

+ ∆x

) = e

(

x + ∆x) (4)

≃ e

+ J

∆x. (5)

Here J

is the Jacobian of e

(x) computed in

x and e

def.

= e

(

x). Substituting Eq. 5 in the error terms

of Eq. 1, we obtain

(

x + ∆x) (6)

= e

(

x + ∆x)

Ω

(

x + ∆x) (7)

≃ (e

+ J

∆x)

Ω

+ J

∆x) (8)

= e

Ω

{z }

+2 e

Ω

{z }

∆x + ∆x

Ω

{z }

∆x (9)

= c

+ 2b

∆x + ∆x

∆x (10)

With this local approximation, we can rewrite the function F(x) given in Eq. 1 as

x + ∆x) =

k∈C

(

x + ∆x) (11)

≃

k∈C

+ 2b

∆x + ∆x

∆x (12)

= c + 2b

∆x + ∆x

H∆x. (13)

The quadratic form i n Eq. 13 is obtained from Eq. 12 by setting c =

, b =

and H =

It can be minimized in ∆x by solving the linear system

H ∆x

∗

= −b. (14)

The matrix H is the information matrix of the system and is sparse by construction, having non-zeros only

betwe en blocks connected by a constraint. Its number of non-zero blocks is twice the number of constrains

plus the numbe r of no d es . This allows to solve Eq. 14 with eﬃcient approaches like sparse Cholesky

factorization or Preconditioned Conju gate Gradients (PCG). An highly eﬃcient implementation of sparse

Cholesky factorization can be found in publicly available packages like CSparse [3] or CHOLMOD [4].

The linearized soluti on is then obtained by adding to the initial guess the computed incre ments

∗

x + ∆x

∗

. (15)

The pop ular Gauss-Newton algorithm iterates the linearization in Eq. 13, the solu ti on in Eq. 14 and

the update step in Eq. 15. In every iteration, the prev ious solution is used as linearization point and as

initial guess.

The Levenberg-Marquardt (LM) algorithm is a nonlinear variant to Gauss-Newton that introduces

a damping factor and backup actions to control the convergence. Instead of solving directly Eq. 14 LM

solves a damped version of it

(H + λI) ∆x

∗

= −b. (16)

Here λ is a damping factor: the larger λ is the smaller are the ∆x. This is useful to control the step size

in case of non-linear surfaces. The idea behind the LM algorithm is to dynamically control the damping

factor. At each iteration the error of the n ew conﬁguration is monitored. If the new error is lower than

the previous one, lambda is decreased for the next iteration. Otherwise, the solution is reverted and

lambda is increased. For a more detailed explanation of the LM algorithm implemented in our package

we r ef er to [5].

The procedures described above are a general approach to multivariate function minimization. The

general appr oach, however, assumes that the space of parameters x is Euclidean, which is not valid

for several problems like SLAM or bundle adjustment. This may lead to su b- opti mal solutions. In

the remainder of this section we discuss ﬁrst the general solution when the space of the parameters i s

Euclidean, and sub s eq ue ntly we extend this solution to more general non-Euclidean spaces.

3 Considerations about the Structure of the Linearized System

According to Eq. 13, the matrix H and the vector b are obtained by summing up a set of matr ice s and

vectors, one for every constraint. If we set b

= J

Ω

and H

= J

Ω

we can rewrite H and b as

b =

k∈C

(17)

H =

k∈C

. (18)

Every cons tr aint will contribute to the system with an addend term. The structure of this adden d

depends on the Jacobian of the error function. Since the e r r or function of a constraint depends only on

the values of the nodes x

∈ x

, the Jacobian in Eq. 5 has the following form:



0 · · · 0 J

· · · J

· · · 0 · · · J

0 · · · 0



. (19)

Here J

∂e(x

)

∂x

are the derivatives of the error function with respect to the nodes connected by the

hyper-edge, with respect to the par amete r block x

∈ x

From Eq. 9 we obtain the following structure for the block matrix H







Ω

· · · J

Ω

· · · J

Ω

· · · J

Ω

· · · J

Ω

· · · J

Ω

· · · J

Ω







(20)







Ω







(21)

For simplicity of notation we omitte d the zero blocks. The reader might notice that the b lock structur e

of the matrix H is the adjacency matrix of the hyper graph. Additionally the Hessian H is a symmetric

matrix, since all th e H

are symmetric. A single hyper-edge connecting q vertices will introduce q

non

zero blocks in the Hessian, in correspondence of each pair



, x



, of nodes connected.

4 Least Squar es on Manifold

To deal with parameter blocks that s pan over a non-Euclidean spaces, it is common to ap ply the error

minimization on a manifold. A manifold is a mathematical space that is n ot necessarily Euclidean on a

global scale, but can be seen as Euclidean on a local scale [6].

For example, in the context of SLAM problem, each parameter block x

consists of a translation vector

and a rotational component α

. The translation t

clearly forms a Euclid ean sp ace. In contrast to that,

the rotational components α

span over the non-Euclidean 2D or 3D rotation group SO(2) or SO(3).

To avoid singularities, these spaces are usually described in an over-parameterized way, e.g., by rotation

matrices or quaternions. Directly applying Eq. 15 to these over-parameterized representations breaks

the constraints induced by the over-parameterization. The over-parameterization results in additional

degrees of fr e ed om and thus introduces errors in the solution. To overcome this problem, one can use

a minimal representation for the rotati on (like Euler angles in 3D). This, however, is the n subject to

singularities.

An alternative idea is to consider the underlying space as a manifold and to deﬁne an operator ⊞

that maps a local variation ∆x in t he Euclidean space to a variation on the manifold, ∆x 7→ x ⊞ ∆x.

We refer the reader to [7, §1.3] for more mathematical details. W it h this operator, a new error func ti on

can be deﬁned as

(∆˜x

)

def.

= e

(

⊞ ∆˜x

) (22)

= e

(

x ⊞ ∆˜x) ≃

∆˜x, (23)

where

x spans over the original over-parameterized space, for instance quaterni ons . The term ∆˜x

is a small increment around the original position

x and is expressed in a minimal representation. A

common choice for SO(3) is to use the vector part of the unit quaternion. In more detail, one can

represent the increments ∆˜x as 6D vectors ∆˜x

= (∆

˜q

), where ∆

t denotes the translation and

˜q

= (∆q

∆q

)

is the vector part of th e unit quaternion representing the 3D rotation. Conversely,

= (

) uses a quaternion

q to enc ode the r otational part. Thus, the operator ⊞ can be expressed

by ﬁrst converting ∆

q to a full quaternion ∆q and then applying t he transformation ∆x

= (∆t

∆q

)

x. In the equations describ in g the error minimization, these operations can nicely be encapsulated by

the ⊞ operator. The Jacobian

can be expres se d by

∂e

(

x ⊞ ∆˜x)

∂∆˜x



∆˜x=0

. (24)

Since in the previous equation

e depends only on ∆˜x

∈ ∆˜x

we can further expand it as follows:

∂e

(

x ⊞ ∆˜x)

∂∆˜x



∆˜x=0

(25)



0 · · · 0

· · ·

· · · 0 · · ·

0 · · · 0



. (26)

With a straightforward extens ion of notation, we se t

∂e

(

x ⊞ ∆˜x)

∂∆˜x



∆˜x=0

(27)

With a straightforward extension of the notation, we can insert Eq. 23 in Eq. 8 and Eq. 11. This

leads to the following increments:

H ∆˜x

∗

= −

b. (28)

Since the increments ∆˜x

∗

are computed in the local Euclidean surroundin gs of the initial guess

x, they

need to be re-mapped into the ori ginal redundant space by the ⊞ operator. Accordingly, the update rule

of Eq. 15 becomes

∗

x ⊞ ∆˜x

∗

. (29)

In summary, formalizing the minimization problem on a manifold consists of ﬁrst computing a se t of

increments in a local Eu cl id ean approximation around the in iti al guess by Eq. 28, and second accumulat-

ing the increments in the global non-Euclid ean space by Eq. 29. Note that the linear system computed

on a manifold representation has the same structure like the linear system computed on an Euclidean

space. One can easily derive a manifold version of a graph minimization from a non-manifold version,

only by deﬁning an ⊞ operator and its Jacobian

w.r.t. the corresponding parameter block. In g

we provide tools for numerically computing the Jacobians on the manifold space. This requires the user

to implement the error function and the ⊞ operator only. As a design choice, we do not address the

non-manifold case since it is already contained in the manifold one. However, to achieve the maximum

performances and accuracy we recommend the user to implement analytic Jacobians, once the system is

functioning with t he numeric ones.

评论收藏

内容反馈

版权申诉

wjs2024

粉丝: 2368
资源: 5478

基于C++的g2o优化算法库设计源码分析

基于C++语言的g2o优化算法设计源码分析

基于C++的g2o优化设计源码分析与应用

基于C++语言的g2o优化与扩展设计源码

基于C++的G2O图优化库设计源码

基于C++和C语言实现的g2o优化算法设计源码

基于C++和Shell的g2o增强型优化算法设计源码

基于C++语言开发的军旗游戏完整源码

基于C++的命令行linux文件管理系统源码.zip

基于C++的TCMalloc内存优化模块设计源码

基于C++的ATM机模拟程序系统源码.zip

基于Java语言的Jenetics遗传算法库设计源码

基于C++为一体机触控白板设计的课堂随机点名器源码.zip

基于c++的网卡流量数据包分析源码.zip

基于c++和Qt实现的扫雷游戏源码（c++程序设计）.zip

期末大作业课程设计基于C++的Qt框架开发的翻金币小游戏源码.zip

基于C++语言实现数字雨效果完整源码

C++实现基于GAlib遗传算法库解决TSP问题源码(含超详细注释+sln解决方案).zip

基于C++实现的餐厅自助点餐系统设计源码+项目说明（高分课设）.zip

基于C++语言实现的象棋源码

基于C++语言实现的播放器源码

基于C++的智能五子棋程序系统源码.zip

基于C++QT个人通讯录管理系统源码.zip

Visual C++实现的基因遗传算法库源代码以演示程序.zip

基于C++的地图导航系统设计与实现源码+PPT.zip

基于C和C++实现的嵌入式设备算法库(含PID控制器-哈夫曼编码器-哈希表-环形队列算法实现).zip

基于C++实现的低通滤波器源码（含FIR、IIR低通滤波器设计）.zip

基于C++语言的esp_dc1设计源码及跨平台兼容性优化方案

课程设计基于C++&QT的超市管理系统源码+文档说明（高分项目）

基于Qt+C++的CAD图形设计平台源码（毕业设计）

最新资源