Recovering High Dynamic Range Radiance Maps from Photographs
Paul E. Debevec Jitendra Malik
University of California at Berkeley
1
ABSTRACT
We present a method of recovering high dynamic range radiance
maps from photographs taken with conventional imaging equip-
ment. In our method, multiple photographs of the scene are taken
with different amounts of exposure. Our algorithm uses these dif-
ferently exposed photographs to recover the response function of the
imaging process, up to factor of scale, using the assumption of reci-
procity. With the known response function, the algorithm can fuse
the multiple photographs into a single, high dynamic range radiance
map whose pixel values are proportional to the true radiance values
in the scene. We demonstrate our method on images acquired with
both photochemical and digital imaging processes. We discuss how
this work is applicable in many areas of computer graphics involv-
ing digitized photographs, including image-based modeling, image
compositing, and image processing. Lastly, we demonstrate a few
applications of having high dynamic range radiance maps, such as
synthesizing realistic motion blur and simulating the response of the
human visual system.
CR Descriptors: I.2.10 [Artificial Intelligence]: Vision and
Scene Understanding - Intensity, color, photometry and threshold-
ing; I.3.7 [ComputerGraphics]: Three-Dimensional Graphics and
Realism - Color, shading, shadowing, and texture; I.4.1 [Image
Processing]: Digitization - Scanning; I.4.8 [Image Processing]:
Scene Analysis - Photometry, Sensor Fusion.
1 Introduction
Digitized photographs are becoming increasingly important in com-
puter graphics. More than ever, scanned images are used as texture
maps for geometric models, and recent work in image-based mod-
eling and rendering uses images as the fundamental modeling prim-
itive. Furthermore, many of today’s graphics applications require
computer-generated images to mesh seamlessly with real photo-
graphic imagery. Properly using photographically acquired imagery
in these applications can greatly benefit from an accurate model of
the photographic process.
When we photograph a scene, either with film or an elec-
tronic imaging array, and digitize the photograph to obtain a two-
dimensional array of “brightness” values, these values are rarely
1
Computer Science Division, University of California at Berkeley,
Berkeley, CA 94720-1776. Email: debevec@cs.berkeley.edu, ma-
lik@cs.berkeley.edu. More information and additional results may be found
at: http://www.cs.berkeley.edu/˜debevec/Research
true measurements of relative radiance in the scene. For example, if
one pixel has twice the value of another, it is unlikely that it observed
twice the radiance. Instead, there is usually an unknown, nonlinear
mapping that determines how radiance in the scene becomes pixel
values in the image.
This nonlinear mapping is hard to know beforehand because it is
actually the composition of several nonlinear mappings that occur
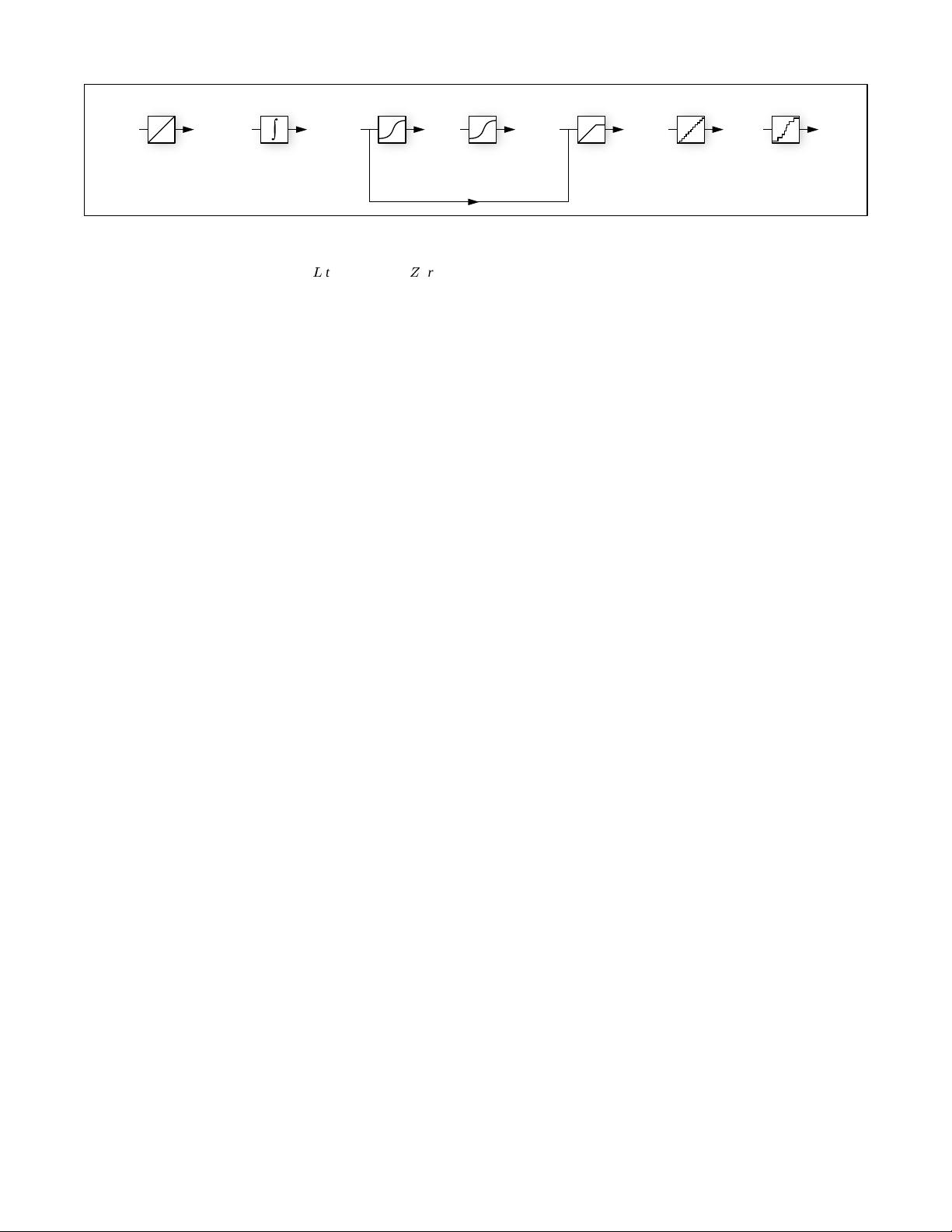
in the photographic process. In a conventional camera (see Fig. 1),
the film is first exposed to light to form a latent image. The film is
then developed to change this latent image into variations in trans-
parency, or density, on the film. The film can then be digitized using
a film scanner, which projects light through the film onto an elec-
tronic light-sensitive array, converting the image to electrical volt-
ages. These voltages are digitized, and then manipulated before fi-
nally being written to the storage medium. If prints of the film are
scanned rather than the film itself, then the printing process can also
introduce nonlinear mappings.
In the first stage of the process, the film response to variations
in exposure
X
(which is
E
t
, the product of the irradiance
E
the
film receives and the exposure time
t
) is a non-linear function,
called the “characteristic curve” of the film. Noteworthy in the typ-
ical characteristic curve is the presence of a small response with no
exposure and saturation at high exposures. The development, scan-
ning and digitization processes usually introduce their own nonlin-
earities which compose to give the aggregate nonlinear relationship
between the image pixel exposures
X
and their values
Z
.
Digital cameras, which use charge coupled device (CCD) arrays
to image the scene, are prone to the same difficulties. Although the
charge collected by a CCD element is proportional to its irradiance,
most digital cameras apply a nonlinear mapping to the CCD outputs
before they are written to the storage medium. This nonlinear map-
ping is used in various ways to mimic the response characteristics of
film, anticipate nonlinear responses in the display device, and often
to convert 12-bit output from the CCD’s analog-to-digital convert-
ers to 8-bit values commonly used to store images. As with film,
the most significant nonlinearity in the response curve is at its sat-
uration point, where any pixel with a radiance above a certain level
is mapped to the same maximum image value.
Why is this any problem at all? The most obvious difficulty,
as any amateur or professional photographer knows, is that of lim-
ited dynamic range—one has to choose the range of radiance values
that are of interest and determine the exposure time suitably. Sunlit
scenes, and scenes with shiny materials and artificial light sources,
often have extreme differences in radiance values that are impossi-
ble to capture without either under-exposing or saturating the film.
To cover the full dynamic range in such a scene, one can take a series
of photographs with different exposures. This then poses a prob-
lem: how can we combine these separate images into a composite
radiance map? Here the fact that the mapping from scene radiance
to pixel values is unknown and nonlinear begins to haunt us. The
purpose of this paper is to present a simple technique for recover-
ing this response function, up to a scale factor, using nothing more
than a set of photographs taken with varying, known exposure du-
rations. With this mapping, we then use the pixel values from all
available photographs to construct an accurate map of the radiance
in the scene, up to a factor of scale. This radiance map will cover
剩余9页未读，继续阅读
资源评论
leesyne12015-10-28这个我下载过很好的文章 可是为什么要下载积分- gg4720314942014-09-11是完整的文档
