没有合适的资源?快使用搜索试试~ 我知道了~
FEDformer.pdf
需积分: 0 0 下载量 19 浏览量
2024-04-18
19:46:24
上传
评论
收藏 540KB PDF 举报
温馨提示

试读
19页
FEDformer.pdf
资源推荐
资源详情
资源评论

arXiv:2201.12740v3 [cs.LG] 16 Jun 2022
FEDformer: Frequency Enhanced Decomposed Transformer for Long-term
Series Forecasting
Tian Zhou
* 1
Ziqing Ma
* 1
Qingsong Wen
1
Xue Wang
1
Liang Sun
1
Rong Jin
1
Abstract
Although Transformer-based methods have sig-
nificantly improved state-of-the-art results for
long-ter m series forecasting, they are not only
computationally expensive but more importa ntly,
are una ble to capture the global view of time
series (e.g. overall trend). To address these
problems, we propose to combine Transfor mer
with the seasonal-trend decomposition method,
in which the decomposition method captu res the
global profile of time series while Transformers
capture more detailed structures. To further en-
hance the perform ance of Transformer for long-
term prediction, we exploit the fact that most
time series tend to have a sparse representation
in well-known basis such as Fourier tra nsform,
and develop a frequency enhance d Transformer.
Besides being more effective, the pro posed
method, termed as Frequency Enhanced Decom-
posed Transformer (FEDformer), is more effi-
cient than standard Transformer with a line ar
complexity to the sequenc e length. Our empiri-
cal studies with six benchmark d a ta sets show that
compare d with state-of-the-art methods, FED-
former can reduce prediction error by 14.8% and
22.6% f or multivariate an d univariate time se-
ries, respectively. Code is publicly available at
https://github.com/MAZiqing /FED former.
1. Introduction
Long- term time series forecasting is a long- standing chal-
lenge in various applications (e.g., energy, weather, traf-
fic, economics). Despite the impressive results achieved
by RNN-typ e methods (Rangapuram et al., 2018; Flunkert
et al.
, 2017), they often suffer from the problem of gradi-
*
Equal contribution
1
Machine Intelligence Technology, Al-
ibaba Group.. Correspondence to: Tian Zhou <tian.zt@alibaba-
inc.com>, Rong Jin <jinrong.jr@alibaba-inc.com>.
Proceedings of the 39
th
International Conference on Machine
Learning, Baltimore, Maryland, USA, PMLR 162, 2022. Copy-
right 2022 by the author(s).
ent vanishing or explod ing (
Pascanu et al., 2013), signifi-
cantly limiting their performance. Following the recent suc-
cess in NLP and CV community (
Vaswani et al., 2017; De-
vlin et al., 2 019; Dosovitskiy et al., 2021; Rao et al., 2021),
Transformer (Vaswani et al., 201 7) has been introduced to
capture long-term dependencies in time series for ecasting
and shows p romising results (
Zhou et al., 2021; Wu et al.,
2021). Sin ce high computational complexity and memory
requirement make it difficult for Transformer to be applied
to long sequence modeling, numero us studies are devoted
to reduce the computational cost of Transformer (
Li et al.,
2019; Kitaev et a l., 2020; Zh ou et al., 2021; Wang et al.,
2020; Xiong et al., 2021; Ma et al., 2021). A through
overview of this line of works can be found in Appendix
A.
Despite the progr e ss mad e by Transformer-based meth-
ods for time series forecasting, they tend to fail in cap-
turing the overall characteristics/distribution of time se-
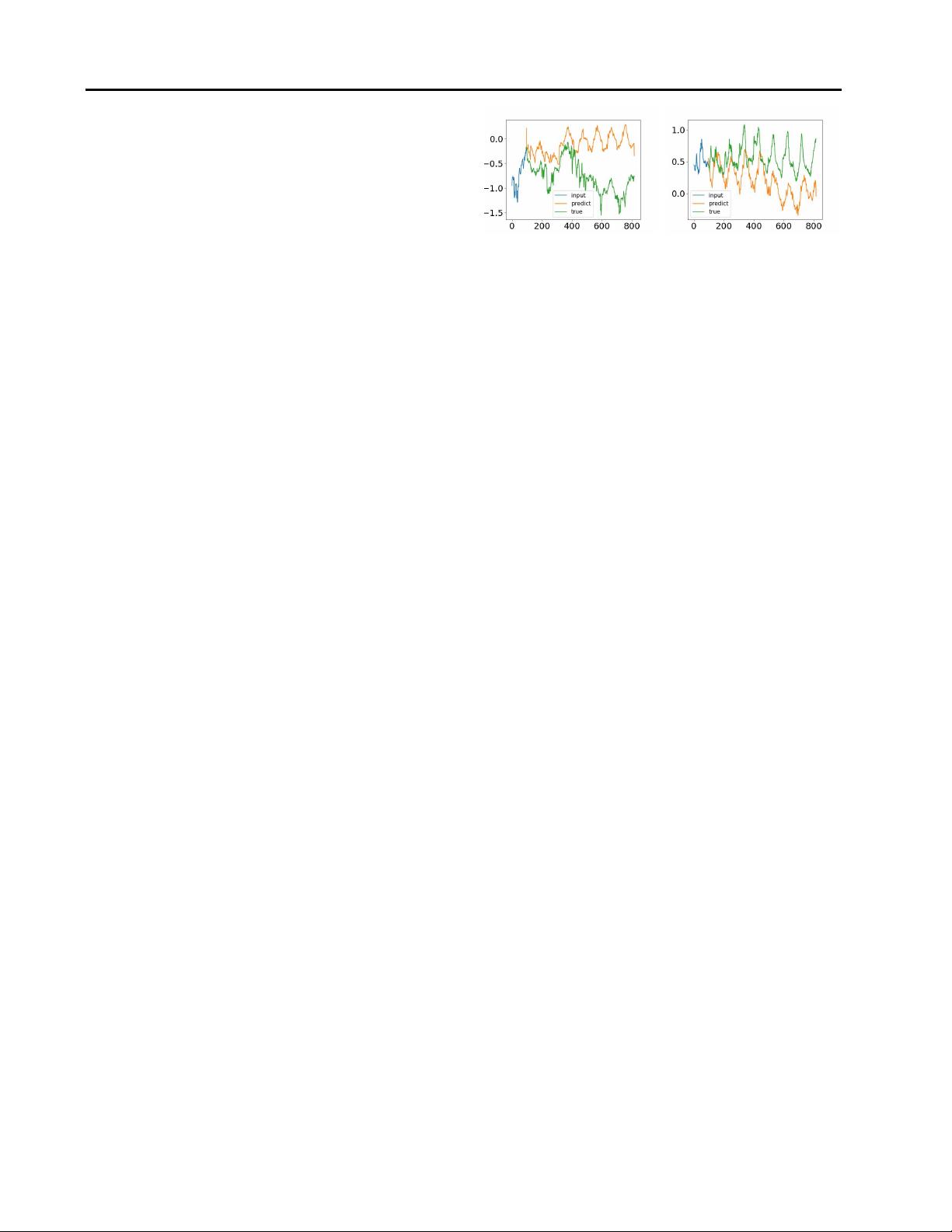
ries in some cases. In Figure
1, we compare the time
series of ground truth with that predicted by the vanilla
Transformer me thod (
Vaswani et al., 2017) in a re al-world
ETTm1 dataset (Zhou et al., 2021). It is clear that the pre-
dicted time series shared a different distribution from that
of ground truth. The discrepancy between ground truth
and p rediction could be explained by the point-wise atten-
tion an d prediction in Transformer. Since pre diction for
each timestep is made individually and independently, it
is likely that the model fails to maintain the global prop-
erty and statistics of time series as a whole. To address
this problem, we exploit two ideas in this work. The first
idea is to incorporate a seasonal- trend decomposition ap-
proach (Cleveland et al., 1990; Wen et al., 2019), which is
widely used in time series analysis, into the Transformer-
based method. Although this idea has been exploited be-
fore (
Oreshkin et al., 2019; Wu et al., 20 21), we present a
special design of network that is effective in bringing the
distribution of prediction close to that of ground truth, ac-
cording to Kologrov-Smirnov distribution test. Our second
idea is to combine Fourier analysis with the Transfo rmer-
based method. Instead o f applying Tr a nsformer to the time
domain, we ap ply it to the frequency domain which helps
Transformer b e tter capture global p roperties of time series.
Combining both ideas, we propose a Frequency Enhanced
Submission and Formatting Instructions for ICML 2022
Decomposition Transformer, or, FEDformer for short, for
long-ter m time ser ie s forecasting.
One critical que stion with FEDformer is which su bset of
frequency components should be used by Fourier analysis
to represent time series. A common wisdom is to keep low-
frequency components and throw away the high-frequency
ones. This may not be appropriate for time series forecast-
ing as some of tre nd changes in time ser ies ar e related to im-
portant events, and this piece of information could be lost
if we simp ly remove all high-frequency components. We
address this problem by effectively exploiting the fact that
time ser ie s tend to have (unknown) sparse represen tations
on a basis like Fourier basis. According to our theoretical
analysis, a randomly selected subset of fre quency compo-
nents, including both low and high ones, will give a better
representation for time series, which is further verified by
extensive empirical studies. Besides b eing more effective
for long term forecasting, combining Transformer with fre-
quency analysis allows us to reduce the computational cost
of Transformer fr om quadratic to linear complexity. We
note that this is different from previous efforts on speeding
up Transformer, which often leads to a performanc e dr op.
In short, we summarize the key contributions of this work
as follows:
1. We propose a frequency enhanced decompo sed Trans-
former architecture with mixture of experts for
seasonal-trend decomposition in order to better cap-
ture global properties of time series.
2. We propo se Fourier enhanced blocks and Wavelet
enhan c ed blocks in the Transformer structure that
allows us to capture important stru ctures in time
series through frequency do main mapping. They
serve as substitutions for both self-attention and cross-
attention blocks.
3. By randomly selecting a fixed number of Fourier com-
ponen ts, the proposed model achieves linear computa-
tional complexity and memory cost. The effectiveness
of this selection method is verified both theoretically
and empirically.
4. We conduct extensive expe riments over 6 benchmark
datasets across multiple domains ( energy, traffic, ec o-
nomics, weather and disease). Our empirical stud-
ies show tha t the proposed mode l improves the per-
formance of state-of-the-art meth ods by 14.8% and
22.6% for multivariate and un ivariate forecasting, re-
spectively.
Figure 1.
Different distribution between ground truth and fore-
casting output from vanilla Transformer in a real-world ETTm1
dataset. L eft: frequency mode and trend shift. Right: tr end shift.
2. Compact Representation of Time Series in
Frequency Domain
It is well-known th at time series data can be modeled from
the time domain and frequency domain. One key contribu-
tion o f our work which separates from other long-term fore-
casting algorithms is the frequency-domain operation with
a neural network. As Fourier analysis is a c ommon tool
to dive into the fr e quency domain, while how to appropri-
ately r e present the information in time series using Fourier
analysis is critical. Simply keeping all the frequency com-
ponen ts may re sult in inferior representations since many
high-f requency changes in time series are due to noisy in-
puts. On the other hand, only keeping the low-frequency
components may also be inappr opriate for series forecast-
ing as some trend changes in time series re present impor-
tant events. Instead, keeping a compact representation of
time ser ie s using a small number of selected Fourier com-
ponen ts will lead to efficient compu tation of transformer,
which is crucial for modelling long sequences. We pro-
pose to represen t time series by randomly selecting a con-
stant number o f Fourier components, including both high-
frequency and low-frequency. Below, an analysis that justi-
fies the random selection is presented theoretically. Empir-
ical verification can be found in the experimental session.
Consider we have m time series, denoted as
X
1
(t), . . . , X
m
(t). By applying Fourier transform
to each time ser ies, we turn each X
i
(t) into a vec-
tor a
i
= (a
i,1
, . . . , a
i,d
)
⊤
∈ R
d
. By putting all
the Fourier tra nsform vectors into a matrix, we have
A = (a
1
, a
2
, . . . , a
m
)
⊤
∈ R
m×d
, with each row cor-
respond ing to a different time series and each column
correspo nding to a d ifferent Fourier component. Although
using all the Fourier components allows us to be st preserve
the history information in the time series, it may potentially
lead to overfitting of the history da ta an d con sequentially
a poor prediction of future signals. Hence, we need to
select a subset of Fourier comp onents, that on the one hand
should be small enough to avoid the overfitting problem
and on the oth e r hand, should be able to preserve m ost
of the histor y information. Here, we pr opose to select
s comp onents from the d Fourier components (s < d)
Submission and Formatting Instructions for ICML 2022
Feed
Forward
Frequency
Enhanced
Block
MOE
Decomp
MOE
Decomp
FEDformer Encoder
Frequency
Enhanced
Attention
Frequency
Enhanced
Block
MOE
Decomp
MOE
Decomp
FEDformer Decoder
+ +
N
+ +
+
Feed
Forward
MOE
Decomp
+
Q
+
+ +
Output
M
K
V
Encoder
Input
Seasoal
Init
Trend Init
T
l,2
de
T
l,1
de
T
l,3
de
S
l,2
de
S
l,1
de
S
l,1
en
S
l,2
en
(or X
l
en
)
X
0
en
∈ R
I×D
X
0
de
∈ R
(I/2+O)×D
T
0
de
∈ R
(I/2+O)×D
X
l−1
en
T
l−1
de
X
l−1
de
T
l
de
S
l,3
de
(or X
l
de
)
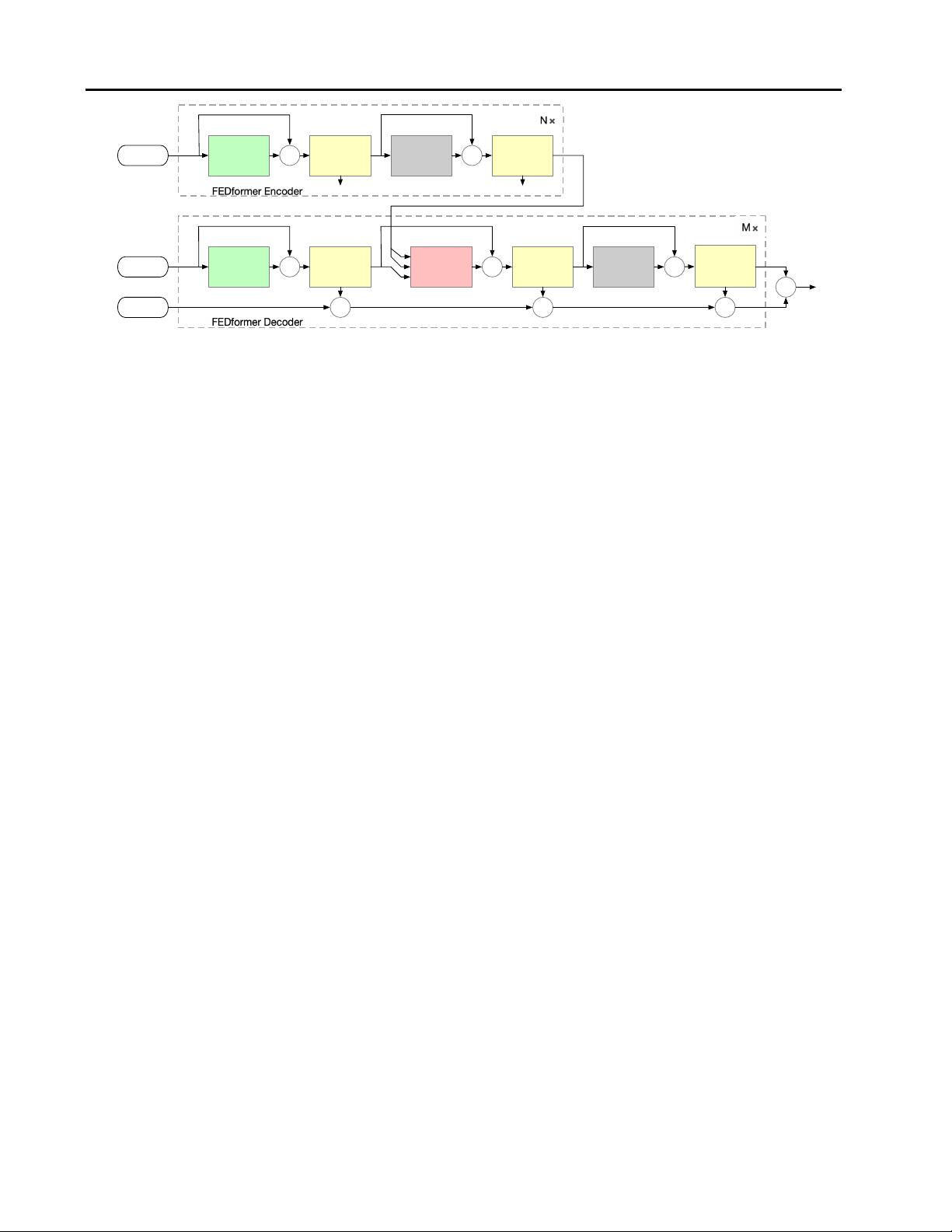
Figure 2.
FEDformer Structure. The FEDformer consists of N encoders and M decoders. The Frequency Enhanced Block (FEB, green
blocks) and Frequency Enhanced Attention (FEA, red blocks) are used to perform representation learning in frequency domain. E ither
FEB or FEA has two subversions (FEB-f & FEB-w or FEA-f & FEA-w), where ‘-f’ means using Fourier basis and ‘-w’ means using
Wavelet basis. The Mixture Of Expert Decomposition Blocks (MOEDecomp,
yellow blocks) are used to extract seasonal-trend patterns
from the input data.
unifor mly at random. More specifically, we denote by
i
1
< i
2
< . . . < i
s
the randomly selected components.
We construct matrix S ∈ {0, 1}
s×d
, with S
i,k
= 1 if
i = i
k
and S
i,k
= 0 otherwise. Then, our representation
of multivaria te time series becomes A
′
= AS
⊤
∈ R
m×s
.
Below, we will show that, although the Fourier basis are
randomly selected, under a mild condition, A
′
is able to
preserve most of the information from A.
In orde r to measure how well A
′
is able to preserve informa-
tion from A, we project each column vector of A into the
subspace spanned by the column vectors in A
′
. We denote
by P
A
′
(A) the resulting matrix after the projection, where
P
A
′
(·) rep resents the projection operator. If A
′
preserves
a large portion of information from A, we would expect a
small error between A and P
A
′
(A), i.e. |A −P
A
′
(A)|. Let
A
k
represent the approximatio n of A by its first k largest
single value de composition. The the orem below shows that
|A−P
A
′
(A)|is clo se to |A−A
k
|if the number of randomly
sampled Fourier components s is on the order of k
2
.
Theorem 1. Assume that µ(A), the coherence measure of
matrix A, is Ω(k/n). Then, with a high probability, we
have
|A − P
A
′
(A)| ≤ (1 + ǫ)|A − A
k
|
if s = O(k
2
/ǫ
2
).
The detailed analysis can be foun d in Appendix
C.
For real-world multivariate times series, the c orresponding
matrix A from Fourier transform often exhibit low rank
property, since those univaraite variables in multivariate
times series depend no t only on its past values but a lso
has dependency on each other, as well as share similar fre-
quency components. Therefore, as indic ated by the The-
orem
1, ran domly selecting a subset of Fourie r compo-
nents allows us to appropriate ly represent th e information
in Fourier matrix A.
Similarly, wavelet orthogonal polynomials, suc h as Legen-
dre Polynomials, obey restricted iso metry property (RIP)
and can be used for c a pture infor mation in time series as
well. Compared to Fourier b asis, wavelet based re presenta-
tion is more effective in captur ing local structu res in time
series and thus can be more effective for some forecasting
tasks. We defer the discussion of wavelet based representa-
tion in Appendix
B. In the next section, we will present the
design of frequency enhanced d e composed Transformer ar-
chitecture that incorporate the Fourier transform into trans-
former.
3. Model Structure
In this section, we will introdu ce (1) the overall structure
of FEDformer, as shown in Fig ure
2, (2) two subversion
structures for signal process: one uses Fourier basis and
the other u ses Wavelet basis, (3) the mixture of experts
mechanism for seasonal-trend decomposition, and (4) the
complexity analysis of the proposed model.
3.1. FEDformer Framework
Preliminary Long-term time series forecasting is a se-
quence to sequence problem. We denote the input length
as I and output length as O. We denote D as the hidden
states of the series. The input of th e encoder is a I × D
matrix and the decoder has (I/2 + O) × D in put.
FEDformer Structure Inspired by the seasonal-tr end de-
composition and distribution ana lysis as discussed in Sec-
tion
1, we renovate Transformer as a deep decomposition
architecture as shown in Figure 2, including Frequency
Enhance d Block (FEB), Frequency Enhanced Attention

Submission and Formatting Instructions for ICML 2022
(FEA) conn ecting encoder and decoder, and the Mixture
Of Experts Decomposition block (MOEDe c omp). The de-
tailed description of FEB, FEA, a nd MOEDecomp blocks
will be given in the following Section
3.2, 3.3, and 3.4 re-
spectively.
The encoder adopts a multilayer structure as: X
l
en
=
Encoder(X
l−1
en
), where l ∈ {1, ··· , N} denotes the out-
put of l-th encoder layer and X
0
en
∈ R
I×D
is the embed ded
historical series. The Enc oder(·) is formalized as
S
l,1
en
,
−
= MOEDecomp(FEB
X
l−1
en
+ X
l−1
en
),
S
l,2
en
,
−
= MOEDecomp(FeedForward
S
l,1
en
+ S
l,1
en
),
X
l
en
= S
l,2
en
,
(1)
where S
l,i
en
, i ∈ {1, 2} represents the seasonal compo-
nent a fter the i-th decomposition block in th e l-th layer r e-
spectively. For FEB module, it has two d ifferent versions
(FEB-f & FEB-w) which are implemented through Discrete
Fourier transform (DFT) and Discrete Wavelet transform
(DWT) mechanism respec tively and can seamlessly re place
the self- attention bloc k.
The decoder also a dopts a multilayer structure as:
X
l
de
, T
l
de
= D e coder(X
l−1
de
, T
l−1
de
), where l ∈ {1, ··· , M}
denotes the output of l-th decoder lay er. The Decoder(·) is
formalized as
S
l,1
de
, T
l,1
de
= MOEDecomp
FEB
X
l−1
de
+ X
l−1
de
,
S
l,2
de
, T
l,2
de
= MOEDecomp
FEA
S
l,1
de
, X
N
en
+ S
l,1
de
,
S
l,3
de
, T
l,3
de
= MOEDecomp
FeedForward
S
l,2
de
+ S
l,2
de
,
X
l
de
= S
l,3
de
,
T
l
de
= T
l−1
de
+ W
l,1
·T
l,1
de
+ W
l,2
·T
l,2
de
+ W
l,3
·T
l,3
de
,
(2)
where S
l,i
de
, T
l,i
de
, i ∈ {1, 2, 3 } represent the seaso nal and
trend component after the i-th decomposition block in the l-
th layer respectively. W
l,i
, i ∈ {1, 2, 3} represents the pro-
jector for the i-th extracted trend T
l,i
de
. Similar to FEB, FEA
has two different versions (FEA-f & FEA-w) which are im-
plemented through DFT and DWT projectio n respectively
with attention design, and can replace the cross-attention
block. The detailed description of FEA(·) will be given in
the following Section
3.3.
The final prediction is the sum of the two r e fined decom-
posed components as W
S
· X
M
de
+ T
M
de
, where W
S
is to
project the d e ep transformed seasonal component X
M
de
to
the target dimensio n.
3.2. Fourier Enhanced Structure
Discrete Fourier Transform (DFT) The proposed
Fourier Enhanced Structures u se discrete Fourier transfor m
(DFT). Le t F denotes the Fourier transform and F
−1
de-
F
F
−1
q ∈ R
L×D
Sampling
×
Q ∈ C
N ×D
C
M ×D
˜
Q ∈
R ∈
˜
Y ∈
C
M ×D
padding
Y ∈ C
N ×D
y ∈ R
L
de
×D
C
M ×D×D
X
l−1
en/de
MLP
Figure 3.
Frequency Enhanced Block with Fourier transform
(FEB-f) structure.
×
MLP
v
F + Sampling
MLP
MLP
˜
Q
˜
K
˜
V
F + Sampling
F + Sampling
σ(·)
×
Padding + F
−1
y ∈ R
L
de
×D
q ∈ R
L
de
×D
k
˜
Q
˜
K
⊤
X
l
en
S
l,1
de
Figure 4.
Frequency Enhanced Attention with Fourier transform
(FEA-f) structure, σ(·) is the activation function.
notes the inverse Fourier transform. Given a sequence of
real numbers x
n
in time domain, where n = 1, 2...N. DFT
is defined as X
l
=
P
N−1
n=0
x
n
e
−iωln
, where i is the im a g-
inary unit and X
l
, l = 1, 2...L is a sequence o f complex
numbers in the frequency domain. Similarly, the inverse
DFT is defined as x
n
=
P
L−1
l=0
X
l
e
iωln
. The complex-
ity of DFT is O(N
2
). With fast Fourier transform (FFT),
the computation complexity can be reduced to O(N log N).
Here a random subset of the Fourier basis is used and
the scale of the subset is b ounded by a scalar. When we
choose the mode index b efore DFT and reverse DFT oper-
ations, the computation complexity can be further red uced
to O(N).
Frequency Enhanced Block with Fourier Transform
(FEB-f) The FE B-f is used in both encoder and decoder
as shown in Figure
2. The input (x ∈ R
N×D
) of the
FEB-f block is first linearly projected with w ∈ R
D×D
, so
q = x·w. Then q is converted f rom the time dom ain to the
frequency domain. The Fourier transform of q is denoted
as Q ∈ C
N×D
. In frequency domain , only the randomly
selected M modes are kept so we use a select operator as
˜
Q = Select(Q) = Select(F(q)), (3)
where
˜
Q ∈ C
M×D
and M << N. Then, the FEB-f is
defined as
FEB-f(q) = F
−1
(Padding(
˜
Q ⊙ R)), (4)
where R ∈ C
D×D×M
is a parameterized kernel in itialized
randomly. Let Y = Q ⊙ C, with Y ∈ C
M×D
. The pro-
duction operator ⊙ is defined as: Y
m,d
o
=
P
D
d
i
=0
Q
m,d
i
·
R
d
i
,d
o
,m
, where d
i
= 1, 2...D is the input channel and
d
o
= 1, 2...D is the output chan nel. The result of Q ⊙ R
is then z e ro-padded to C
N×D
before performing inverse
Fourier transform bac k to the time domain. T he structure
is shown in Figure
3.
剩余18页未读,继续阅读
资源评论

Chase~711
- 粉丝: 0
- 资源: 1
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- 三维装箱问题(Three-Dimensional Bin Packing Problem,3D-BPP)是一个经典的组合优化问题
- 以下是一些关于Linux线程同步的基本概念和方法.txt
- 以下是一个简化的示例,它使用pygame库来模拟烟花动画的框架.txt
- Linux线程同步机制深度解析与实用指南.zip
- PTA题库C语言解题策略与实战.rar
- SVPWM控制技术的simulink建模与仿真【包括simulink模型,参考文献,操作步骤】
- AI高清修复图片画质易语言易语言源码易语言填表
- 映射窗口.ec易语言易语言模块CPU占用0%游戏监控窗口监控
- 易语言 361窗口模块高效、便捷、自封装、自用
- 易语言 窗口排列 模块 ,简单、高效、体积小
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功