设有一有向图为g(vdoc (2).pdf
2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
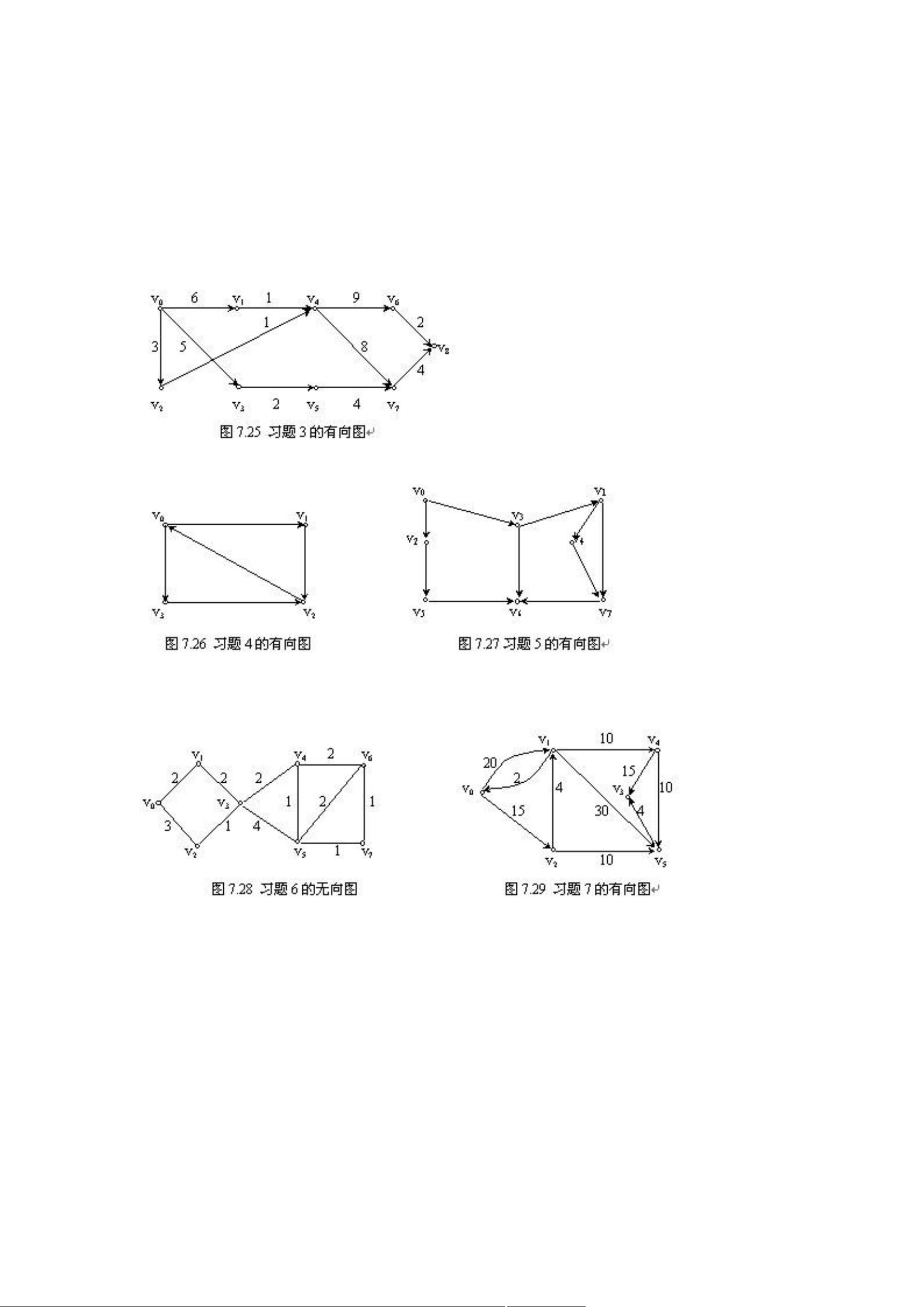
在IT领域,图是一种重要的数据结构,用于表示对象之间的关系。本题主要涉及有向图、无向图、邻接矩阵、邻接表、强连通分量、最短路径算法(Dijkstra、Floyd)、最小生成树算法(Prim、Kruskal)、拓扑排序、完全二叉树和AOE网等概念。 1. 有向图G=(V,E)的定义:V是顶点集合,E是边集合。给定的有向图V={v0, v1, v2, v3},E={<v1, v0>, <v2, v1>,<v3, v2>, <v3, v1>, <v0, v3>},可以直观地画出这个图,其中箭头表示边的方向。 2. 无向图的邻接矩阵表示:这是一个二维数组,行和列对应图中的顶点,如果两个顶点之间有边,则对应位置的值为1,没有边则为0。用邻接矩阵可以快速判断任意两个顶点间是否有边,以及计算顶点的度(入度+出度)。 3. 带权有向图的邻接矩阵表示和邻接表表示:邻接矩阵中非对角线元素表示边的权重,邻接表则是每个顶点对应的边列表,可以节省空间。 4. 强连通分量:一个有向图是强连通的,如果图中任意两个顶点都互相可达。图7.26需要分析是否存在这样的路径。 5. 深度优先搜索(DFS)和广度优先搜索(BFS):DFS从给定顶点出发,沿着边尽可能深地探索,而BFS则优先探索距离起点近的顶点。对于图7.27,从v0出发可以画出这两种生成树。 6. Prim和Kruskal算法:Prim算法从一个顶点开始逐步添加边,形成最小生成树,而Kruskal算法按边的权重从小到大选择,避免形成环路。两者用于构建无环加权图的最小生成树。 7. Dijkstra算法:求单源最短路径,按路径长度从小到大扩展,记录每次更新后的Dist数组和路径信息。 8. Floyd算法:计算所有顶点间的最短路径,通过动态规划更新最短路径矩阵Ai和最短路径中间节点nextvexi。 9. 拓扑排序:有向无环图的顶点排序,使得每条边指向的顶点都出现在其起点之后。图7.31可能存在多种合法的拓扑序列。 10. 无环有向图的关系矩阵:通过调整顶点顺序,可以使得对角线以下元素全为0,因为不存在环,所以从一个顶点无法到达它自己或更低位置的顶点。 11. 完全二叉树的邻接表和邻接矩阵:完全二叉树的邻接矩阵是对称的,邻接表反映了父子节点关系。 12. 深度优先遍历(DFS)和广度优先遍历(BFS)森林:从顶点V1开始,DFS和BFS会产生不同的树结构,因为DFS可能先访问子树的深处,而BFS则按层次遍历。 13. 无向图的邻接表构造:根据输入的顶点对创建邻接表,并从顶点4开始进行DFS和BFS遍历,记录顺序。 14. Dijkstra算法求最短路径:在有向网中,从源点1开始,逐步扩大红点集(已找到最短路径的顶点),直到所有顶点都包含在内。 15. 无前趋顶点优先的拓扑排序:找到没有入边的顶点开始,按顺序输出顶点。 16. AOE网的关键路径:关键活动是那些影响工程完成时间的活动,它们的最早开始时间和最晚开始时间相等。提高关键活动的速度可以提前工程的完成时间。 在实现这些算法时,选择不同的数据结构(如邻接矩阵、邻接表)会影响算法的效率,例如邻接表通常比邻接矩阵更适合处理稀疏图,而邻接矩阵在处理稠密图时更高效。在实际编程中,应根据具体问题选择合适的数据结构。

- 粉丝: 4076
- 资源: 1万+
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功