Journal of Machine Learning Research ? (2008) 1-?? Submitted 4/08; Published ??/08
BNT STRUCTURE LEARNING PACKAGE :
Documentation and Experiments
Olivier C.H. FRANCOIS Francois.Olivier.C.H@gmail.com
Sustainable Urban Environments Research Division, URS building, Room 3n38,
Whiteknights, PO Box 219, Reading, RG6 6AW, UK
http: // ofrancois. tuxfamily. org
Philippe LERAY Philippe.Leray@univ-nantes.fr
Ecole Polytechnique de l’Université de Nantes,
Laboratoire d’Informatique de Nantes Atlantique,
Rue Christian Pauc, BP 50609, 44306 Nantes Cedex 3
http: // www. polytech. univ-nantes. fr/ COD/ ?Pages_ personnelles: Philippe_ Leray
Editor: ?? Leslie Pack Kaelbling ??
Abstract
Bayesian networks are a formalism for probabilistic reasoning that have grown in-
creasingly popular for tasks such as classification in data-mining. In some situations,
the structure of the Bayesian network can be given by an expert. If not, retrieving
it automatically from a database of cases is a NP-hard problem; notably because of
the complexity of the search space. In the last decade, numerous methods have been
introduced to learn the network’s structure automatically, by simplifying the search
space or by using an heuristic in the search space. Most methods deal with completely
observed data, but some can deal with incomplete data. The Bayes Net Toolbox for
Matlab, introduced by Murphy (2004), offers functions for both using and learning
Bayesian Networks. But this toolbox is not ’state of the art’ as regards structural
learning methods. This is why we propose the SLP package.
Keywords: Bayesian Networks, Structure Learning, Classification
1. Introduction
Bayesian networks are probabilistic graphical models introduced by Kim and Pearl
(1987), Lauritzen and Spiegelhalter (1988), Jensen (1996), Jordan (1998).
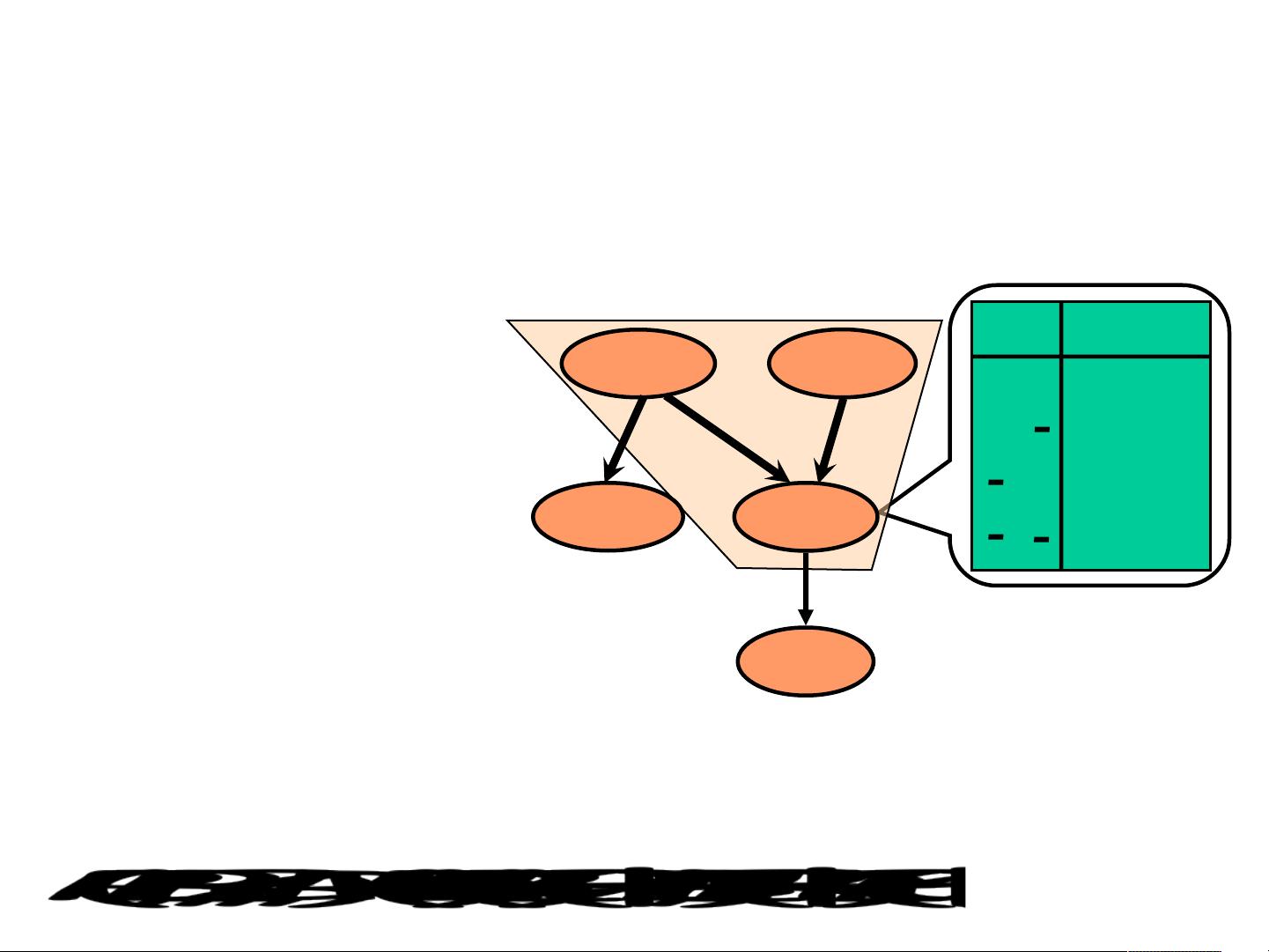
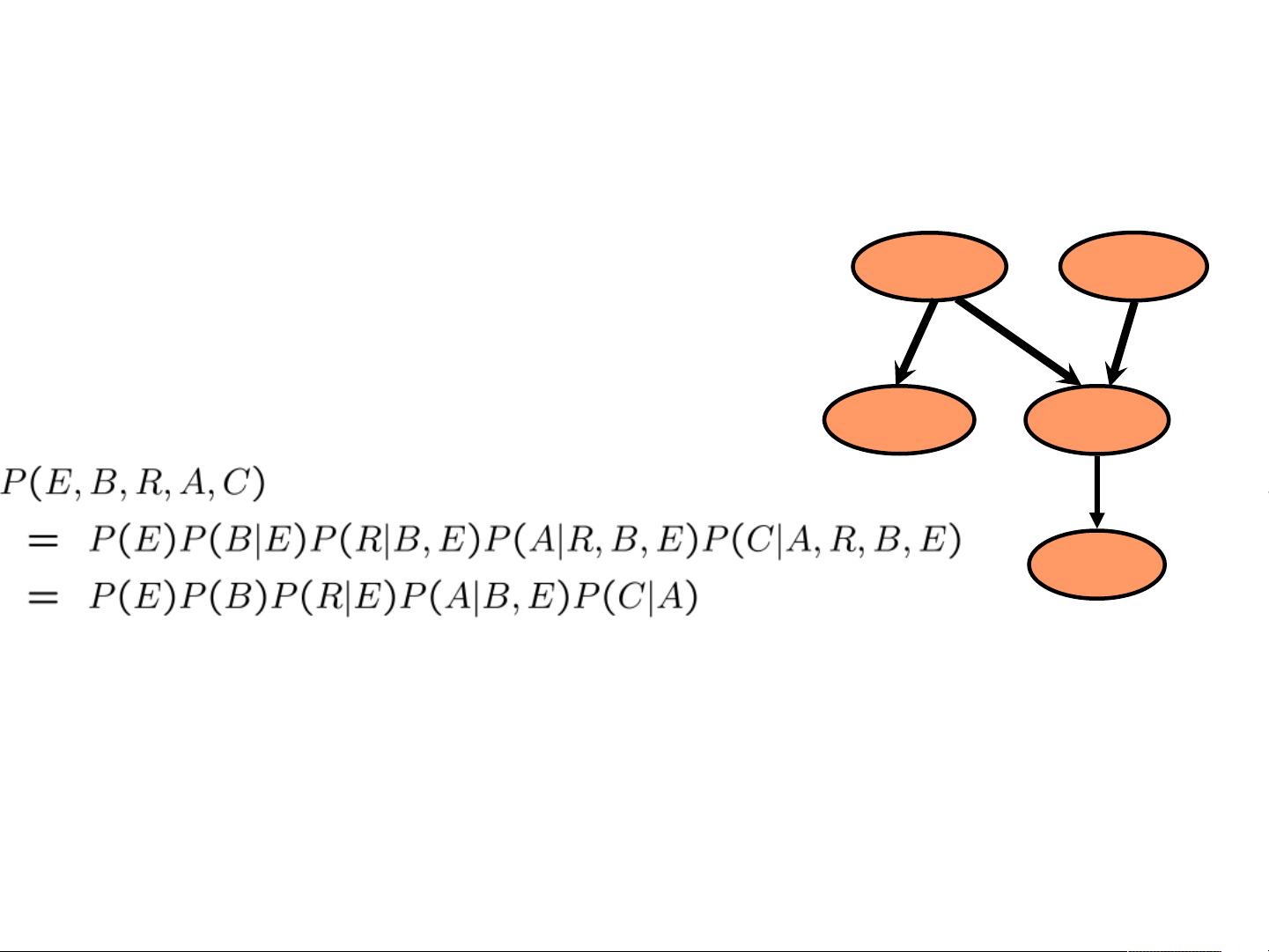
Definition 1. B = (G,θ) is a discrete bayesian network (or belief network) if G = (X, E)
is a directed acyclic graph (DAG) where the set of nodes represents a set of random
variables X = {X
1
, · · · , X
n
}, and if θ
i
= [P(X
i
/X
Pa(X
i
)
) ] is the matrix containing the
conditional probability of node i given the state of its parents Pa(X
i
).
A Bayesian network B represents a probability distribution over X which admits the
following joint distribution decomposition:
P(X
1
, X
2
, · · · , X
n
) =
n
∏
i=1
P(X
i
/X
Pa(X
i
)
) (1)
This decomposition allows the use of some powerful inference algorithms for which
Bayesian networks became simple modeling and reasoning tools when the situation is
c
2008 Olivier François and Philippe Leray.