某学长讲课ppt（前缀和与差分，二维前缀和与差分）

一、内容概述 本资源是一份详尽的关于前缀和与差分的PPT制作素材，旨在帮助使用者通过视觉化的方式，全面而深入地理解这两个在计算机科学中至关重要的概念。PPT内容从基本概念讲起，逐步深入到一维和二维前缀和与差分的计算，以及实际应用示例，旨在为读者提供一套完整的学习体系。 二、主要部分 封面与目录：包含简洁明了的标题和目录结构，为观众提供整体内容预览。 前缀和基本概念：详细解释前缀和的定义、性质及其在计算连续子数组和中的作用，通过文字和图表相结合的方式，帮助观众建立基本概念框架。 一维前缀和与差分的计算：通过具体案例和计算步骤，详细展示如何构造一维前缀和数组，以及如何根据前缀和数组计算差分数组，同时强调它们在算法优化中的应用。 二维前缀和与差分的计算：在一维的基础上，进一步讲解二维前缀和与差分的计算方法，结合图表和实例，展现其在图像处理、矩阵计算等领域的应用价值。 应用示例：通过算法竞赛、数据处理等实际场景中的应用案例，展示前缀和与差分在实际问题中的应用方法和效果，加深观众的理解和应用能力。 总结与回顾：对整个PPT内容进行总结，强调前缀和与差分的重要性，鼓励大家在实际编程 ### 前缀和与差分算法详解及应用 #### 一、前缀和与差分算法概述 **前缀和**与**差分**是在计算机科学领域内极为重要的两个概念，尤其在算法设计与优化方面有着广泛的应用。这两种算法不仅能够显著提高计算效率，还能简化复杂的数学问题。本文将从基本概念入手，逐步深入到一维和二维前缀和与差分的计算方法，并通过实际应用场景来展示这些算法的强大之处。 #### 二、前缀和算法 **1. 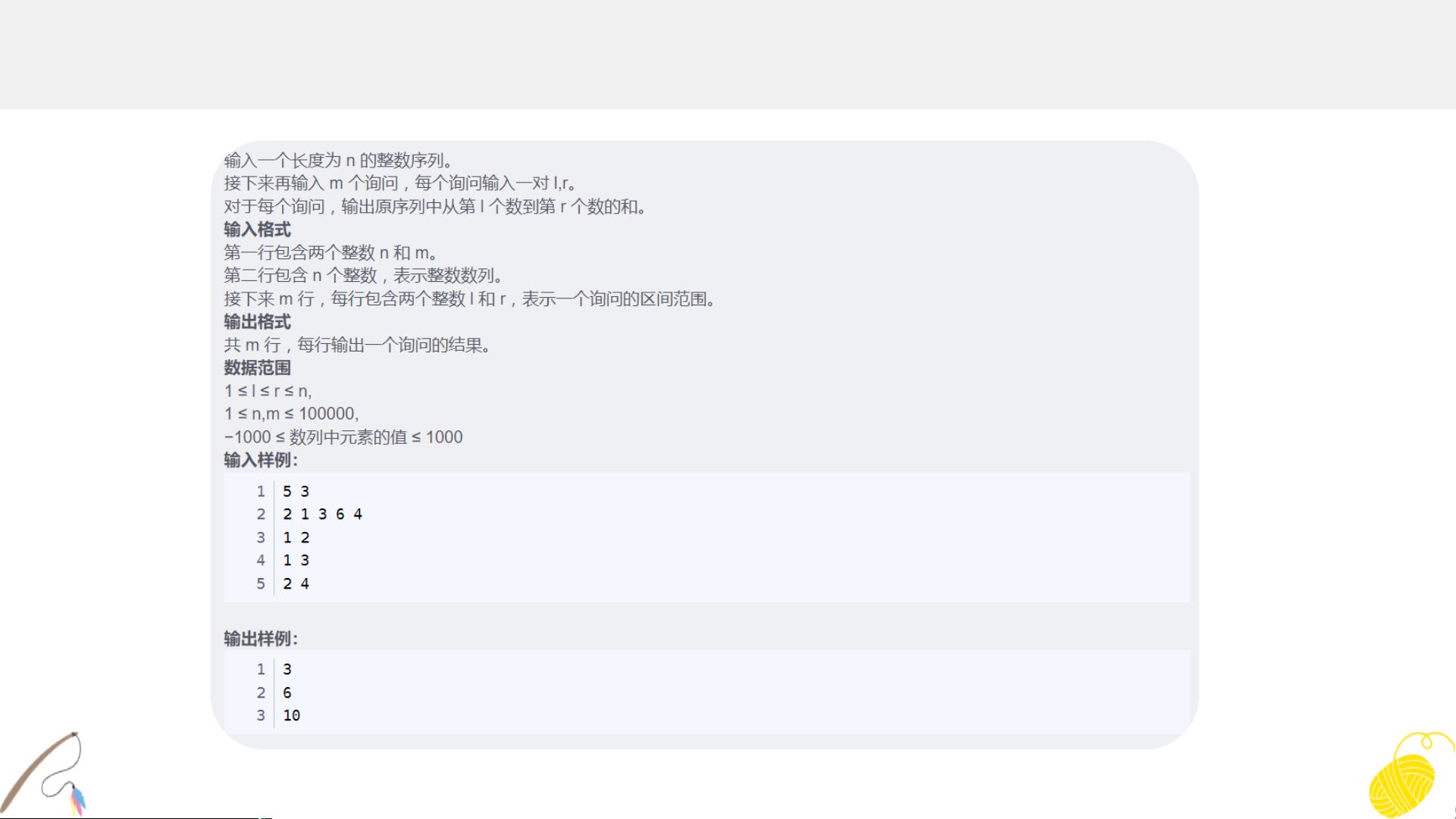定义与基本概念** 前缀和算法主要用于计算数组或序列中从起始位置到当前位置所有元素的累加和。其核心思想是通过预处理创建一个辅助数组，该数组的每个元素代表原数组中对应位置的前缀和。 **2. 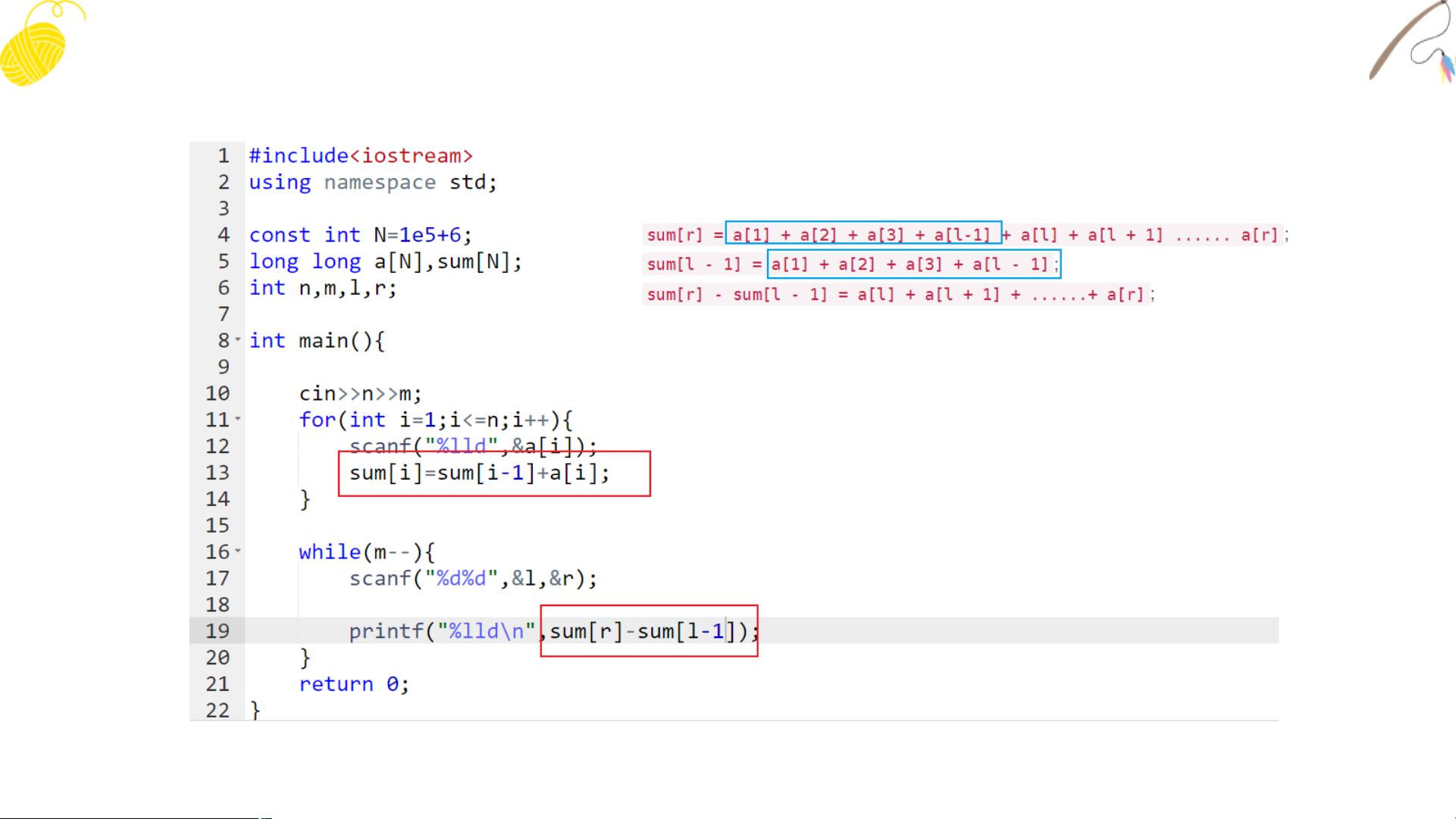实现步骤** - **预处理**：创建与原数组相同大小的辅助数组，用于存储每个位置的前缀和。将辅助数组的第一个元素设置为原数组的第一个元素。从第二个位置开始，计算当前位置的前缀和，即原数组当前位置的元素加上辅助数组中前一个位置的元素。 - **查询前缀和**：完成预处理后，可以通过查询辅助数组中的元素来快速获取原数组任意区间的前缀和。例如，给定区间\[l, r\]，前缀和可通过辅助数组的r位置减去辅助数组的\(l-1\)位置来计算。 **3. 时间复杂度分析** - **预处理**：O(n)，其中n为原数组长度。 - **查询**：O(1)，查询操作无论区间大小如何，时间复杂度始终为常数级别。 #### 三、差分算法 **1. 定义与基本概念** 差分算法则主要用于高效地对数组或序列进行增量更新操作。其核心思想是将原数组中相邻元素之间的差值存储在另一个数组中，这个数组被称为差分数组。 **2. 实现步骤** - **创建差分数组**：创建与原数组相同大小的差分数组，初始值均为0。差分数组的每个位置存储原数组中相邻元素之间的差值。 - **更新操作**：对原数组进行增量更新时，只需对差分数组的特定区间进行修改。例如，若在原数组的区间\[l, r\]上增加一个值val，则需将差分数组的第l个元素增加val，第\(r+1\)个元素减去val。 - **恢复原数组**：通过计算差分数组的前缀和来恢复更新后的原数组。创建一个辅助数组，初始值为0，然后从差分数组的第一个位置开始计算当前位置的前缀和，并将结果存储在辅助数组中。 **3. 时间复杂度分析** - **创建差分数组**：O(n)，其中n为原数组长度。 - **恢复原数组**：O(n)，需要遍历整个差分数组来计算每个位置的前缀和。 #### 四、二维前缀和与差分 在二维空间中，前缀和与差分的概念同样适用，但涉及到的是矩阵而不是一维数组。 **1. 二维前缀和** - **定义**：二维前缀和用于计算矩阵中任意子矩阵元素的累加和。 - **实现步骤**：创建一个与原矩阵相同大小的辅助矩阵，存储每个位置的二维前缀和。通过累加相邻元素来计算当前位置的前缀和。 - **查询**：通过辅助矩阵中的相应元素来快速计算任意子矩阵的累加和。 **2. 二维差分** - **定义**：二维差分用于高效地对矩阵进行增量更新操作。 - **实现步骤**：创建与原矩阵相同大小的差分矩阵，存储每个位置的差值。更新操作涉及对差分矩阵的特定区域进行修改。 - **恢复原矩阵**：通过计算差分矩阵的二维前缀和来恢复更新后的原矩阵。 #### 五、实际应用 前缀和与差分算法在多个领域都有着广泛的应用： - **算法竞赛**：解决与数组和矩阵相关的复杂问题。 - **图像处理**：高效处理图像中的像素数据。 - **数据处理**：加速大数据集的统计分析。 #### 六、总结与回顾 通过以上介绍可以看出，前缀和与差分算法在提高计算效率、简化问题求解过程中扮演着极其重要的角色。无论是针对一维数组还是二维矩阵，这些算法都能够提供强大的支持。理解和掌握这两种算法的核心原理及其应用技巧，对于从事计算机科学相关领域的工作者来说至关重要。希望本文能够帮助读者建立起对前缀和与差分算法的系统性认识，并在未来的学习和工作中灵活运用这些工具解决问题。