基于分数低阶矩的干涉阵列米波雷达稳健测高方法.docx

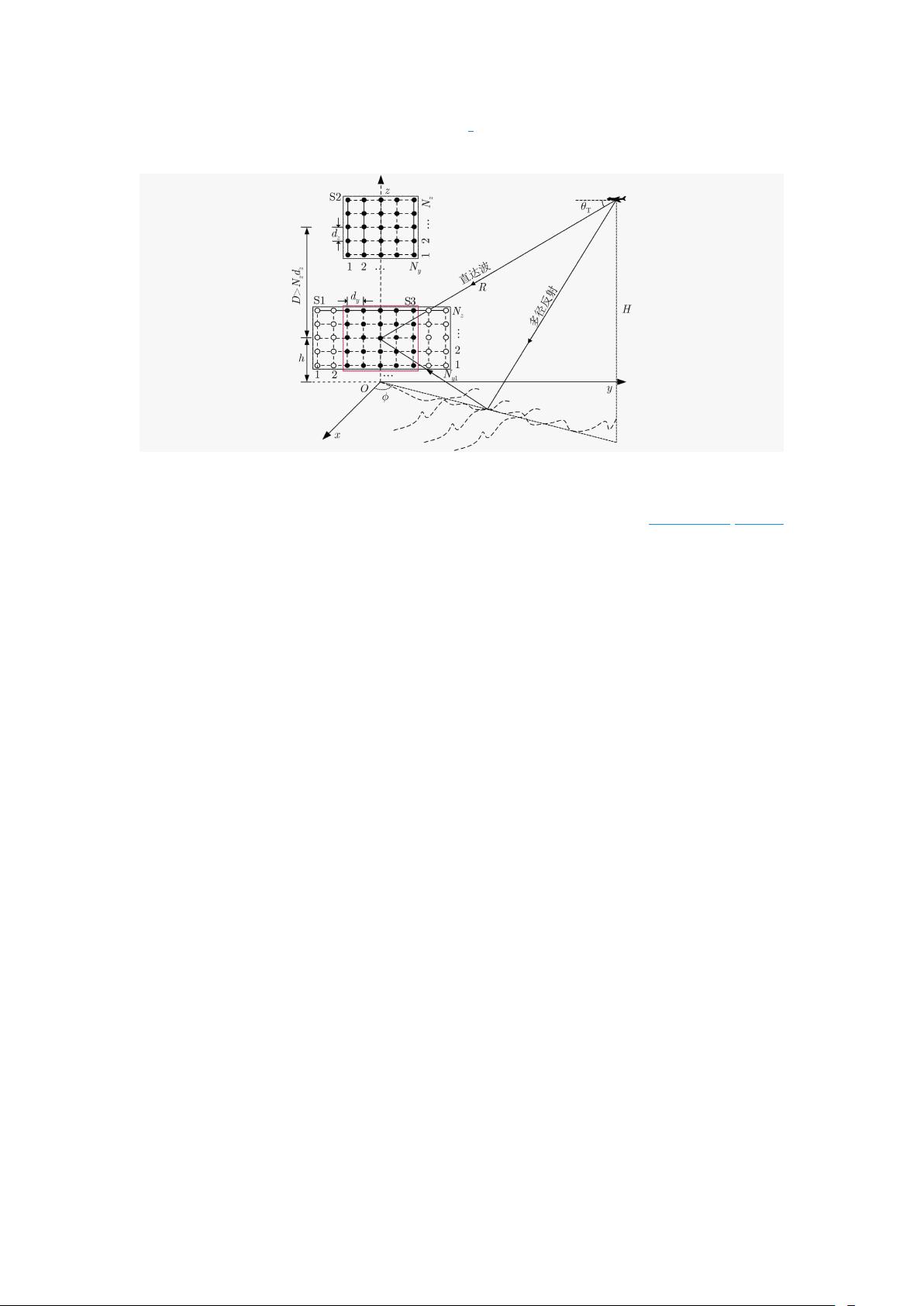
《基于分数低阶矩的干涉阵列米波雷达稳健测高方法》 米波雷达作为反隐身和反辐射导弹防御系统的关键技术，其分辨率和定位精度的提升是研究的重点，尤其是在低角度目标的测高方面。传统的米波雷达在低仰角区域面临两大挑战：一是波束宽度大导致的热杂波干扰，二是复杂多径信号引起的测高误差。为解决这些问题，当前的研究主要集中在超分辨处理技术，如合成导向矢量法和空域滤波法，以及针对复杂多径信号的随机扰动法。然而，这些参数化算法的性能高度依赖于信号模型的准确性，尤其是难以精确建模的非高斯散射分量。 文章提出了一种新的干涉阵列米波雷达测高方法，借鉴InSAR（Interferometric Synthetic Aperture Radar）的干涉技术，通过扩展俯仰孔径和增加基线自由度来提高测高精度和分辨力。具体来说，采用了倒T形干涉阵列，由主收发子阵S1和接收子阵S2组成，两者之间的基线为D，阵元间距分别为dz和dy。S2仅接收目标反射能量，有助于提高目标探测概率。在低角目标测高中，选取S1的子阵S3与S2构成干涉阵列，形成双尺度移不变性和中心对称性的干涉信号。 为了处理非高斯散射分量，文章引入了分数低阶矩理论，通过求解干涉阵列的分数阶协变矩阵，结合2维空间平滑法和双尺度酉ESPRIT算法进行低角测高。这种方法能更稳健地处理非高斯分布的散射信号，提高测高算法的鲁棒性。 此外，文章还提出了干涉阵列的三区基线设计法，将基线范围分为模糊区、高分辨区和非稳定临界区，为实际的干涉阵列设计提供了理论指导。通过仿真结果，验证了该干涉阵列和测高算法的高精度和高分辨性能，同时也证实了三区基线设计法的有效性。 总结来说，本文创新性地将干涉技术和分数低阶矩理论应用于米波雷达测高，克服了传统方法在处理非高斯散射分量和有限自由度的局限，提升了雷达在低角目标测高的准确性和稳定性，对于未来米波雷达技术的发展具有重要的理论和实践意义。