基于星点图椭圆度分布的光学系统装配误差计算方法.docx

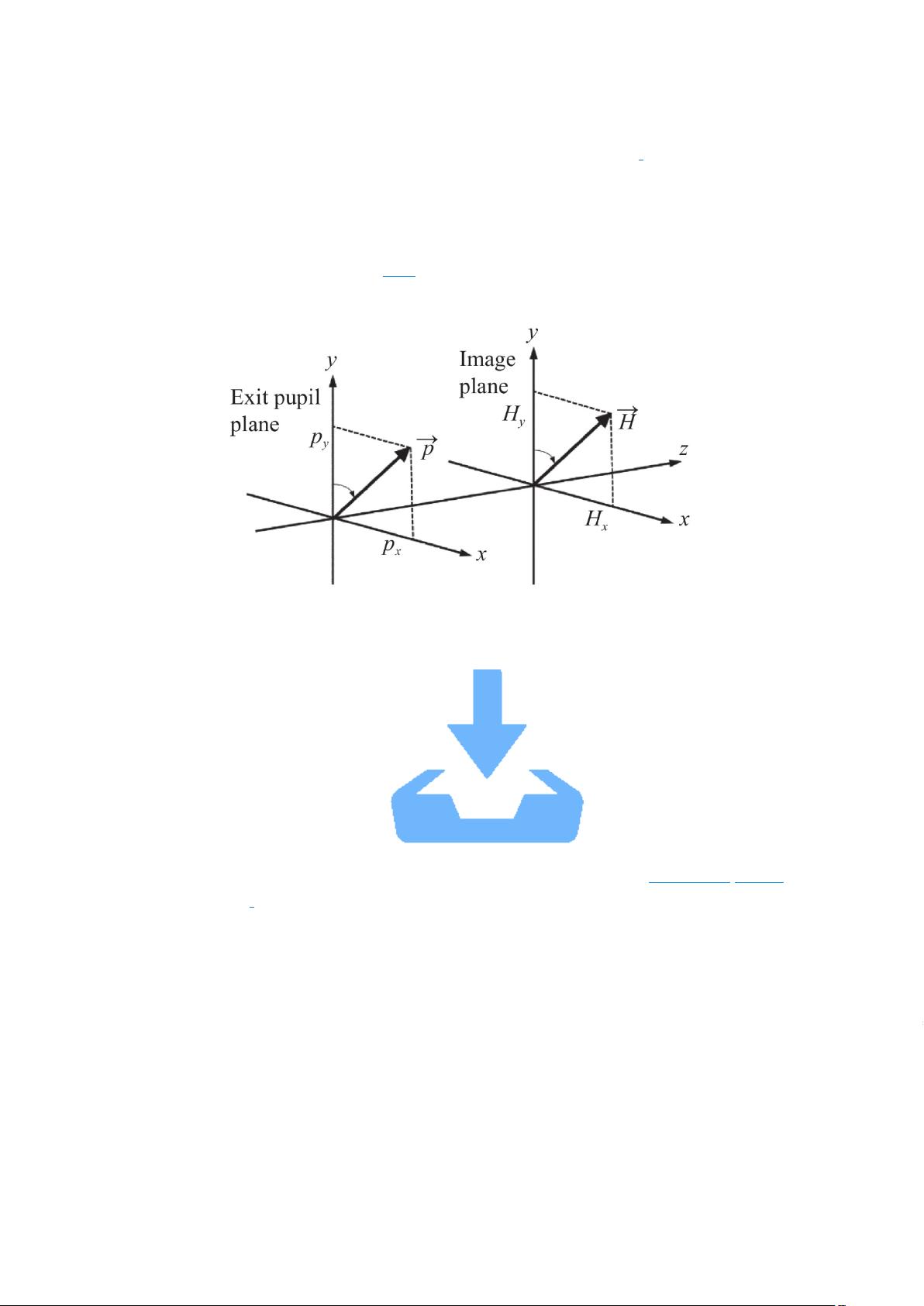
光学系统装配误差的计算是光学工程中的关键环节，它直接影响着光学系统的性能和装调效率。传统的计算方法，如敏感度矩阵法、逆向优化法、神经网络法和基于矢量像差理论的解析计算方法，都依赖于装配误差与波像差系数之间的数值或解析关系。然而，这些方法通常需要波前传感器来获取波像差系数，这在无波前传感器的光学系统中限制了其应用。 近年来，研究者们开始探索不依赖波前传感器的计算方法。其中，Oteo等人提出了一种基于点扩散函数(PSF)质心位置信息的计算方法，而孙敬伟等人则通过分析装配误差与离焦星点图外轮廓的关系，提出了适用于反射望远镜的装调方法。李敏等人利用成像清晰度函数提出了望远镜的在线校正方法，Ju等人研究了彗差和像散对PSF几何特征的影响，从而发展出一种基于图像的波前传感方法，适用于子镜拼接光学系统的装调。 在光学检测中，星点检验法是一种快速、灵敏的装配误差检测手段，但其效率和效果往往取决于检测人员的经验。本文提出了一种基于椭圆度分布的CAA方法，旨在解决这一问题。该方法基于矢量像差理论，推导了星点图与装配误差之间的非线性函数关系，利用椭圆度参数作为特征指标，取代了人为经验，实现了装配误差的量化分析。这种方法只需要通过CCD或CMOS等图像传感器获取星点图像，无需测量波像差，极大地简化了计算过程，具有较高的工程应用价值。 矢量像差理论由Shack和Hopkins奠定基础，他们将波像差从标量形式转化为矢量形式，便于分析失调光学系统的像差场特性。Thompson进一步发展了这一理论，引入视场偏心矢量，用于描述失调系统中的像差变化。通过失调光学系统的波像差矢量形式，可以解析分析装配误差对波像差系数的影响，但直接求解这类方程较为复杂。 本文不直接求解失调方程，而是将装配误差视为黑匣子，通过构建波像差与装配误差之间的关系函数，以椭圆度参数作为关键特征，简化了计算过程。这种方法允许直接利用星点图像，避免了波前传感器的使用，提高了计算的便捷性和实用性，尤其适合于光学系统装调的工程实践。未来，随着智能制造技术的发展和对装调效率的需求增加，这种基于椭圆度分布的CAA方法有望成为光学系统装调的重要工具。