没有合适的资源?快使用搜索试试~ 我知道了~
地铁永磁牵引系统复矢量电流环稳定性研究.docx
1.该资源内容由用户上传,如若侵权请联系客服进行举报
2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
版权申诉
0 下载量 65 浏览量
2022-12-15
14:26:15
上传
评论
收藏 1.51MB DOCX 举报
温馨提示
地铁永磁牵引系统的核心是内置式永磁同步电机(IPMSM),因其高效能和快速响应等特性在轨道交通中广泛应用。然而,IPMSM的非线性和耦合性导致控制难度增加,特别是在高速运行时,耦合效应加剧,影响电流环的稳定性。为了解决这个问题,研究者们采用了复矢量的分析方法来建立电机和电流控制环的模型。 复矢量电流调节器的设计基于零极点对消原理,通过引入随电机转速变化的复零点来抵消模型中的耦合项,实现定子电流励磁分量和转矩分量的有效解耦。这样不仅能改善电流环的耦合特性,还能提升整个系统的控制性能。 然而,地铁永磁牵引系统的特殊性,如大功率、低开关频率、复杂的运行工况,以及在恶劣线路条件下的稳定性要求,使得开关频率的降低会加剧延时效应,恶化电流环解耦性能,可能破坏系统稳定性。文献中提到,通过角度补偿和离散控制器的设计,可以在一定程度上消除数字控制延迟的影响,实现高速条件下的解耦控制。 文章深入探讨了在地铁永磁牵引系统应用背景下的低载波比和变速运行条件对IPMSM复矢量电流调节器稳定性的影响。推导了基于复矢量电流控制器的电流环闭环传递函数,分析数字延时对系统稳定性的影响,并确定了稳定边界条件。接着,通过对永磁同步电机机械运动方程的线性化,推导了系统闭环传递函数,通过绘制零极点分布图,分析不同工况下的稳定边界。 实验验证了所提出的稳定边界条件的准确性和有效性,为地铁永磁牵引系统在实际应用中提供了理论指导,有助于优化控制策略,提高系统的稳定性和效率。通过这样的研究,可以更好地理解和解决IPMSM在复杂运行环境下的控制问题,确保地铁系统的可靠运行。
资源推荐
资源详情
资源评论

1 引言
随 着 内 置 式 永 磁 同 步 电 机 (Interior permanent magnet synchronous
motor,IPMSM)驱动技术的发展,IPMSM 因其功率密度高、电流响应快、转矩脉
动低等优点被轨道交通等领域广泛使用。但 IPMSM 具有非线性、强耦合的特
点,dq 轴系下的 IPMSM 数学模型,含有交叉耦合项,且随着电机转速的升高,耦
合影响加剧,严重影响了控制性能
[1-2]
,为消除交叉耦合项的影响,可用复矢量的
分析方法对 IPMSM 及电流控制环进行建模,并利用零极点对消原理设计复矢
量电流调节器,通过引入随速度变化的复零点抵消电机模型中的复极点耦合项,
实现了对定子电流励磁分量和转矩分量的有效解耦,从根本上改善了电流环的
耦合特点
[3-4]
。
对于地铁永磁牵引系统,其具有以下特点:① 牵引变流器功率大、开关频
率低、电压利用率高、脉宽调制(Pulse width modulation, PWM)技术特殊;②
牵引电机运行工况复杂、变频范围宽、电机参数多变、转矩控制难度大;③ 牵
引电传动系统在复杂、恶劣的线路运行条件下稳定性要求高。为降低开关损耗,
保证散热,提升逆变器效率,开关频率往往限制在 1 kHz 以内。研究指出随着开
关频率的降低会使延时效应加剧,在电流环控制回路中引入相位滞后,进一步加
剧耦合效应的影响 ,恶 化电流环的解耦性能 ,从而降低系统的控制性能,甚至破
坏系统稳定性
[5-6]
。为解决这一问题,文献[7-8]在同步旋转坐标系下,建立了永磁
同步电机及其电流控制环的闭环传递函数,利用根轨迹法分析了数字控制延时
对稳定性的影响,并引入了角度补偿消除了数字控制延迟的影响。文献[9-10]注
意到离散控制器处理数字控制延时的优势,在离散域下建立了永磁同步电机的
数学模型,并设计了复矢量 PI 电流调节器,分析了信号采样延迟和 PWM 发波延
迟的影响,实现了在高速条件下的 d 轴和 q 轴电流分量的解耦控制,改善了运行
在低载波比条件下 IPMSM 的控制性能。
然而,上述研究中未考虑到在地铁永磁牵引系统的应用背景下,载波比低以
及变速带载的复杂工况,因此,本文将探究其对 IPMSM 复矢量电流调节器稳定
性的影响并给出稳定性边界条件。据此,本文在第 2 节中首先推导了基于复矢
量电流控制器的 IPMSM 电流环闭环传递函数,其次在第 3 节中,依据电流环闭
环传递函数分析了数字延时对控制系统稳定性的影响,并给出了稳定边界条件。
然后在第 4 节中,线性化永磁同步电机机械运动方程,推导了系统闭环传递函数,

绘制其零极点分布图,并分析了不同工况下的稳定边界条件。最后在第 5 节中,
测试验证了所推导的稳定边界条件的准确性。
2 电流环-IPMSM 建模分析
2.1 IPMSM 复矢量 控制数学模型
考虑到 IPMSM 在 dq 轴下定子电压方程不对称的特点,采用磁链方程
{ud=Rsid+sψd−ωeψquq=Rsiq+sψq+ωeψd{ud=Rsid+sψd−ωeψquq=Rsiq+s
ψq+ωeψd
(1)
为保证矩阵的对称性,忽略电阻压降和 ω
e
φ
f
项,得到 IPMSM 模型,其复矢量
形式表示为
[11-12]
GP=idqu′dq=1Ldq(s+jωe)GP=idqudq′=1Ldq(s+jωe)
(2)
式中,u'
dq
=u
d
+ju
q
,i
dq
=i
d
+ji
q
,u
d
为定子电压的 d 轴分量;u
q
为定子电压的 q 轴分
量;i
d
为定子电流的 d 轴分量;i
q
为定子电流的 q 轴分量;ω
e
为电机的电角速度;L
dq
为定子电感;φ
f
为永磁体磁链。
由式(2)可知,IPMSM 近似为感性负载,且随着 ω
e
的上升,dq 轴耦合加剧,进
而影响电流环控制性能,甚至破坏控制系统稳定性。
为保证电流环良好的解耦效果,采用零极点对消原理,复矢量电流调节器传
递函数为
Gv=KpLdq(s+jωe)sGv=KpLdq(s+jωe)s
(3)
式中,K
p
为控制器系数。最后在控制器输出补偿电阻压降和 ω
e
φ
f
项便可以
得到实际的控制输出。
在数字控制系统中,存在由模数转换、数字处理器计算和 PWM 发生器
[13]
而
产生的时间延迟。对于对称规则调制,从采样时刻到更新时刻
[14]
持续 1 个载波
周期 T
s
,零阶保持效应使更新后的占空比保持不变,近似于一半 T
s
[15]
,因此总的
延迟可近似为 1.5T
s
[16]
。由数字控制引起的控制延时和采样延时可表示为
Gt=exp(−sTd)≈1Tds+1Gt=exp(−sTd)≈1Tds+1
(4)
式中,T
d
为逆变器的开关周期。
在低载波比情况下,电机控制中坐标变换时所采用的电角度经过采样、计
算延迟已经与真实电角度存在角度滞后,再经过 SVPWM 生成电压矢量作用到
控制器时,此时 dq 轴已旋转角度 θ
d
,即采样时 dq 轴与电压矢量实际作用时 dq
轴之间的夹角为数字控制延时导致的角度延迟。对于矢量控制由于控制延时而
在坐标变换中引入的角度延迟,可表示为
Gd=exp(−jθd)Gd=exp(−jθd)
(5)
式中,θ
d
=ω
e
T
d
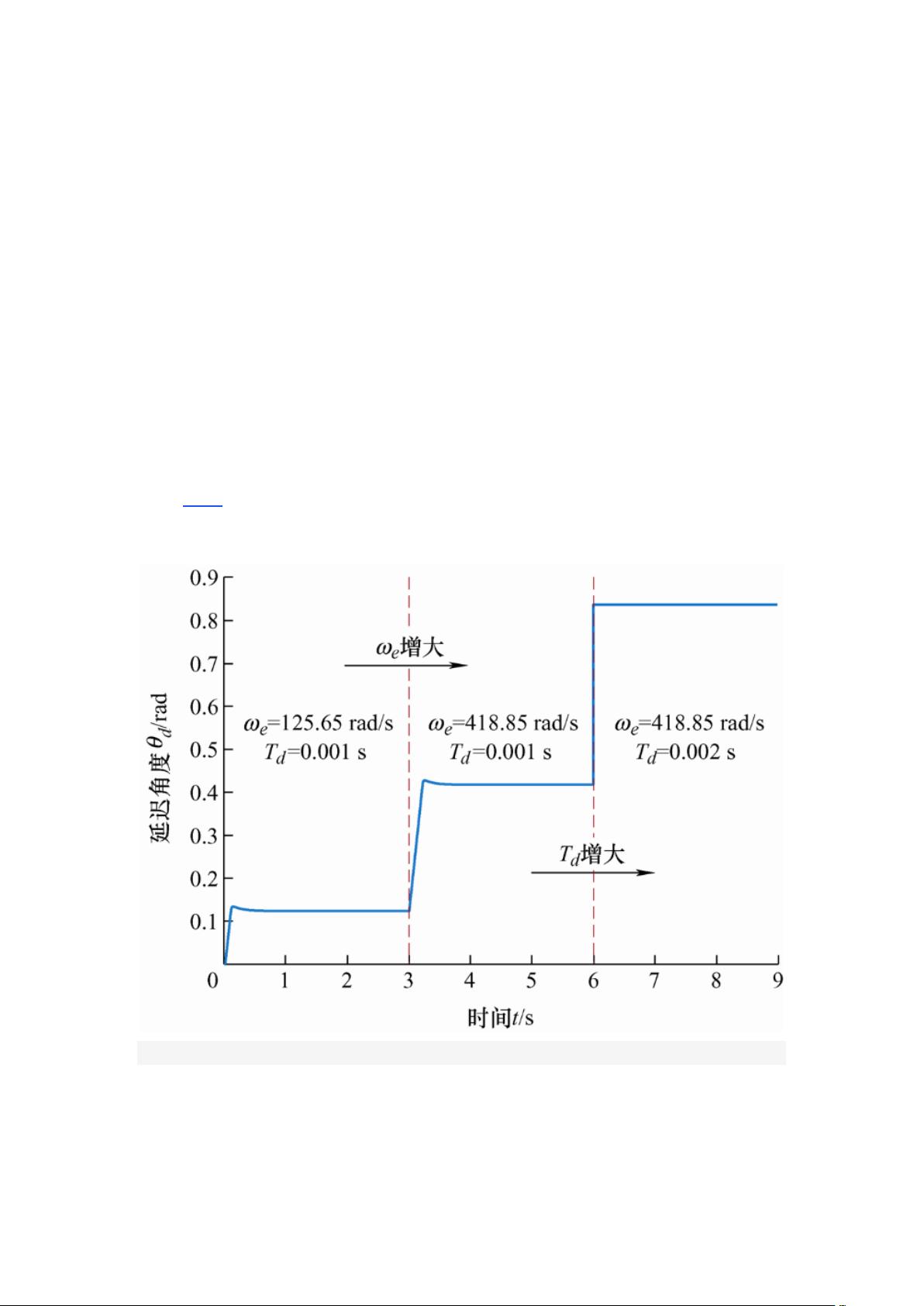
,为延迟角度。其受到电机的电角速度和逆变器开关周期的影
响,如图 1 所示,随着 ω
e
和 T
d
的增大,延迟角度增大。
图 1
图 1 ω
e
和 T
d
对延迟角度的影响
以两相静止坐标系和两相旋转坐标系变换为例,由于延迟角度的影响,可表
示为
uα=udcos(θ−θd)−uqsin(θ−θd)=ud(cosθcosθd+sinθsinθd)−uq(sinθcosθ
d−cosθsinθd)uα=udcos(θ−θd)−uqsin(θ−θd)=ud(cosθcosθd+sinθsin
θd)−uq(sinθcosθd−cosθsinθd)
(6)
由式(6)可知,随着低开关频率引起的角度延迟的增大,导致 dq 轴耦合加剧,
进一步影响电流环控制性能。
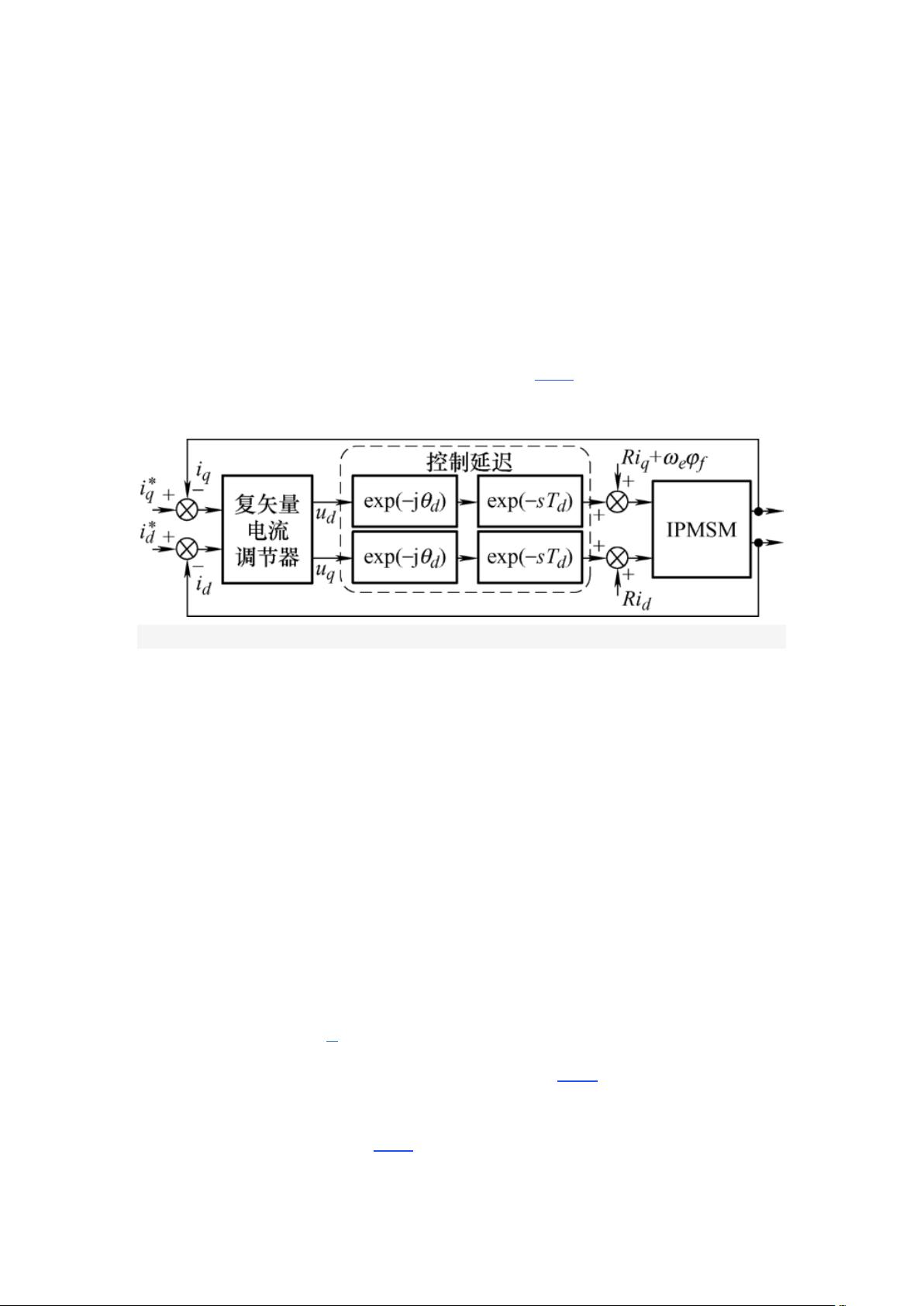
综上,IPMSM 复矢量电流调节器控制框图如图 2 所示。
图 2
图 2 IPMSM 复矢量控制框图
2.2 动态 解耦性能分析
如基于 复 矢 量 的 电流环 控 制 框 图 所示,在不考 虑 控 制 延 时的情 况 下 ,由 式
(2)、(3)得到,系统闭环传递函数为
Gvp=GvGP1+GvGP=Kps+KpGvp=GvGP1+GvGP=Kps+Kp
(7)
由式(6)可知,由于在电流控制器的传递函数中引入了与 IPMSM 交叉耦合
项相同的复零点,与电机模型中的复极点对消,使系统闭环传递函数中不再含有
耦合项,并化简为一阶惯性环节,其带宽由控制器参数 K
p
决定。通常为保证控制
器性能,选择 K
p
≤0.1/T
d
[17]
。
为直观展现零极点的变化规律,根据式(7)以及表 1 所示的电机参数,给定
K
p
=10,画出电角速度 ω
e
由 0 rad/s 上升至 754 rad/s 时,系统闭环传递函数零极
点随转速变化的零极点图,如图 3 所示,图中“×”表示极点,“○”表示零点。
剩余22页未读,继续阅读
资源评论

罗伯特之技术屋
- 粉丝: 4457
- 资源: 1万+

下载权益

C知道特权

VIP文章

课程特权
开通VIP
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功