没有合适的资源?快使用搜索试试~ 我知道了~
基于因果生成神经网络的因果特征发现与预测.docx
1.该资源内容由用户上传,如若侵权请联系客服进行举报
2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
版权申诉
0 下载量 66 浏览量
2022-06-19
11:35:53
上传
评论
收藏 941KB DOCX 举报
温馨提示
基于因果生成神经网络的因果特征发现与预测.docx
资源推荐
资源详情
资源评论

引言
机器学习正在成为医疗保健领域越来越重要的技术手段。一些基于机器学习算法的人工智能系统在癌
症分类检测
[
]
、糖尿病视网膜病变检测
[
]
方面的水平已经接近甚至超过了人类专家。毫无疑问,人
工智能将重塑医学的未来。然而,目前已成功应用于医疗问题的机器学习方法仅基于关联而非因果关
系 。 在 统 计 学 中 , 关 联 在 逻 辑 上 并 不 意 味 着 因 果 关 系
[
]
。 相 关 性 与 因 果 关 系 之 间 的 关 系 由
[
]
正式确定为共同原因原则,即如果两个随机变量 和 在统计上相互依赖,则必须
持有以下因果解释之一:① 是 的直接原因;②有一个随机变量 是 和 的共同原因。因此,与
关联相比,因果关系进一步探索了变量之间更本质的关系。
随着现代医学技术的飞速发展,针对患者采集的临床数据越来越多,这种增长对疾病预测模型的性能
以及检测效率均提出了巨大挑战。理论上使用的特征越多,模型训练效果越好,而在测试集中效果不
理想的现象可解释为非相关特征过度拟合,导致模型性能和泛化能力降低。但事实上,变量越多并不
意味着信息越有用,预测效果越好。因此,为了减小数据集规模、提高模型预测性能,减少特征数量
非常必要。在机器学习中,特征选择是获得良好预测效果的重要步骤之一。近年来,人们不仅对基于
信息选择特征进行预测感兴趣,还希望了解这些特征与研究目标的相互作用。在这种背景下,一些研
究者开发了一些理论,试图将图()与因果关系的概念引入到特征选择中,目的是找到能够生
成数据的因果关系,以便更好地理解数据集的底层机制。以癌症为例,我们需要知道其是什么原因导
致的,需要使用哪些变量治愈。
相关研究
因果特征选择作为一种新兴的特征滤波方法,其为特征与类属性之间的关系提供了因果解释,从而更
好地理解数据背后的机制。与非因果特征选择相比,因果特征选择在理论上是最优的,回答了最优特
征选择包含哪些核心特征,以及特征滤波方法在什么条件下能够输出最优特征的问题。
传统的因果特征选择是在因果贝叶斯网络( !",)中寻找类属性的马
尔可夫毯(#"!$",#),其中边 % 表示 为 的直接原因(父亲节点), 为 的
直接结果(孩子节点)。目标变量(例如类标签)的 # 由父节点、子节点以及子节点的父节点(配
偶节点)构成。# 提供了围绕局部因果结构的完整结构,即 # 是最小的特征集,其使类属性在统
计上条件独立于所有的其他属性
[
&
]
。在该研究领域,'! 等
[
(
]
首先引入 # 进行特征选择,并提
出 '!)*('))算法,但 ') 算法并不能保证找到真正的 #;#+ 等
[
,
]
设计了一
种 )(! +)"+)算法,可用于贝叶斯网络结构学习;-*.! 等
[
]
改良了 )
算 法 , 并 提 出 一 系 列 用 于 最 优 特 征 选 择 的 # 发 现 算 法 , 从 而 形 成 了 /0# ( /*
0!!.#)算法家族,包括 /0#、/0#、/0#1
[
]
和 2/0#
[
]
等;
!. 等
[
]
提出因果生成神经网络( $ !" ,),利
用条件独立性和分布不对称性探索双变量和多变量的因果结构; ' 等
[
]
提出结构不可知
建模 ()0+!#!.+,)0#)方法,该法基于不同参与者之间的博弈,结合分
布估计、稀疏性和非循环性约束的学习准则,通过随机梯度下降方法进行端到端的参数学习。
本文参考文献[][]的研究成果,提出一种基于生成神经网络和强化学习的因果特征选择和
预测模型,框架如图 所示。该模型包含一个因果门网络和一个因果预测网络,其中因果门网络输入
原始数据,输出选择因果概率,然后根据这些概率对选择向量进行采样;因果预测网络接收所选特征
并进行预测。两个网络基于真实标签进行反向传播的训练,然后从预测网络的损失中减去基线网络损
失,用于因果门网络的更新。
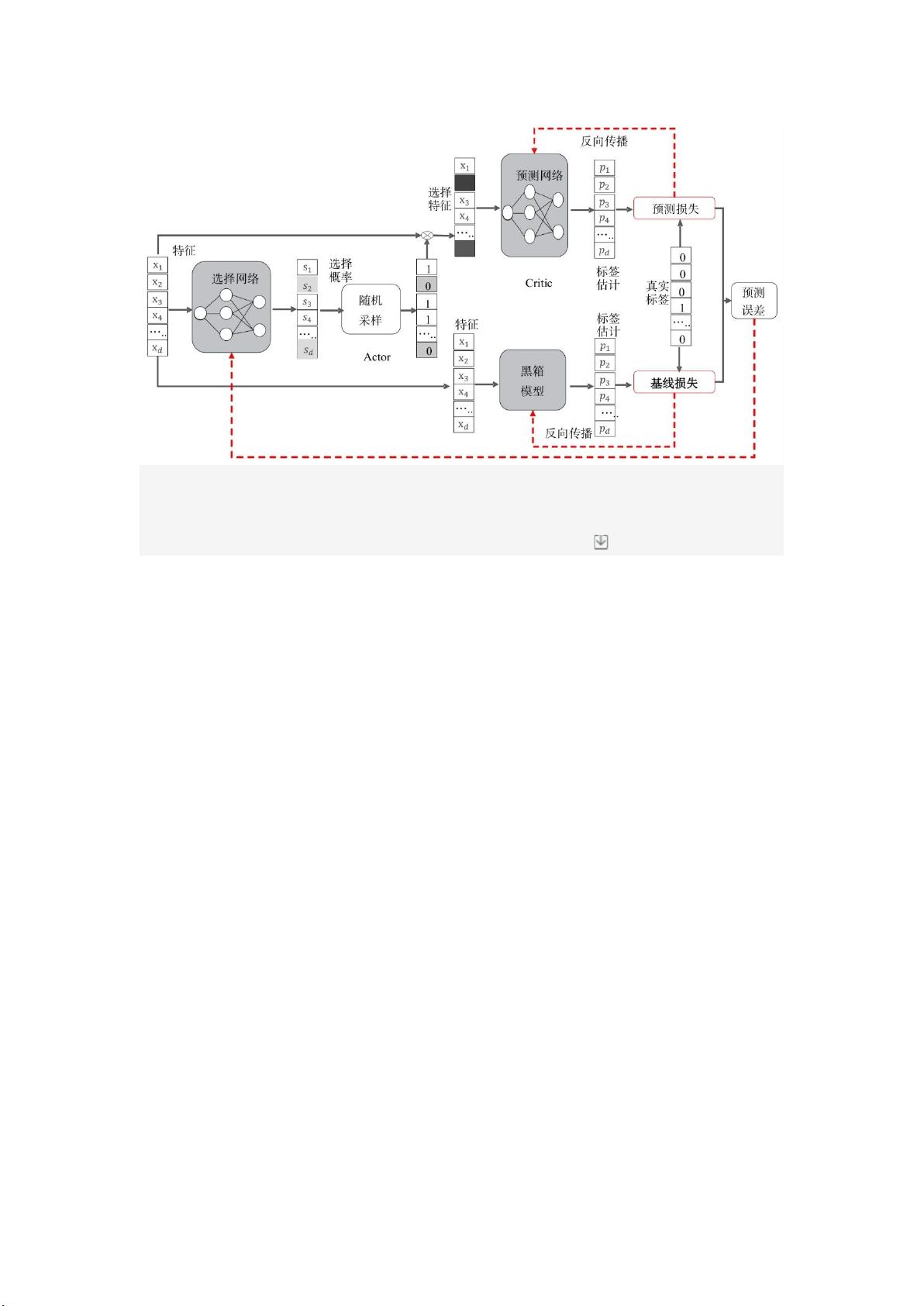
图 1本文模型框架
Fig. 1The proposed model framework
下载34原图 54高精图 54低精图
因果模型
设 6789.8.:; , 表 示 .: 维 随 机 变 量 向 量 ; P
(
X
)
为 联 合 概 率 分 布 ; <678
98.8.:;,表示 d 个随机特征空间变量向量;.: 为离散的标签空间变量。基于观察因果发
现 从 分 布 P
(
X
)
中 采 集 独 立 同 分 布 的 样 本 =6>?@898?A@898?@B , ?A@6?A89
A.8A.:@。为了更清楚地表示患者数据,将 .: 表示为患者的疾病标签 。
C 函数因果模型
数据的底层生成模型假设为函数因果模型
[
]
,定义为一对(,D),其中 为一个有向无环图;
D6?D89D.8D.:@,为一组 .: 的因果机制。函数因果模型假设每个变量满足如下关系:
A6DA??A8@8EA@44 44EA4F?8@44D!4A689.8.:A6DAA88EA44
A689.8.:
式中, 为图 中的一个变量;(A,)为 的父节点;DA 为函数:?5?A8@5:@%; EA 为
高斯噪声。在 上的函数因果模型如图 所示。
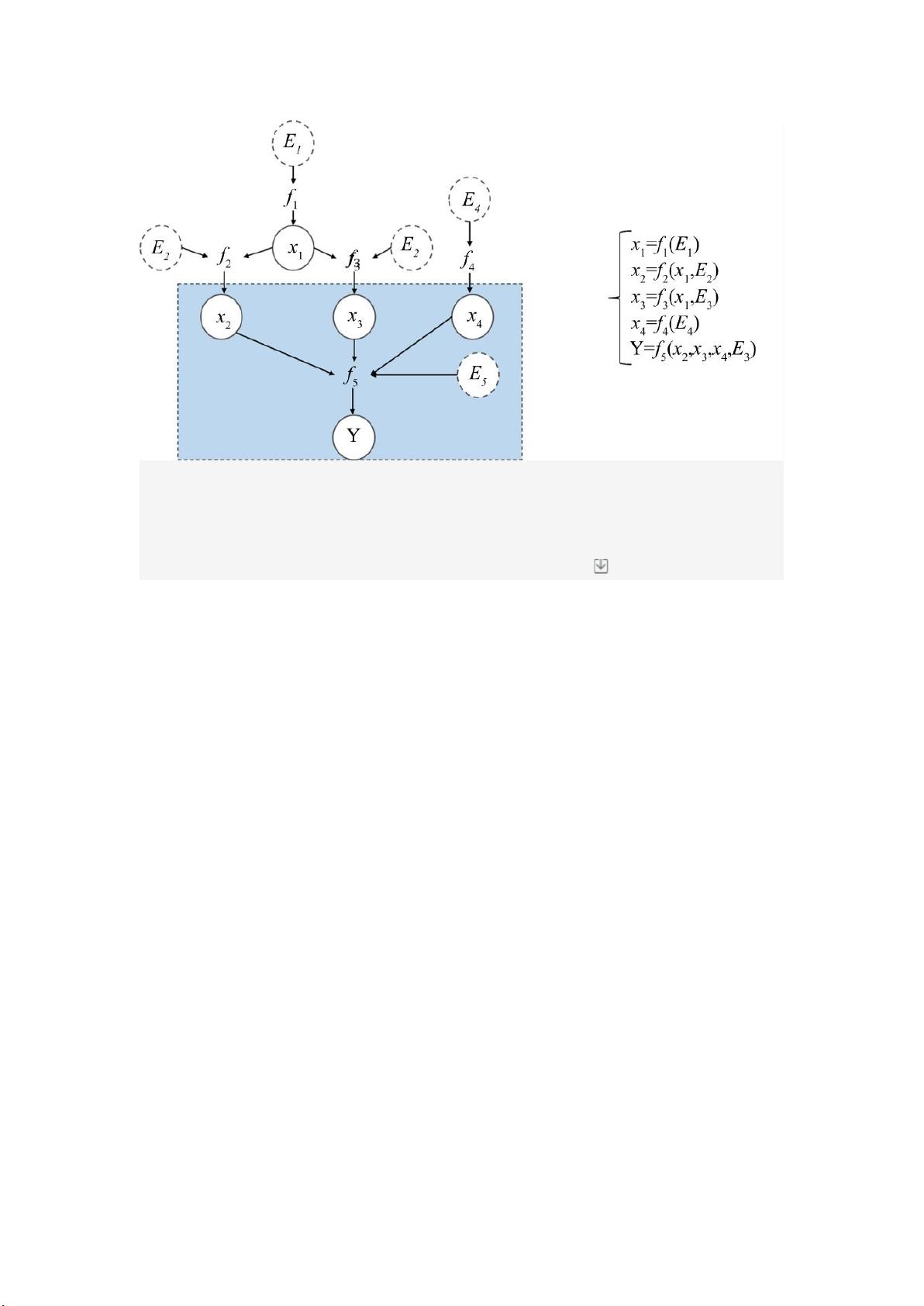
图 2在 X 上的函数因果模型示例(左:因果图,右:因果机制)
Fig. 2Example of functional causal model on X(Left: causal graph G;
Right: causal mechanisms)
下载34原图 54高精图 54低精图
C 深度神经网络的因果机制
通用近似定理
[
,
,
]
指出:具有单个隐藏层的标准多层前馈网络中包含有限数量的隐藏神经元,是对
紧凑子集上连续函数中激活函数轻微假设情况下的通用逼近器。因此,本文基于函数因果模型和神
经网络通用近似定理,利用神经网络拟合函数 D.:。
如图 所示,深层神经网络的因果机制由 G 隐层神经网络实现,其中 A6?8898.@为因果系数。
如果使用变量 A 生成 ,即 A% 在图 中有一条边,因此认为 A 为 的原因,A 为 ,否则 A 为
;EA 为高斯噪声。网络结构的数学表达式为:
6D?8E@6HG:IHGI99H?7J8E;@6D8E6HG:IHGI99H?7
式中,J 表示两个向量之间对应元素相乘,7J8E;为连接 J 和噪声的 .: 维向量,H 为隐
层中的代数变换。
剩余11页未读,继续阅读
资源评论

罗伯特之技术屋
- 粉丝: 4506
- 资源: 1万+

下载权益

C知道特权

VIP文章

课程特权
开通VIP
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- dd061-main.zip
- OpenArk64-1.3.8beta版-20250104
- 带头双向循环链表C语言实现源代码.zip
- FOC矢量控制 手把手教学,包括FOC框架、坐标变、SVPWM、电流环、速度环、有感FOC、无感FOC,霍尔元件,卡尔曼滤波等等,从六步向到foc矢量控制,一步步计算,一步步仿真,一步步编码实现功能
- comsol超快激光表面处理双温模型 三维 二维轴对称的 光束可整形
- whynotwin11(windows11升级检测工具)
- 硬件工程师知识体系脑图
- 基于污水再生全流程的AO除磷工艺研究:工艺优化与群落结构分析
- 使用MATLAB自主编程实现凝固CET转变 柱状晶转变等轴晶 实现经典的Karma模型 适用于激光烧蚀融覆,激光增材制造,激光切割,激光焊接,等等凝固显微组织模 能够看到枝晶臂粗化,溶质富集,枝晶竞争
- yolov311111111111111111111
- MFC小游戏十一:主对话框界面
- 恢复WIN11经典右键菜单和取消任务栏文件资源管理器 字样
- 基于matlab的轴承的润滑方程进行数值求解仿真,改变偏心率和宽径比,可求输出不同参数下的油膜压力,厚度等的分布情况,并且输出承载力和摩擦力变化趋势 程序已调通,可直接运行
- influxdb-1.7.11-linux-arm64.tar.gz
- QT GraphicsView 简易图元编辑器
- STM32开发板的调试及串口显示实验结果分析与应用验证
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功