1.1 考虑硬件友好和网络小巧的设计思路
1.1.1 填充方式的确定
这里首先设卷积核尺寸为 K×K,图像尺寸为 R×C,以便后续定量的分析不同
填充方式所需填充的层数、输出图像的尺寸以及卷积核的移动范围(这里 R=5,C=5,
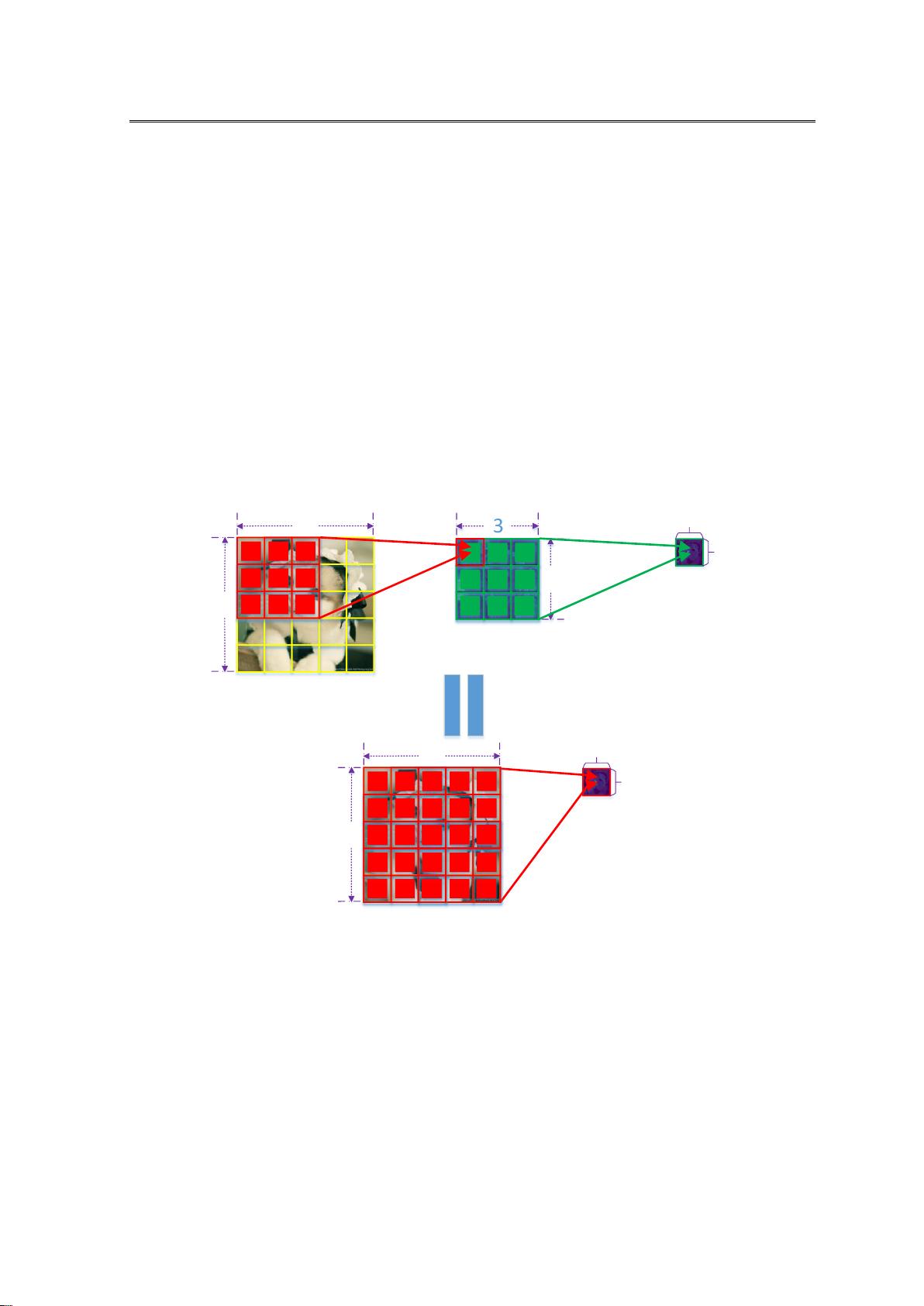
K=3)。 图 1.1 (a)、(b)、(c)分别展示了“FULL”、“VALID”及“SAME”三种不同填
充方式下卷积核的可移动范围,其中红色部分为卷积核,黄色部分为图像,绿色部分
为填充值 0(为了不影响原来的图像像素信息,一般填充 0 值)。
(1). “FULL”方式:
如图 1.1(a)所示,在“FULL”方式下,当卷积核和图像刚刚接触时,卷积操作便
开始了。此种方式需在原有图像基础上向上下左右各填充 K-1 维的 0 值来保证卷积操
作正常执行。完成卷积操作后,其输出特征图的尺寸为(R+K−1)×(C+K−1)。
(2). “SAME”方式:
“SAME”方式的意思是当卷积运算的步进为 1 时,其输出特征图尺寸与输入图
像尺寸相同,如图 1.1 (b)所示。为保证卷积运算的运行,也需要在原图基础上进行 0
值的填充,但“SAME”模式会尝试向左或向右均匀地填充 K−1 列的 0 值,即将会在
左方填充⌊(K−1) ∕2⌋列 0 值,在右方填充(K−1)−⌊(K−1) ∕2⌋列 0 值(其中⌊ ⌋表示向下取整
操作,另外向上向下的填充方式与向左向右类似)。
(3). “VALID”方式:
而在“VALID”方式下,如图 1.1 (c)所示,只有当卷积核的所有权值参数全部滑
动进入图像内部时,卷积操作才开始。不难看出,其卷积核的移动范围更小,但此种
方式并不需要对原图进行任何填充操作,而其输出特征图的尺寸为(R−(K−1))×
(C−(K−1))。