
题目
摘要
关键词(黑体不加粗小四号):

一、问题重述
1.1 问题背景
中国作为世界上最大的发展中国家,能源消耗逐年以惊人的速度增长,如何实现环境可持续
发展成为了全国上下的一致呼声。而建筑作为能耗大户,其节能效益的提升显得尤为重要。
光伏建筑一体化【1】(BIPV)是一种将太阳能发电(光伏)产品集成到建筑上的技术,具有
建筑节能、绿色环保、不占用土地、节省投资的优点,对建筑环保有着至关重要的作用。近
年来,光伏建筑一体化得到国家政策的大力推动:2003 年,北京市大兴区“屋顶型光伏网示
范电站”是国家科技部“十五”科技攻关项目;2004 年,深圳建成目前亚洲最大的并网太阳能
光伏电站,设计及安装与深圳综合展馆、花卉展馆等建筑融为一体,堪称国内绿色建筑的典
范;北京南站中,主站房屋面中央采光带也采用了太阳能光伏发电系统,该系统总发电量约
320 千瓦,可辅助解决车站的用电问题;中国首个彩色透光薄膜组件应用示范项目——天威
薄膜光伏建筑一体化项目也已经顺利通过国家级验收。作为庞大的建筑市场与光伏市场的结
合点,光伏建筑一体化必将存在着无比光明的发展前景,具有巨大的市场潜力。
中国证券市场【2】从 1870 年至今已有 120 多年的历史,是国有企业股份制的改革产物。
中国股市刚刚开张之时,上市交易的只有沪市的“老八股”和深市的“老六股”,总市值不过 20
多亿元,但截至 2020 年底,两市上市公司家数已经达到 4100 家;其中 A 股上市公司数突
破 1000 家是在 2000 年,2010 年突破 2000,2016 年突破 3000,2020 年 9 月突破 4000 家。
中国股市在近几十年来发生着翻天覆地的变化。除了促动投资、就业、出口、消费以外,股
票还可以对行业运营态势与发展前景作分析与预测。分析股票板块市场的走势,是把握行业
发展趋势,洞悉行业竞争格局,规避经营和投资风险,制定正确发展战略的重要工具。
如何利用光伏建筑一体化板块的股票数据建立预测模型与相关性模型,并给出合理的投资建
议,从而得出我国光伏建筑一体化行业未来发展的趋势,是本文探讨的重点问题。
1.2 需要解决的问题
光伏建筑一体化是实现建筑环保的有效途径,通过股市走势可以对该板块指数发展做出分析
及预测,根据附件给出的沪深股市 37 家光伏建筑一体化相关企业股票数据,对其发展趋势
作出分析:
(1)、绘制 2019 年 4 月 1 日至 2021 年 4 月 30 日该板块指数的移动平均线。
(2)、利用 2021 年 5 月 6 日至 5 月 28 日数据进行误差分析并修正模型,对本版块未来发
展趋势做出预测,给出移动平均线。
(3)、利用 2019 年 4 月 1 日至 2021 年 4 月 30 日数据对上证指数和光伏建筑一体化板块指
数进行相关性分析。
(4)、给出 2021 年 6 月份该板块最优投资方案。

二、问题分析
本文要解决的是通过板块指数做出发展趋势的分析及预测问题,问题一、二要求对股票原始
数据进行处理并给出移动平均线,预测发展趋势,问题三需进行上证指数与光伏建筑一体化
板块指数的相关性,问题四、五基于上述模型及分析,给出投资方案与行业发展报告。
2.1 问题一的分析
针对问题一,要求给出板块光伏建筑一体化板块指数的移动平均线,分为板块指数计算、移
动平均线计算、可视化图表的绘制三步。
根据附件中给出的 37 家企业的数据,从已定基期出发,计算出题目中所需的各个日期板块
指数。考虑到上市、停市对股市的影响,计算过程中同时对板块指数进行相应的修正。
在得到板块指数的基础上,根据数据特征,采用更能反应股市变动的指数移动平均线,考虑
近期交易日报价对当日移动平均的影响,并引入平滑系数,对每日指数移动均价进行计算。
最后,分别绘制 5 日、10 日、15 日三个周期的指数移动平均线图。
问题二
针对问题二,在问题一得出的光伏建筑一体化板块指数移动平均线的基础上,我们要将这些
离散的点拟合为连续的曲线,并依据 2021 年 5 月 6 日到 2021 年 5 月 28 日的板块指数移动
平均线对拟合模型做出误差分析和调整。依据调整后的模型对日移动平均线、周移动平均线
和月移动平均线做出预测。
考虑到每日的板块指数移动平均线并非相互独立的数据,我们对股票指数的预测是以以往历
史信息为依据的,因此,我们可以将历史信息与当前信息分别赋予一定的权值,以此为依据
进行预测。基于这种思想,我们采用能够记忆历史信息的循环神经网络模型对股票指数进行
拟合并做出预测。
股票的板块指数移动平均线属于典型的时间序列,同时考虑到股票指数走势具有一定的随机
性,为达到更好地拟合效果,我们采用 ARIMA 模型对板块指数移动平均线再次进行拟合,
将循环神经网络模型与 ARIMA 模型的预测值取平均。
问题三
针对问题三,
三、模型假设
1.股市分析以 2019 年 1 月 2 日基期
2.调整只有新增股票进行,而且是在新增股票上市后的半个月之后才进行
3、股票买进,抛出不考虑手续费的影响
四、符号说明
当日收盘价 P
cl
(t)
板块指数 B(t)
报告期股票市价总值 K(t)
基期股票市价总值 G(t)
当日指数移动均价 b
avg
(t)
EMA 平滑系数 ξ

EMA 周期 T
五、模型的建立与求解
5.1 问题一模型的建立与求解
5.1.1 板块指数的计算
根据板块指数计算公式:
B(t)=K(t)÷G(t)× 100
其中:
K(t)= ∑(某支股票市价×总股本)
G(t)= ∑(基期某支股票市价×基期总股本)
我们以 100 为基期指数,基日为 2019 年 1 月 2 日,根据附件中给出的 37 家光伏建筑一体
化企业,就可以计算出该板块自 2020 年 1 月 3 日至 2021 年 5 月 27 日的板块指数,并存于
表格中备用。
5.1.2 板块指数的修正
为了剔除新股上市等非交易性因素对指数的影响,在计算板块指数时,基期股票总市值会按照
一定规则,不断进行修正。根据各大证券交易所的指数修正规则,我们采用“除数修正法”修正。
即认为修正后的基期股票市价总值=(修正前的报告期股票市价总值+新增或者减少的股票
市价总值)×修正前的基期股票市价总值÷修正前的报告期股票市价总值。
以该修正后的基期股票市价总值作为以后指数计算的基期股票市价总值,即新基期。
5.1.3 指数移动平均线
移动平均线(MA),是用统计分析的方法,将一定时期内的证券价格(指数)加以平均,并
把不同时间的平均值连接起来,形成一根 MA,用以观察证券价格变动趋势的一种技术指标。
指数移动平均线(EMA)是在普通移动平均线的基础上改进,其特殊点在于,EMA 赋予不同交
易日的报价的不同权重,报价离当前越近,权重越大,对移动均线的走势影响也越大。
指数移动平均线的计算公式如下:
b
avg
(t)
n
=( P
cl
(t)- b
avg
(t)
n-1
)* ξ+ b
avg
(t)
n-1
其中,根据经验公式,取 ξ=2/(1+T),T 为 EMA 周期,即题目中要求的 5 日、10 日、20 日。
通过上述公式,分别计算出 T=5、10、20 时的当日指数移动均价,记录在表格中并绘出可
视化图表如下:
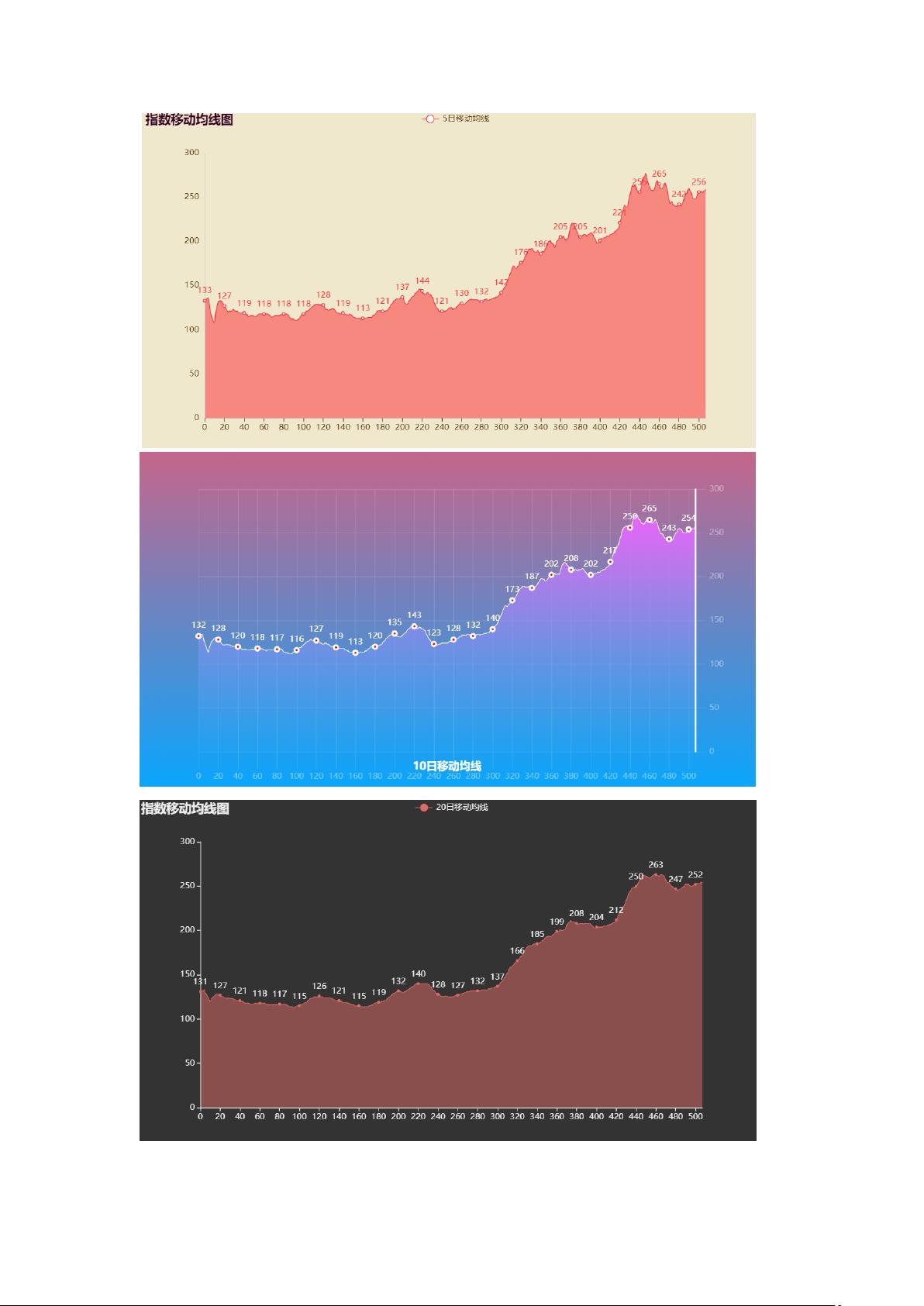
当行情发生快速、剧烈的波动时,EMA 更能反映近期价格波动的情况,对于本题板块指数















