没有合适的资源?快使用搜索试试~ 我知道了~
fpe算法过程实例和算法实现原理
资源推荐
资源详情
资源评论

The FFX Mode of Operation for
Format-Preserving Encryption
Draft 1.1
Mihir Bellare
1
Phillip Rogaway
2
Terence Spies
3
February 20, 2010
1 Introduction
This specification document describes FFX, a mechanism for format-preserving encryption (FPE).
Schemes for FPE enable one to encrypt Social Security numbers (SSNs), credit card numbers
(CCNs), and the like, doing so in such a way that the ciphertext has the same format as the
plaintext. In the case of SSNs, for example, this means that the ciphertext, like the plaintext,
consists of a nine decimal-digit string. Similarly, encryption of a 16-digit CCN results in a 16-digit
ciphertext. FPE is rapidly emerging as a useful cryptographic tool, with applications including
financial-information security, data sanitization, and transparently encrypting fields in a legacy
database.
The encryption algorithm of FFX takes in a key K, a plaintext X,and a tweak T . The plain-
text is taken over an arbitrary alphabet Chars. Assuming that n = |X| is a supported length,
FFX.Encrypt will produce—deterministically—a ciphertext Y = FFX.Encrypt
K
T
(X) ∈ Chars
n
.
One can recover X from Y by way of X = FFX.Decrypt
T
K
(X).
FFX mode is flexible and customizable. In particular, unrepresented in the explicitly named argu-
ments to FFX.Encrypt and FFX.Decrypt is the fact that FFX depends on a number of parameters.
Once chosen, it is assumed that they are held fixed for the lifetime of a given user-generated key.
The parameters used in FFX include the number of Feistel rounds rnds(n), the desired degree of
imbalance split(n) in the Feistel network, and the round function F.
As example instantiations of FFX, we consider enciphering (i) binary strings of 8–128 bits, or
(ii) decimal strings of 4–36 digits. In Appendices A and B we specify parameter sets, denoted A2
and A10, to enable these task. Both employ a round function derived from AES. The fully instan-
tiated schemes would be denoted FFX-A2 and FFX-A10.
1
University of California, San Diego, Dept. of Computer Science & Engineering, 9500 Gilman Drive, La Jolla,
CA 92093, USA. e-mail: mihir@cs.ucsd.edu, url: http://cseweb.ucsd.edu/∼mihir/. Bellare’s work on this spec has
been done in collaboration with Semtek Innovative Solutions Corp; please see the acknowledgments on p. 6.
2
University of California, Davis, Dept. of Computer Science, One Shields Avenue, Davis, CA 95616, USA.
e-mail: rogaway@cs.ucdavis.edu, url: http://www.cs.ucdavis.edu/∼rogaway/. Rogaway’s work on this spec has been
done in collaboration with Voltage Security; please see the acknowledgments on p. 6.
3
Voltage Security, 4005 Miranda Ave, Suite 210, Palo Alto, CA 94304, USA. email: terence@voltage.com.
Spies is the Chief Technology Officer at Voltage.
1

2
The name FFX is meant to suggest Format-preserving, Feistel-based encryption. The X reflects
there being multiple instantiations (that is, parameter choices). It further reflects that FFX is an
outgrowth of, and extension to, the FFSEM specification earlier submitted to NIST by Spies [28].
The current draft replaces that contribution. Compared to it, FFX is more general, adding in
support for tweaks, non-binary alphabets, and non-balanced splits. Cycle-walking can now be
avoided in the setting of primary practical importance, encrypting decimal strings.
While this document does not attempt to explain or survey all of the cryptographic results relating
to FFX, their existence—and indeed the entire history of results concerning Feistel networks—
underlies our mechanism’s selection. In general, contemporary cryptographic results and experience
indicate that FFX achieves cryptographic goals including nonadaptive message-recovery security,
chosen-plaintext, and even PRP-security against an adaptive chosen-ciphertext attack. The quan-
titative security depends on the number of rounds used, the imbalance, and the adversary’s access
to plaintext/ciphertext pairs. One assumes that the underlying round function is a good pseudo-
random function (PRF).
While FFX can, in principle, be used to encipher character strings of arbitrary length, the mecha-
nism is intended for message spaces smaller than that of AES (2
128
points). For enciphering longer
strings, other techniques would seem to be preferable. In particular, EME2 [9] can encipher binary
strings of any length n>128.
An earlier version of this specification document, version 1.0, was provided to NIST in November
2009. The substantive change we have made since that version is the addition of a parameter profile
for binary strings, A2.
Definition of FFX
See Figure 1 for an illustration of FFX, Figure 2 for a description of the parameters on which FFX
depends, and Figure 3 for the the definition of FFX in terms of these parameters. We expect all
parameter choices to be fixed for the lifetime of a given key. Encryption and decryption must use
the same parameters.
3Notation
Throughout this document, a number means a nonnegative integer. Plaintexts and ciphertexts
are regarded as strings over an alphabet Chars = {0, 1,...,radix − 1}. Members of the alphabet
are called characters. The number of characters radix in Chars is referred to as the radix of the
alphabet. Example radix values are 2, 10, and 26, corresponding to bits, digits, and uppercase
English letters. It is required that radix ≥ 2.
If a user wishes to encrypt over a non-numeric alphabet, say {a,...,z}, she must set up a bijective
mapping between this alphabet and Chars = {0,...,radix − 1} via which her inputs and outputs
can be regarded as numeric values, as required for our algorithms.
A string is a finite sequence of characters from Chars.By | X | we denote the length of string X,
the number of characters in it. For example, X = 00326 is a string of length | 00326 | = 5. Note
2
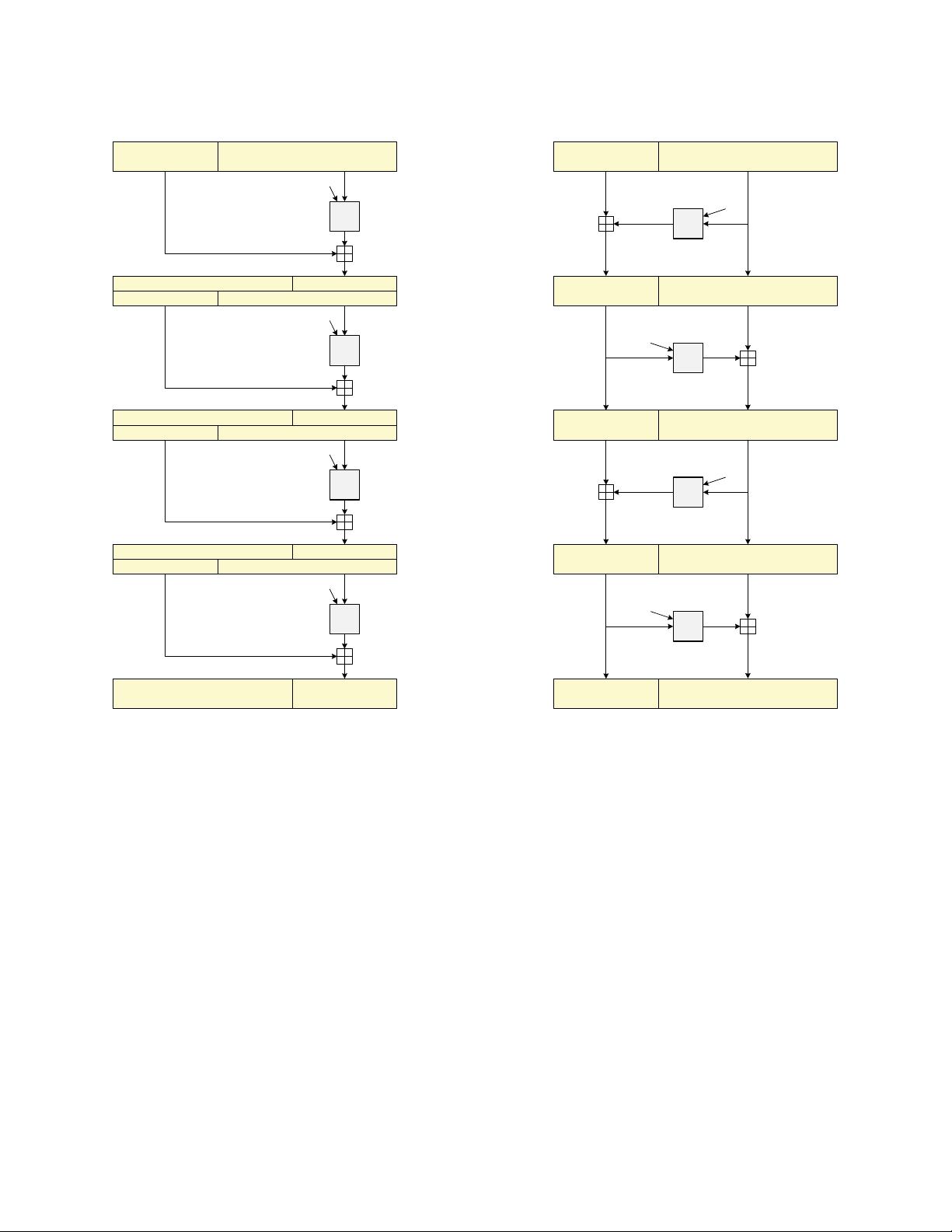
` n − ` ` n − `
A
0
B
0
C
0
B
0
A
1
B
1
n, T , 0
K
F
K
F
C
2
B
2
A
3
B
3
K
F
K
F
C
1
B
1
A
2
B
2
C
3
B
3
`
n, T, 1
A
0
B
0
C
0
= B
1
B
0
= A
1
B
2
= C
1
n, T, 1
A
2
=
B
1
n, T, 0
K
F
K
F
C
2
= B
3
B
2
= A
3
n, T, 3
n, T, 2
K
F
K
F
B
4
= C
3
A
4
=
B
3
n, T , 2
n, T, 3
Figure 1: Illustration of FFX encryption when method =1 (left) and method =2 (right). The
first four rounds are shown. The divided boxes on the left are used to illustrate the re-partitioning of a
string; for example, string B
0
C
0
is exactly the string A
1
B
1
,where |C
0
| = |A
1
| = £ and |B
0
| = |B
1
| = n − £.
No such re-partitioning occurs on the right, but strings get two names instead. All boxed strings are over
Chars = {0, 1,...,radix − 1}, while T is a byte string, n ≥ 2isanumber, and 1 ≤ £ ≤ n − 1 is the imbalance.
that leading zeros are counted just like any other character. By Chars
∗
we mean the set of strings
over Chars having any length. If X, Y ∈ Chars
∗
are strings we let XY or X I Y denote their
concatenation. The i-th digit of a string X will be denoted X[i], for any i ∈{1,...,| X |}.For
1 ≤ i ≤ j ≤|X | we let X[i..j]= X[i] ···X[j].
The function takes a pair of equal-length strings and returns a string of the same length. Two
possibilities are allowed: characterwise addition and blockwise addition. For characterwise addition,
a
1
···a
n
b
1
···b
n
= c
1
···c
n
where c
i
=(a
i
+ b
i
)mod radix. For blockwise addition, c
1
···c
n
is
(
instead the unique string such that c
i
radix
n−i
= a
i
radix
n−i
+ b
i
radix
n−i
)
mod radix
n
.For
example, when radix = 10, characterwise addition would have 439 724 = 153 while blockwise
addition would result in 439 724 = 163. The function correspondingly takes a pair of equal-
length strings and returns a string of the same length. It is determined by saying that X Y is the
3

parameter description
radix The radix,a number radix ≥ 2 that determines the alphabet Chars = {0,...,radix − 1}.
Plaintexts and ciphertexts are strings of characters from Chars.
Lengths The set of permitted message lengths . For a plaintext to be encrypted, or for a ciphertext
to be decrypted, its length must be in this set.
Keys The key space, a finite nonempty set of binary strings.
Tweaks The tweak space, a nonempty set of strings. Conceptually, different tweaks name unrelated
encryption mappings.
addition The addition operator , either 0 (characterewise addition) or 1 (blockwise addition). De-
termines the meaning of the operators X Y and X Y that add or subtract equal-length
strings over the alphabet Chars = {0, 1,...,radix − 1}.
method The Feistel method, either 1 or 2. The value determines which of the two prominent Feistel
variants will be used.
split (n) The imbalance, a function that takes a permitted length n ∈ Lengths and returns a number
1 ≤ split(n) ≤ n/2.
rnds (n) The number of rounds, a function that takes a permitted length n ∈ Lengths and returns
an even number rnds(n).
F The round function, a function that takes in a key K ∈ Keys, a permitted length n ∈
Lengths,a tweak T ∈ Tweaks, a round number i ∈{0,...,rnds(n) − 1},and a string
B ∈ Chars
∗
. It returns a string F
K
(n, T, i, B) ∈ Chars
∗
.If method =1 or i is even then
| B | = n − split(n)and | F
K
(n, T, i, B) | = split(n). If method =2 and i is odd then
= n − split(n).| B | = split(n)and | F
K
(n, T, i, B) |
Figure 2: Parameters of FFX. To have a fully-specified scheme, each of these parameters must be defined.
unique string Z such that Y Z = X. As an example, still with radix = 10, we have 32 15 = 27
for characterwise addition and 32 15 = 17 for blockwise addition. Note that when the radix is
two, characterwise addition and subtraction are the same as xor.
We expect radix and Lengths to be determined by the needs of the application, not by security
considerations. The choice of Keys will typically flow from the underlying cryptographic primitive
employed; for example, the key space might consist of AES keys if one uses AES to construct the
round function. The set Tweaks should be large enough to accommodate all non-secret information
that may be associated to a plaintext. Users are strongly encouraged to employ tweaks whenever
possible, as their judicious use can significantly enhance security. See Appendix F. The addition
parameter specifies the group over which addition is performed. Efficiency considerations determine
its choice; we do not expect the value to be security relevant.
In specifying a collection of parameters one must choose rnds,as well as method and split,in order to
balance performance requirements and security considerations. See Appendix H for a discussion.
To avoid known attacks, we require that rnds(n) ≥ 8if n =2 · split(n)orif method = 2 and
n =2 · split(n) + 1, and we require that rnds(n) ≥ 4n/split(n) otherwise. We emphasize that these
values are minimums, not recommended values. We insist that radix
n
≥ 100. This last requirement
is to prevent the meet-in-the-middle attack discussed in Appendix H.
The round function F
K
(n, T, i, B) must be constructed from a blockcipher E or a hash func-
tion H. We recommend AES for the former. Options for an AES-based round function include
4
剩余17页未读,继续阅读
资源评论

nfgo
- 粉丝: 766
- 资源: 80
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- 基于springboot+vue的图书进销存管理系统(Java毕业设计,附源码,部署教程).zip
- 数据结构 课程设计报告 线性表运算器
- 基于springboot+vue的秒杀系统设计与实现(Java毕业设计,附源码,部署教程).zip
- 基于springboot+vue的美食推荐商城的设计与实现(Java毕业设计,附源码,部署教程).zip
- 基于springboot+vue的网上订餐系统(Java毕业设计,附源码,部署教程).zip
- 基于springboot+vue的网上购物商城系统研发(Java毕业设计,附源码,部署教程).zip
- 基于springboot+vue的网上点餐系统(Java毕业设计,附源码,部署教程).zip
- 基于springboot+vue的林业产品推荐系统(Java毕业设计,附源码,部署教程).zip
- 基于springboot+vue的网上租赁系统设计与实现(Java毕业设计,附源码,部署教程).zip
- 基于springboot+vue的蜗牛兼职网的设计与实现(Java毕业设计,附源码,部署教程).zip
- 基于springboot+vue的网页时装购物系统(Java毕业设计,附源码,部署教程).zip
- 基于springboot+vue的企业资产管理系统(Java毕业设计,附源码,部署教程).zip
- 基于springboot+vue的企业级工位管理系统(Java毕业设计,附源码,部署教程).zip
- 基于springboot+vue的企业oa管理系统(Java毕业设计,附源码,部署教程).zip
- 基于springboot+vue的校园管理系统的设计与实现(Java毕业设计,附源码,部署教程).zip
- 基于springboot+vue的人力资源管理系统的设计与实现(Java毕业设计,附源码,部署教程).zip
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功