没有合适的资源?快使用搜索试试~ 我知道了~
COMSOL Multiphysics:流体流动模块理论与实践.Tex.header.docx
1.该资源内容由用户上传,如若侵权请联系客服进行举报
2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
版权申诉
0 下载量 176 浏览量
2024-08-24
11:27:49
上传
评论
收藏 30KB DOCX 举报
温馨提示
工业软件系列教程。
资源推荐
资源详情
资源评论

1
COMSOL Multiphysics:流体流动模块理论与实践
1 COMSOL Multiphysics: 流体流动模块理论与实践
1.1 简介
1.1.1 COMSOL Multiphysics 概述
COMSOL Multiphysics 是一款强大的多物理场仿真软件,它允许用户在单一
环境中模拟和分析多种物理现象,包括流体流动、传热、结构力学、电磁学等。
通过其直观的用户界面和灵活的建模功能,COMSOL Multiphysics 为科研人员、
工程师和学生提供了一个全面的工具,用于解决复杂的工程问题和科学研究。
1.1.2 流体流动模块的功能与应用
流体流动模块是 COMSOL Multiphysics 的一个重要组成部分,专门用于模拟
流体在各种条件下的行为。该模块基于 Navier-Stokes 方程,能够处理层流、湍
流、多相流、微流体和气体动力学等问题。它还提供了与传热、化学反应、声
学等其他物理场耦合的能力,使得用户可以模拟流体流动与这些现象的相互作
用。
流体流动模块的应用范围广泛,包括但不限于:
� 航空航天:模拟飞机机翼周围的气流,优化设计以减少阻力和提
高效率。
� 汽车工业:分析发动机冷却系统,确保发动机在各种条件下都能
有效散热。
� 生物医学工程:研究血液流动,设计更有效的医疗设备,如人工
心脏瓣膜。
� 环境科学:模拟污染物在水体或大气中的扩散,评估环境影响。
� 化学工程:优化反应器设计,确保反应物的均匀混合和高效反应。
1.2 理论基础
1.2.1 Navier-Stokes 方程
流体流动模块的核心是 Navier-Stokes 方程,这是一组描述流体动力学的偏
微分方程。在不可压缩流体的情况下,方程可以简化为:
ρ
∂
u
∂
t
+
u
⋅
∇
u
=
−
∇
p
+
μ
∇
2
u
+
f
其中,
ρ
是流体的密度,
u
是流体的速度向量,
p
是压力,
μ
是动力粘度,
f
是
外部力向量。

2
1.2.2 湍流模型
对于高速流动或大尺度流动,流体流动模块提供了多种湍流模型,如 k-ε
模型和 k-ω模型。这些模型通过引入额外的方程来描述湍流的统计特性,从而
更准确地模拟流体的非线性行为。
1.3 实践操作
1.3.1 建立流体流动模型
在 COMSOL Multiphysics 中建立流体流动模型,首先需要选择合适的物理场
接口。例如,对于层流,可以选择“层流”接口;对于湍流,可以选择“湍流”
接口。接下来,定义几何形状、网格、边界条件和初始条件。
1.3.1.1 示例:层流管道流动
假设我们要模拟一个简单管道内的层流流动,管道直径为 0.01 米,长度为
1 米,流体为水,入口速度为 0.1 米/秒。
1. 选择物理场接口:在 COMSOL 中选择“层流”接口。
2. 定义几何形状:创建一个圆柱形管道。
3. 网格划分:使用“自由网格”生成网格。
4. 边界条件:设置入口速度为 0.1 米/秒,出口为压力出口,管道壁
面为无滑移边界。
5. 求解:设置求解器参数,运行仿真。
1.3.1.2 代码示例
在 COMSOL 中,虽然主要通过图形界面操作,但也可以使用 MUMPS 求解
器进行更高级的控制。以下是一个使用 MUMPS 求解器的代码示例:
%
设置
MUMPS
求解器参数
mumpsSolver = mphselect("mumps");
mumpsSolver.Method = "Direct";
mumpsSolver.Prec = "None";
mumpsSolver.MaxIter = 1000;
mumpsSolver.AbsTol = 1e-6;
mumpsSolver.RelTol = 1e-4;
%
应用求解器设置
mphset(mumpsSolver, "Model");
%
运行仿真
mphrun("Model");

3
1.3.2 后处理与结果分析
完成仿真后,COMSOL 提供了丰富的后处理工具,用于可视化和分析结果。
用户可以创建各种类型的图表和动画,如流线图、压力分布图、速度矢量图等,
以直观地理解流体流动的特性。
1.3.2.1 示例:分析管道流动结果
在上述管道流动模型中,我们可以分析流体的速度分布、压力分布和流线
图,以了解流体在管道内的行为。
1. 速度分布:创建一个切面图,显示管道中心线的速度分布。
2. 压力分布:生成一个管道壁面的压力分布图。
3. 流线图:在管道内创建流线图,观察流体的流动路径。
1.4 结论
通过 COMSOL Multiphysics 的流体流动模块,用户可以深入理解流体在各种
条件下的行为,从而优化设计、提高效率和解决复杂问题。无论是层流还是湍
流,无论是单相流还是多相流,COMSOL 都能提供强大的工具和算法,帮助用
户进行精确的仿真和分析。
请注意,上述代码示例和操作步骤是基于 COMSOL 的 MATLAB 接口,实际
操作可能需要根据具体版本和界面进行调整。此外,流体流动模块的深入应用
和理论理解需要结合具体工程问题和物理背景,进行细致的分析和设计。
2 流体流动基础理论
2.1 流体动力学基本方程
流体动力学是研究流体(液体和气体)在静止和运动状态下的行为。在
COMSOL Multiphysics 中,流体流动模块基于连续介质假设,使用纳维-斯托克斯
方程(Navier-Stokes equations)来描述流体的运动。这些方程是流体动力学的
核心,它们描述了流体的动量、质量和能量守恒。
2.1.1 质量守恒方程(连续性方程)
质量守恒方程描述了流体质量在任意体积内的守恒。在不可压缩流体中,
该方程简化为:
∇
⋅
u
=
0
其中,
u
是流体的速度向量。
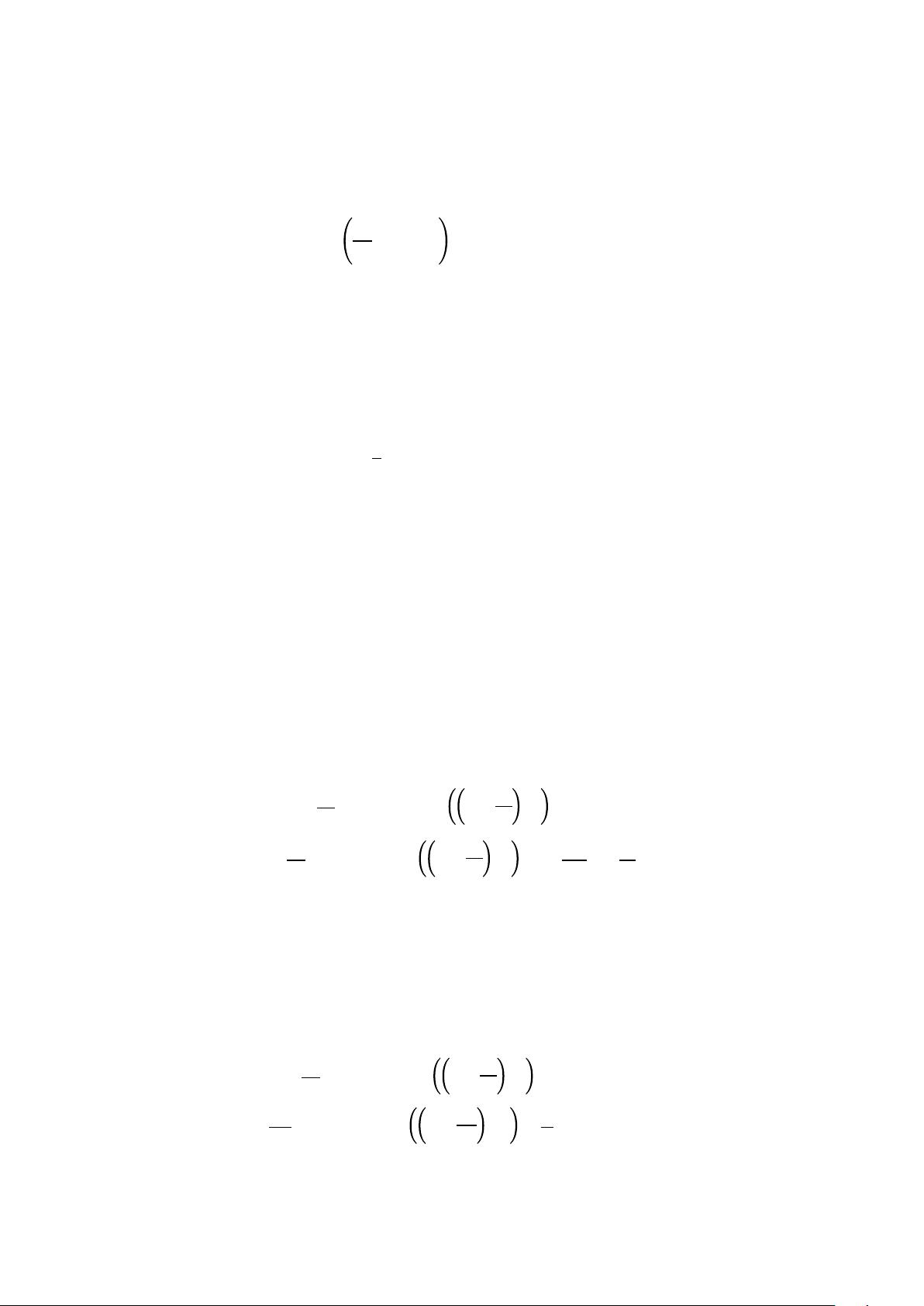
4
2.1.2 动量守恒方程(纳维-斯托克斯方程)
动量守恒方程描述了作用在流体上的力与流体动量变化之间的关系。对于
不可压缩流体,无粘性流体的纳维-斯托克斯方程可以表示为:
ρ
∂
u
∂
t
+
u
⋅
∇
u
=
−
∇
p
+
μ
∇
2
u
+
f
其中,
ρ
是流体的密度,
p
是流体的压力,
μ
是流体的动力粘度,
f
是作用在
流体上的体积力。
2.1.3 能量守恒方程
能量守恒方程描述了流体内部能量的变化,包括热能和动能。在稳态、无
粘性流体中,能量守恒方程简化为伯努利方程:
1
2
ρ
u
2
+
p
+
ρ
g
z
=
常数
其中,
u
是流体的速度,
g
是重力加速度,
z
是垂直高度。
2.2 湍流模型介绍
在实际应用中,流体流动往往不是层流,而是湍流。湍流模型用于描述这
种复杂流动,COMSOL 提供了多种湍流模型,包括 k-ε模型、k-ω模型和雷诺
应力模型。
2.2.1 k-ε 模型
k-ε模型是最常用的湍流模型之一,它基于湍流能量
k
和湍流耗散率
ε
的传
输方程。在 COMSOL 中,k-ε模型的方程组可以表示为:
∂
k
∂
t
+
u
⋅
∇
k
=
∇
⋅
ν
+
ν
t
σ
k
∇
k
+
P
k
−
ε
∂
ε
∂
t
+
u
⋅
∇
ε
=
∇
⋅
ν
+
ν
t
σ
ε
∇
ε
+
C
1
P
k
ε
k
−
C
2
ε
2
k
其中,
ν
是流体的动力粘度,
ν
t
是湍流粘度,
σ
k
和
σ
ε
是湍流 Prandtl 数,
P
k
是
湍流能量的产生项。
2.2.2 k-ω 模型
k-ω模型使用湍流能量
k
和湍流频率
ω
来描述湍流。在 COMSOL 中,k-ω模
型的方程组可以表示为:
∂
k
∂
t
+
u
⋅
∇
k
=
∇
⋅
ν
+
ν
t
σ
k
∇
k
+
P
k
−
β
∗
ω
k
∂
ω
∂
t
+
u
⋅
∇
ω
=
∇
⋅
ν
+
ν
t
σ
ω
∇
ω
+
ω
k
(
C
1
P
k
−
C
2
ω
k
)
其中,
β
∗
、
σ
k
、
σ
ω
、
C
1
和
C
2
是模型常数。
剩余16页未读,继续阅读
资源评论


kkchenjj
- 粉丝: 2w+
- 资源: 5479
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功

