没有合适的资源?快使用搜索试试~ 我知道了~
材料力学之动力学分析算法:模态分析:材料力学基础理论.Tex.header.docx
1.该资源内容由用户上传,如若侵权请联系客服进行举报
2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
版权申诉
0 下载量 46 浏览量
2024-08-23
13:54:50
上传
评论
收藏 33KB DOCX 举报
温馨提示
材料力学之动力学分析算法:模态分析:材料力学基础理论.Tex.header.docx
资源推荐
资源详情
资源评论

1
材料力学之动力学分析算法:模态分析:材料力学基础理
论
1 绪论
1.1 模态分析在工程中的应用
模态分析是工程领域中一种重要的动力学分析方法,广泛应用于结构动力
学、振动控制、声学分析、故障诊断等多个领域。通过模态分析,工程师可以
识别结构的固有频率、阻尼比和振型,这些信息对于设计和优化结构至关重要。
例如,在航空航天工业中,模态分析用于预测飞机在飞行过程中的振动特性,
确保其在各种飞行条件下的稳定性和安全性。在汽车工业中,模态分析帮助设
计者减少车辆的噪音、振动和不平顺性,提升乘坐舒适度。
1.2 模态分析的基本概念
模态分析的核心概念包括固有频率、振型和阻尼比。固有频率是结构在自
由振动时的振动频率,反映了结构的固有动力学特性。振型描述了结构在特定
固有频率下振动的形状,即结构各部分的相对位移。阻尼比则衡量了结构振动
能量的衰减程度,影响振动的持续时间和振幅。
1.2.1 固有频率
固有频率是结构在无外力作用下自由振动的频率,通常用赫兹(Hz)表示。
对于一个具有多个自由度的系统,存在多个固有频率,每个频率对应一个振型。
1.2.2 振型
振型是结构在特定固有频率下振动的模式,表示结构各部分的相对位移。
振型可以可视化,帮助工程师理解结构在振动时的变形情况。
1.2.3 阻尼比
阻尼比是衡量结构振动能量衰减程度的参数,通常定义为实际阻尼与临界
阻尼的比值。阻尼比影响结构振动的持续时间和振幅,对于预测结构在实际环
境中的动力学行为至关重要。
1.3 示例:模态分析的 MATLAB 实现
下面通过一个简单的例子来展示如何使用 MATLAB 进行模态分析。假设我
们有一个具有两个自由度的线性系统,其质量矩阵
M
和刚度矩阵
K
如下:
2
%
定义质量矩阵
M
和刚度矩阵
K
M = [1, 0; 0, 1]; %
单位质量
K = [2, -1; -1, 2]; %
单位刚度
1.3.1 步骤 1:计算固有频率和振型
使用 MATLAB 的 eig 函数来计算系统的固有频率和振型。
%
计算固有频率和振型
[V, D] = eig(K, M);
omega = sqrt(diag(D)); %
固有频率的平方根
phi = V; %
振型
1.3.2 步骤 2:可视化振型
使用 MATLAB 的绘图功能来可视化振型。
%
可视化振型
figure;
plot(phi(1,:), phi(2,:), 'o-');
xlabel('自由度 1');
ylabel('自由度 2');
title('振型可视化');
1.3.3 步骤 3:分析阻尼比
假设系统具有比例阻尼,即阻尼矩阵
C
可以表示为质量矩阵
M
和刚度矩阵
K
的线性组合。
%
定义阻尼矩阵
C
alpha = 0.1; %
质量比例阻尼系数
beta = 0.05; %
刚度比例阻尼系数
C = alpha*M + beta*K; %
阻尼矩阵
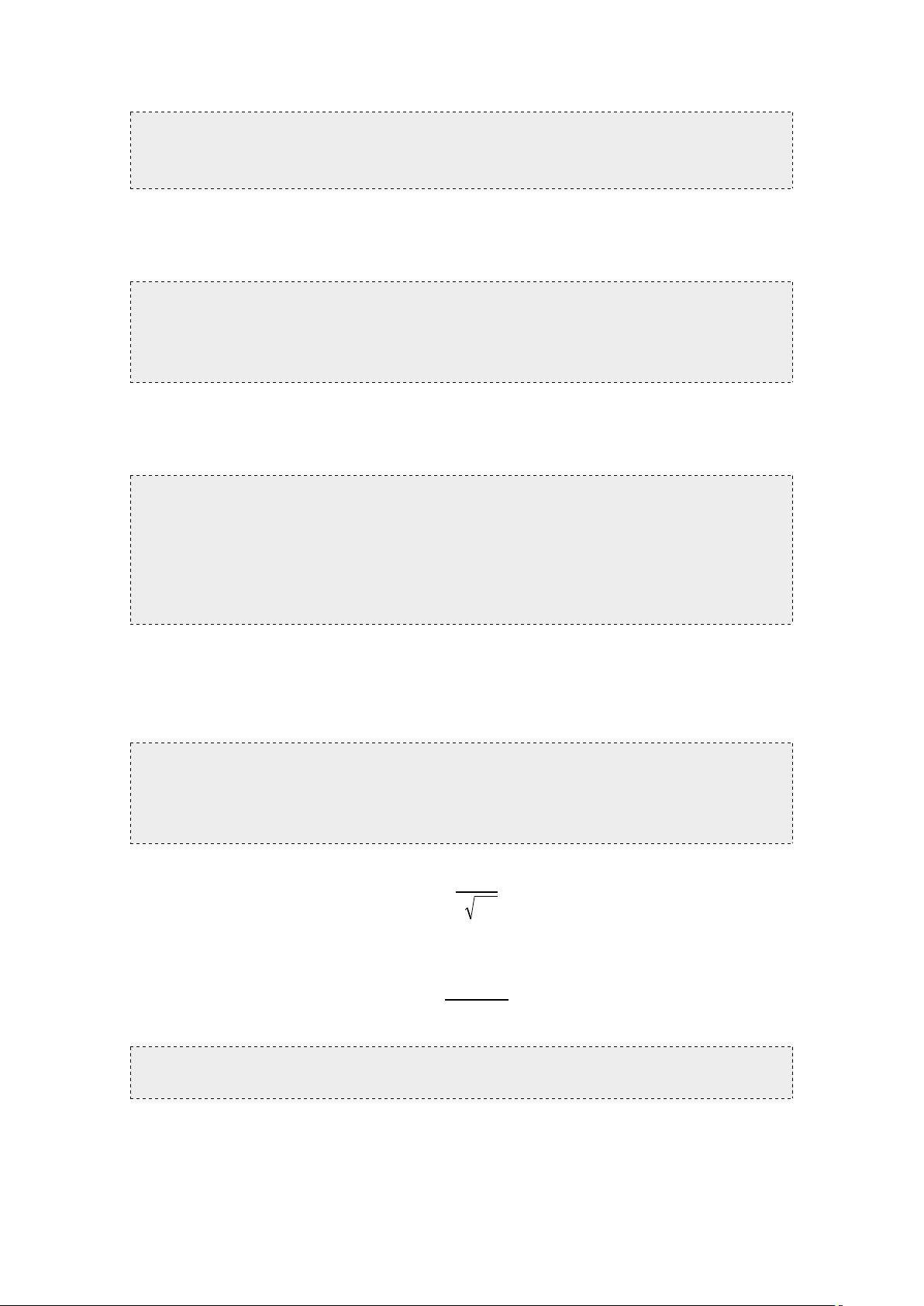
阻尼比可以通过下面的公式计算:
ξ
=
c
2
m
k
其中
c
是阻尼系数,
m
是质量,
k
是刚度。对于比例阻尼,阻尼比可以简化
为:
ξ
=
α
+
β
ω
2
2
ω
其中
ω
是固有频率。
%
计算阻尼比
xi = (alpha + beta*omega.^2) / (2*omega);
1.3.4 步骤 4:结果解释
通过计算得到的固有频率、振型和阻尼比,工程师可以分析结构的动力学

3
特性。固有频率揭示了结构的自然振动频率,振型展示了结构在这些频率下的
振动模式,而阻尼比则提供了结构振动能量衰减的信息。
1.4 结论
模态分析是材料力学和结构工程中不可或缺的工具,它帮助工程师理解和
预测结构在动力学环境下的行为。通过 MATLAB 等工具,模态分析可以高效地
进行,为结构设计和优化提供关键数据。
2 材料力学基础
2.1 应力与应变的定义
2.1.1 应力
应力(Stress)是材料力学中的基本概念,定义为单位面积上的内力。在材
料力学中,应力可以分为正应力(Normal Stress)和切应力(Shear Stress)。正
应力是垂直于截面的应力,而切应力则是平行于截面的应力。应力的单位通常
为帕斯卡(Pa),即牛顿每平方米(N/m²)。
2.1.2 应变
应变(Strain)是材料在受力作用下发生的形变程度的量度。应变没有单位,
因为它是一个无量纲的比值。应变可以分为线应变(Linear Strain)和剪应变
(Shear Strain)。线应变是材料在某一方向上的长度变化与原长度的比值,而剪
应变则是材料在剪切力作用下发生的角形变。
2.2 材料的弹性与塑性行为
2.2.1 弹性行为
材料在弹性范围内,其应力与应变之间遵循胡克定律(Hooke’s Law),即
应力与应变成正比关系。弹性模量(Elastic Modulus)是描述材料弹性行为的重
要参数,包括杨氏模量(Young’s Modulus)、剪切模量(Shear Modulus)和体
积模量(Bulk Modulus)。
2.2.2 塑性行为
当材料受到的应力超过其弹性极限时,材料会发生永久形变,即塑性形变。
塑性行为通常用屈服强度(Yield Strength)和极限强度(Ultimate Strength)来
描述。屈服强度是材料开始发生塑性形变时的应力值,而极限强度是材料在断
裂前能承受的最大应力值。

4
2.3 材料力学中的能量原理
2.3.1 能量原理概述
材料力学中的能量原理是基于能量守恒的概念,用于分析和解决材料在受
力作用下的变形和稳定性问题。能量原理包括最小势能原理(Principle of
Minimum Potential Energy)和最小总势能原理(Principle of Minimum Total
Potential Energy)。
2.3.2 最小势能原理
最小势能原理指出,在静力平衡条件下,当外力做功与内能变化相等时,
系统处于稳定状态。这一原理常用于求解弹性体的平衡问题。
2.3.3 最小总势能原理
最小总势能原理是考虑了外力做功、内能变化以及动能变化的综合能量原
理。在动力学分析中,这一原理尤为重要,因为它可以用于分析材料在动态载
荷作用下的响应。
2.3.4 示例:使用 Python 计算弹性体的应变能
#
导入必要的库
import numpy as np
#
定义材料参数
E = 200e9 #
杨氏模量,单位:
Pa
nu = 0.3 #
泊松比
#
定义应变矩阵
epsilon = np.array([[0.001, 0.0005, 0.0],
[0.0005, 0.002, 0.0],
[0.0, 0.0, 0.0]])
#
计算应力矩阵,使用胡克定律
stress = E / (1 - nu**2) * (epsilon + nu * np.transpose(epsilon) - (nu/(1-2*nu)) * np.trace(epsilon)
* np.eye(3))
#
计算应变能密度
strain_energy_density = 0.5 * np.sum(stress * epsilon)
#
输出结果
print(f"应变能密度为:{strain_energy_density} J/m³")
剩余19页未读,继续阅读
资源评论


kkchenjj
- 粉丝: 2w+
- 资源: 5499
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- 现场评定检查表——建筑外墙、屋面保温和建筑外墙装饰.docx
- 现场评定检查表--气体灭火系统.docx
- 消防第三方技术服务模拟验收抽查记录表.doc
- 现场评定检查表——总平面布局.docx
- 消防验收过程服务--现场记录表.doc
- 消防第三方技术服务现场交底监督记录表.doc
- 向日葵被控端绿色精简运行版
- 学生心理档案表.docx
- 验收确认单表格.docx
- 阳宅净宅表文.docx
- 医疗废弃物建设项目环境风险简单分析表.docx
- 原材料检测报告.docx
- 造林补助实施方案小班一览表、造林补助(新增部分)分行政村(国有林场)任务落实情况表.xls
- 造林补助(新增部分)分行政村(国有林场)任务落实情况表.docx
- 肢体残疾标准.docx
- 职工工伤与职业病致残等级分级表十级.docx
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功