ERD_滑动窗口_信号检测_突发通信_突发检测_非合作信号

共2个文件

pdf：1个

m：1个

版权申诉

滑动窗口

信号检测

突发通信

5星 · 超过95%的资源 147 浏览量 2021-09-11 05:58:07 上传评论 6 收藏 2.94MB ZIP 举报

在无线通信领域，突发通信（Burst Communication）是一种常见的数据传输方式，特别是在非合作通信环境中，比如无人监控的传感器网络或者敌对环境下的军事通信。在这种场景下，发送方可能不希望被轻易检测到，因此信号通常是短暂且不规则的，被称为“突发信号”。本文将重点探讨一种用于检测此类信号的技术——滑动窗口能量比值法（Energy Ratio Detector, ERD），并结合提供的ERD.m代码和non-cooperative burst detection.pdf论文来深入理解这一方法。滑动窗口（Sliding Window）是信号处理中的一种常见技术，它通过在连续的数据序列上移动一个固定长度的窗口，以分析窗口内数据的特性。在信号检测中，滑动窗口可以帮助我们捕获短时间内信号的变化，这对于识别突发通信中的信号起始和结束位置至关重要。 ERD算法的核心思想是利用信号能量的比值来判断是否存在突发信号。具体来说，算法会计算当前窗口和前一窗口内的信号能量，然后比较这两个能量的比值。当比值超过预设阈值时，我们可以认为检测到了一个信号的开始或结束。这是因为突发信号通常会在短时间内产生显著的能量变化，而背景噪声则相对稳定。因此，能量比值的变化可以作为检测信号活动的有效指标。在ERD.m代码中，我们可以看到以下步骤： 1. 初始化滑动窗口大小、阈值等参数。 2. 对输入信号进行分帧，每帧对应一个滑动窗口。 3. 计算相邻两帧的信号能量比值。 4. 比较比值与设定阈值，判断是否满足信号开始或结束的条件。 5. 输出检测结果，包括信号起始和结束的位置。论文"non-cooperative burst detection.pdf"应该详细阐述了ERD的理论基础，包括数学模型、性能分析以及实际应用中的优化策略。它可能还讨论了如何选择合适的窗口大小和阈值，以平衡检测性能和假警报率。此外，论文可能还会探讨ERD与其他信号检测方法的比较，以及在不同信噪比和信号特征下的表现。滑动窗口能量比值法ERD是一种针对非合作纯盲突发信号的检测技术，它通过分析信号能量的局部变化来识别信号的存在。结合ERD.m代码和论文，我们可以更深入地理解这一方法，并将其应用于实际的通信系统中，以提高信号检测的准确性和效率。

资源推荐

资源详情

资源评论

收起资源包目录

ERD_滑动窗口_信号检测_突发通信_突发检测_非合作信号_源码.zip （2个子文件）

non-cooperative burst detection.pdf 3.05MB

ERD.m 5KB

IET Communications

Research Article

Non-cooperative burst detection and

synchronisation in downlink TDMA-based

wireless communication networks

ISSN 1751-8628

Received on 15th June 2018

Revised 21st November 2018

Accepted on 16th January 2019

E-First on 18th March 2019

doi: 10.1049/iet-com.2018.5536

www.ietdl.org

Maryam Zebarjadi

, Mehdi Teimouri

Information Theory and Coding Laboratory, Faculty of New Sciences and Technologies, University of Tehran, Iran

E-mail: mehditeimouri@ut.ac.ir

Abstract: Blind signal detection is very important in various applications such as cognitive radio, spectrum surveillance, and

eavesdropping. This gets trickier when one needs to deal with burst signals (as opposed to continuously transmitted signals) in

non-cooperative environments. Here, existing methods for signal detection are studied and developed to use for burst detection.

For the special case of downlink time division multiple access (TDMA) burst transmission, performances of these detection

methods are improved by proposing a blind synchronisation algorithm which is applied to the output result of detection

algorithms. The results of Monte–Carlo simulations demonstrate the performance of the proposed detection and synchronisation

algorithms.

1 Introduction

Blind signal identification is an important research topic in modern

telecommunication technology. Nowadays, non-cooperative signal

processing is one of the essential necessities in the design of

intelligent receivers [1]. Blind signal detection, blind modulation

recognition, and blind channel code reconstruction are three

fundamental steps in non-cooperative receivers [2]. Signal

detection is the first step in such receivers. All the subsequent steps

rely on the results of signal detection phase, so an intelligent

receiver must be equipped with an accurate signal detector.

Various signal detection methods have been proposed and

utilised in different applications. In spectrum sensing technology,

various sensing methods are proposed [3]. Energy Detector (ED) is

the simplest and the most popular algorithm. In this method, the

receiver measures the received signal energy and compares it with

a threshold that depends on the noise level [4–12]. ED method does

not need to know any information about the signal and the fading

channel. However, this method needs to estimate the noise level.

As a result, a small error in the estimation of noise level affects the

detection result. Methods based on covariance matrix and

eigenvalues are proposed for resolving this issue. Signal detection

based on the eigenvalues of covariance matrix is investigated by

various papers [3, 13–16]. In [17], maximum eigenvalue detector

(MED) is proposed. The authors of [18] have suggested the ratio of

the maximum eigenvalue to the minimum eigenvalue detector.

Cyclostationary features are also proposed for signal detection [19,

20]. However, when the noise is stationary, ED methods

outperforms cyclostationary-based methods [21]. Matched filtering

detector (MFD) is also considered for signal detection in [22, 23].

MFD has higher accuracy in low signal-to-noise ratio (SNR)

conditions, and it is more robust to noise-level uncertainty.

However, MFD needs specific knowledge about the transmitted

waveform patterns which is the drawback of the method in blind

situations. For comprehensive comparisons between various signal

detection methods, the reader is referred to [21, 24].

In all the above-mentioned methods, signal-detection process is

modelled as a binary hypothesis testing. The null hypothesis is the

situation in which only noise is present and the alternative

hypothesis is the situation in which signal is received in a noisy

environment. This hypothesis testing is suited for environments in

which continuous signal is transmitted. Signal detection gets more

complicated when one needs to deal with burst signals (as opposed

to continuously transmitted signals). In this situation, signal

detection is not accomplished only by checking the presence or

absence of the signal. In this case, it is also necessary to determine

the exact position of bursts.

In communications based on burst signals, different users

transmit their burst information by using a radio channel and each

burst conveys a data packet to a particular receiver. In order to

prevent the interference between adjacent bursts, a guard time is

usually considered between them. In a non-cooperative

environment, the position of the bursts and the guard times must be

exactly determined by the receiver without any prior knowledge

about signal. So, we can define blind detection of burst signals as

determination of the beginning and ending time of all bursts. Since

the received signal may contain bursts with different lengths, an

efficient detector should have the ability to detect bursts of

different lengths. It also should detect very short guard times.

Transient signal detection is a concept which is very relevant to

burst detection. Transient signal detection arises in applications

such as telemetry and spread spectrum communications. Transient

signals are generally considered as short duration signals compared

to the observation time. The aim of transient signal detector is to

decide whether the observation consists of noise alone or the signal

is embedded in noise [25–27]. Various detection schemes have

been proposed for this purpose. Selecting an appropriate detection

method depends on the amount of knowledge that is available to

the detector. Such knowledge includes the arrival time of transient

signal, the duration of the transient signal, and the waveform shape

of the signal. For instance, matched filtering is the optimal method

if the transient signal is known. When the transient signal is

partially known, an often used procedure is the likelihood ratio test

(LRT). When the signal to be detected is unknown, energy-based

detectors become the only choice [25]. In [26], the performance of

transient detection based on higher order moments is investigated

and a detector based on the third-order absolute moment is

proposed. Order statistics (OS)-based signal processing is also

applied to transient detection, and it is shown that the duration of

an unknown transient signal can be estimated by use of OS

technique [27]. In [28], a method based on permutation entropy is

introduced for recognition of starting time of a transient signal.

GSM signal is used for evaluating the performance of this

detection technique where each time slot is considered as a

transient signal. Since there is no information available about the

frame structure and time slots in a non-cooperative environment,

the above-mentioned methods for transient signal detection are not

applicable. Moreover, existence of multiple bursts with different

lengths is not considered in transient signal-detection formulation.

IET Commun., 2019, Vol. 13 Iss. 7, pp. 863-872

863

Authorized licensed use limited to: BEIJING INSTITUTE OF TECHNOLOGY. Downloaded on September 02,2020 at 05:32:37 UTC from IEEE Xplore. Restrictions apply.

Here, transient signal detection model is generalised and solved for

the problem of burst signal detection.

In wireless telecommunication networks, burst transmission is

usually employed in two different scenarios: first when a

contention-based channel access is used in the network (e.g. in

IEEE 802.11 [29]) and second when a time division multiple

access (TDMA) scheme is implemented (e.g. in GSM standard

[30]). Many researches have been done on design of a receiver for

TDMA signals in a cooperative environment. For example, the

structure of receiver in satellite telecommunications is investigated

in [31]; frame and burst acquisition in TDMA satellite

communication networks via unique word pattern is considered in

[32]; data detection for burst mode signal via polynomial

interpolation is proposed in [33]. In [34], energy ratio detector

(ERD) is employed for recognition of bursts. However, like all the

other methods, it is assumed that the structure of the received

signal is known to the receiver.

We define burst detection as a problem in which the aim is to

find the start and the end of all bursts (i.e. data packets) in an

eavesdropped signal. In other words, burst detection can be seen as

a generalised transient detection problem where there is more than

one transient in the received signal. Besides, the lengths of

transients are assumed to be unknown. Despite the importance of

this problem, to the best of authors' knowledge, no solid published

research is available for blind burst detection in non-cooperative

environments. In burst detection context, there are only some

rudimentary published researches. For example, in [35],

fluctuations of autocorrelation function are used to detect burst

signals. The idea is that the autocorrelation function has higher

values when the received signal includes burst compared to when

only noise is present. However, neither Monte–Carlo simulations

nor any performance criterion are presented.

Here, autocorrelation detector (ACD), ED, ERD, and maximum

to minimum eigenvalue detector (MMED) are modified and

generalised for solving the problem of burst detection. The

performance of these methods is measured in different scenarios

via Monte–Carlo simulation. Despite the acceptable accuracy of

the detectors, for the special case of downlink TDMA burst

transmission, the performance of detection methods is improved by

proposing a blind synchronisation algorithm based on the

regularity of the bursts in downlink TDMA structure. The proposed

synchronisation algorithm is an iterative algorithm which is applied

on the initial detection. The results of simulations demonstrate that

the synchronisation algorithm can improve the results of initial

detection of ED, MMED, ACD, and ERD. It should be noted again

that the problem investigated here is different from the cooperative

(i.e. non-blind) TDMA synchronisation in which the TDMA

structure and synchronisation patterns are known to the receiver

[31–33, 36–38]. In fact, in cooperative communications, some

additional bits or specific patterns are generally embedded in the

bursts to help the authorised receiver for synchronisation.

The rest of this paper is organised as follows. In Section 2,

signal model is presented. In Sections 3, ACD, ED, ERD, and

MMED are generalised and developed for burst detection. In

Section 4, a blind synchronisation algorithm is proposed for

downlink TDMA signals based on the regularity of bursts in

downlink TDMA structure. Simulation results are presented in

Section5. Finally, the paper is concluded in Section 6.

2 Signal model

Consider a wireless communication network which employs a

burst-mode data transmission scheme. In such network, each user

transmits its packets by means of some bursts. The bursts are

distributed according to either a predefined rule (e.g. TDMA) or a

contention-based channel access method. Assume that the received

(i.e. eavesdropped) signal is sampled at a specific sampling rate.

So, in burst i, n

(i) noisy signal samples are received. Usually, a

guard time is considered after each burst in order to prevent

transmitted bursts from different users overlapping due to different

path delays. Assume that the length of guard for burst i is n

(i)

samples. Also, assume that N

samples are received (i.e.

eavesdropped) and there exist M

bursts in these observations (M

depends on N

). So, the received signal samples can be modelled as

r( j) =

s(j) + n(j) for

∑

i = 1

(i) samples

n(j) for N

−

∑

i = 1

(i) samples

(1)

where n( j) ( j = 1, 2, . . . , N

) are samples of independent complex

additive Gaussian noise with known variance σ

per real

dimension. Moreover, the values of s(j) ( j = 1, 2, . . . , N

) are the

samples of received bursts. Note that, in this model which is the

generalised form of the model proposed in [26] for transient signal

detection, bursts samples are aggregated into a single stream s(j). If

= 1 and the samples of n

(1) are considered to be consecutively

transmitted, transient signal model is obtained.

In both predefined and contention-based channel access

methods, the number of transmitted bursts may be less than the

maximum available bursts. For example, in TDMA channel access

method, a user may or may not have a packet to send in its pre-

allocated time slots. For TDMA, we define channel occupancy rate

(COR) as follows

COR =

lim

→ ∞

∑

i = 1

(i) + n

(i)

(2)

Usually, in TDMA channel access method, the length of all bursts

(and likewise the length of all guards) are assumed to be equal. In

other words,

(i) = n

and

(i) = n

for

i = 1, 2, . . . , M

The aim of the blind receiver is to obtain the values of

(i); i = 1, 2, …, M

and the exact position of the bursts in the

received samples

r( j); j = 1, 2, …, N

. In other words, a blind

receiver should estimate the start and the end of all bursts (i.e. data

packets) in an eavesdropped signal. By using a binary function

(denoted by

(j); j = 1, 2, …, N

), the position of bursts can be

defined as follows: for the samples corresponding to the bursts, the

value of w

(j) is 1; and for the samples corresponding to the guard

times (i.e. noise-only samples), the value of

(j) is 0. If we define

dummy signal samples corresponding to

− ∑

i = 1

(i)

noise-

only samples in (1), we can rewrite (1) as

r( j) = w

(j)s(j) + n( j); j = 1, 2, . . . , N

(3)

where

(j) =

1 for

∑

i = 1

(i) burst samples

0 for N

−

∑

i = 1

(i) noise − only samples

(4)

We call

(j) the reference burst position indicator. Let us denote

the estimation of the blind receiver about

(j) by

(j). In ideal

receiver,

(j) = w

(j) for

j = 1, 2, . . . , N

. However, in practical

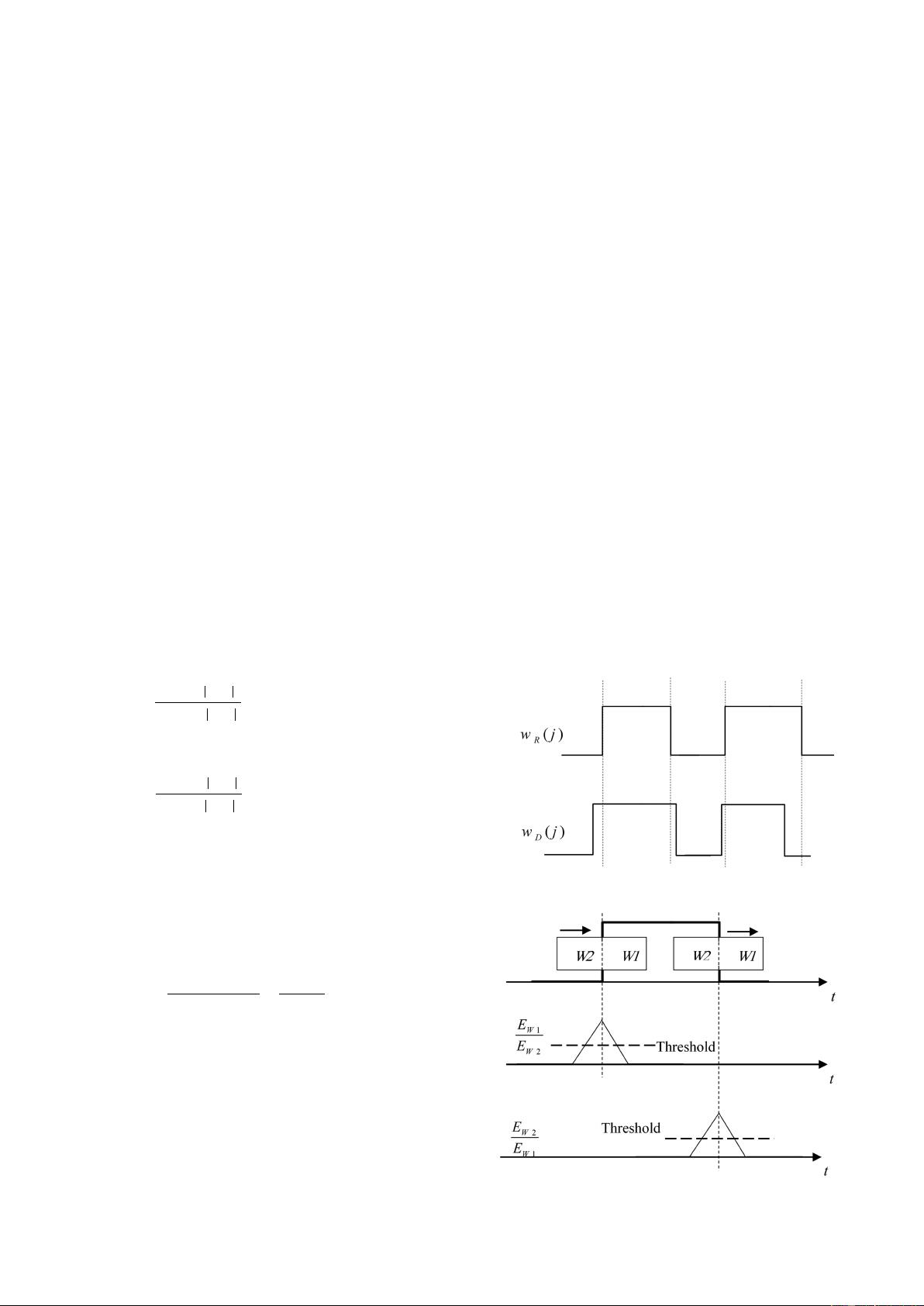
situations,

(j) and

(j) may not be identical functions (see

Fig. 1). We propose to use Dice similarity coefficient [39] for

evaluating the accuracy of the blind burst detector. Since w

(j) and

(j) are binary functions, we can write Dice similarity coefficient

between w

(j) and

(j) as

D(w

, w

) =

∑

j = 1

1 − w

(j) 1 − w

(j)

∑

j = 0

− 1

(j)w

(j)

(5)

It is obvious that in the case of error-free estimation, we have

D(w

, w

) = 1

. We can express Dice similarity coefficient in

percentage if we multiply both sides of (5) by 100.

864 IET Commun., 2019, Vol. 13 Iss. 7, pp. 863-872

Authorized licensed use limited to: BEIJING INSTITUTE OF TECHNOLOGY. Downloaded on September 02,2020 at 05:32:37 UTC from IEEE Xplore. Restrictions apply.

Although Dice similarity coefficient is a good criterion for

evaluating the accuracy of the detector, it is not sufficient. For

example, consider a burst signal with very short guard times. If the

detector cannot detect the guards in this case, the value of Dice

similarity coefficient is still high due to the large number of bursts

samples in the signal. So, we employ two other metrics here: error

in burst detection and error in guard detection. The error in burst

detection, which is denoted by E

and it is simply called burst

error, is obtained by dividing the number of burst samples

identified as noise-only samples by the total number of burst

samples. Similarly, the error in guard detection, which is denoted

it is simply called guard error, is obtained by dividing the

number of guard samples identified as burst samples by the total

number of guard samples.

3 Burst detection methods

As mentioned earlier, there are many well-known methods for

detecting the presence of signal. In this section, four approaches

ERD, ED, MMED, and ACD are generalised and developed for

burst detection problem.

3.1 Energy ration detector (ERD)

ERD utilises the changes in the energy ratio of two adjacent time

windows in order to find the burst position function (i.e. w

(j)).

Let us consider two adjacent windows W1 and W2 with the same

length L and slide them along the received signal. Since in the

beginning and in the end of the bursts, the energy of the signal

changes more intensely, we expect that the ratio of the energies in

W1 and W2 take very small or very large values at these boundary

points (see Fig. 2).

The energy ratio of the first window to the second window is

very large when the first window is located entirely in the burst and

the second window is placed completely in the guard. On the other

hand, at the end of the bursts, this ratio is very small. So, we can

employ inverse of this ratio for finding the ending times.

In fact, the ratios

(k) =

∑

m = k

k + L − 1

r(m)

∑

m = k − L

k − 1

r(m)

, k = L + 1, . . . N

− L + 1

(6)

and

(k) =

∑

m = k − L

k − 1

r(m)

∑

m = k

k + L − 1

r(m)

, k = L + 1, . . . N

− L + 1

(7)

are used for locating the start and the end points of bursts,

respectively. As it can be seen in Fig. 2, a threshold must be

defined in order to locate bursts. Assume that the power of the

received signal samples in burst durations is constant and equal to

. Moreover, according to (1), the power of noise samples is equal

= 2σ

. So, in the start and in the end points of the bursts, the

ratio of energies in the adjacent windows are approximately equal

AER

max

≃

× L + P

× L

+ P

= 1 + SNR,

(8)

where SNR is the signal-to-noise ratio in the bursts. We propose to

employ

T = α × AER

max

(9)

as the threshold value for detection, in which 0 < α < 1 is the

parameter of the ERD algorithm. ERD algorithm can be described

as follows. First, the points of both functions of (6) and (7) with a

value higher than the threshold T are considered as the set of

candidates for the start points (denoted by

S) and the set of

candidates for end points (denoted by ℰ), respectively. The sets S

and E are processed as follows. In each neighbourhood of L

samples, if there are more than one candidate points in S, only the

candidate with the maximum value of

(k) is kept in the set.

Similarly, in each neighbourhood of L samples, if there are more

than one candidate points in ℰ, only the candidate with the

maximum value of ER

(k) is kept in the set.

In the next step, by starting from the smallest element t

in ℰ,

the closest point

from S with the condition t

< t

is selected and

the detector labels the presence of burst [t

, t

] in w

. Then, in

addition to removing t

and t

from ℰ and S, respectively, all the

elements in S which are smaller than t

are removed from S. If

there is no t

in S with the condition t

< t

, t

in ℰ is removed and

no burst will detect corresponding to this point. This process is

repeated until

ℰ is empty. ERD algorithm is shown in Algorithm 1

(see Fig. 3)

In general, since the detection is performed in the non-

cooperative environment, there is no prior information about the

lengths of the bursts and the guards. Assume that the length L is

less than the burst length. So, during the computation of ER

(k)

and ER

(k), one of the following events may occur:

i. Both adjacent windows are entirely in burst samples or they

are completely in guard samples.

ii. One of the windows includes only guard samples and the other

window includes only burst samples.

iii. There is only one transition (from 0 to 1, or vice versa) in w

corresponding to the samples of one of the windows.

iv. There are more than one transition in w

corresponding to the

samples of one of the windows.

There are no challenges in the case of events i and ii. In fact,

most of the detection errors occur when event iii or event iv take

place. Error in case iii causes the burst length be estimated larger or

smaller than its real length. Event iv occurs when the guard length

is too short compared to the window length L. In this case, the

detection algorithm may miss the guard and label the noise-only

samples as the burst samples. As a result, the length of the sliding

Fig. 1 Example of dissimilar w

and w

Fig. 2 ERD functions for finding start and end time of bursts

IET Commun., 2019, Vol. 13 Iss. 7, pp. 863-872

865

Authorized licensed use limited to: BEIJING INSTITUTE OF TECHNOLOGY. Downloaded on September 02,2020 at 05:32:37 UTC from IEEE Xplore. Restrictions apply.

评论收藏

内容反馈

版权申诉