
2
the correct support set are included in the estimated support
set. The computational complexity of OMP strategies depends
on the number of iterations needed for exact reconstruction:
standard OMP always runs through K iterations, and there-
fore its reconstruction complexity is roughly O (KmN ) (see
Section IV-C for details). This complexity is significantly
smaller than that of LP methods, especially when the signal
sparsity level K is small. However, the pursuit algorithms do
not have provable reconstruction quality at the level of LP
methods. For OMP techniques to operate successfully, one
requires that the correlation between all pairs of columns
of Φ is at most 1/2K [8], which by the Gershgorin Circle
Theorem [9] represents a more restrictive constraint than
the RIP. The ROMP algorithm [10] can reconstruct all K-
sparse signals provided that the RIP holds with parameter
δ
2K
≤ 0.06/
√
log K, which strengthens the RIP requirements
for l
1
-linear programming by a factor of
√
log K.
The main contribution of this paper is a new algorithm,
termed the subspace pursuit (SP) algorithm. It has provable
reconstruction capability comparable to that of LP methods,
and exhibits the low reconstruction complexity of matching
pursuit techniques for very sparse signals. The algorithm can
operate both in the noiseless and noisy regime, allowing
for exact and approximate signal recovery, respectively. For
any sampling matrix Φ satisfying the RIP with a constant
parameter independent of K, the SP algorithm can recover
arbitrary K-sparse signals exactly from its noiseless mea-
surements. When the measurements are inaccurate and/or the
signal is not exactly sparse, the reconstruction distortion is
upper bounded by a constant multiple of the measurement
and/or signal perturbation energy. For very sparse signals
with K ≤ const ·
√
N, which, for example, arise in certain
communication scenarios, the computational complexity of the
SP algorithm is upper bounded by O (mNK), but can be
further reduced to O (mN log K) when the nonzero entries
of the sparse signal decay slowly.
The basic idea behind the SP algorithm is borrowed from
coding theory, more precisely, the A
∗
order-statistic algo-
rithm [11] for additive white Gaussian noise channels. In
this decoding framework, one starts by selecting the set of
K most reliable information symbols. This highest reliability
information set is subsequently hard-decision decoded, and
the metric of the parity checks corresponding to the given
information set is evaluated. Based on the value of this
metric, some of the low-reliability symbols in the most reliable
information set are changed in a sequential manner. The
algorithm can therefore be seen as operating on an adaptively
modified coding tree. If the notion of “most reliable symbol”
is replaced by “column of sensing matrix exhibiting highest
correlation with the vector y”, the notion of “parity-check
metric” by “residual metric”, then the above method can be
easily changed for use in CS reconstruction. Consequently,
one can perform CS reconstruction by selecting a set of K
columns of the sensing matrix with highest correlation that
span a candidate subspace for the sensed vector. If the distance
of the received vector to this space is deemed large, the
algorithm incrementally removes and adds new basis vectors
according to their reliability values, until a sufficiently close
candidate word is identified. SP employs a search strategy in
which a constant number of vectors is expurgated from the
candidate list. This feature is mainly introduced for simplicity
of analysis: one can easily extend the algorithm to include
adaptive expurgation strategies that do not necessarily operate
on fixed-sized lists.
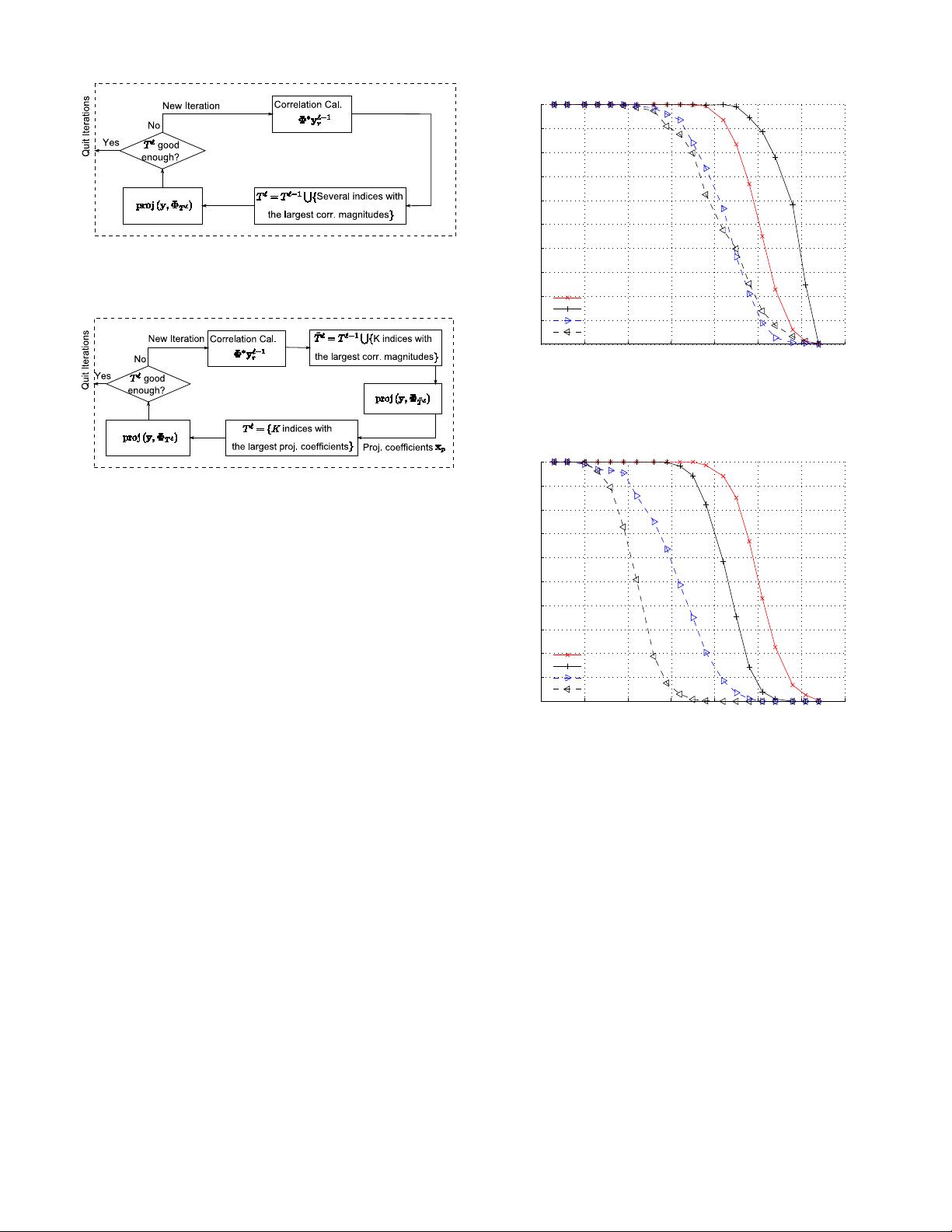
In compressive sensing, the major challenge associated with
sparse signal reconstruction is to identify in which subspace,
generated by not more than K columns of the matrix Φ,
the measured signal y lies. Once the correct subspace is
determined, the non-zero signal coefficients are calculated by
applying the pseudoinversion process. The defining character
of the SP algorithm is the method used for finding the K
columns that span the correct subspace: SP tests subsets of
K columns in a group, for the purpose of refining at each
stage an initially chosen estimate for the subspace. More
specifically, the algorithm maintains a list of K columns of Φ,
performs a simple test in the spanned space, and then refines
the list. If y does not lie in the current estimate for the correct
spanning space, one refines the estimate by retaining reliable
candidates, discarding the unreliable ones while adding the
same number of new candidates. The “reliability property” is
captured in terms of the order statistics of the inner products
of the received signal with the columns of Φ, and the subspace
projection coefficients.
As a consequence, the main difference between ROMP and
the SP reconstruction strategy is that the former algorithm
generates a list of candidates sequentially, without back-
tracing: it starts with an empty list, identifies one or several
reliable candidates during each iteration, and adds them to
the already existing list. Once a coordinate is deemed to be
reliable and is added to the list, it is not removed from it
until the algorithm terminates. This search strategy is overly
restrictive, since candidates have to be selected with extreme
caution. In contrast, the SP algorithm incorporates a simple
method for re-evaluating the reliability of all candidates at
each iteration of the process.
At the time of writing this manuscript, the authors became
aware of the related work by J. Tropp, D. Needell and R. Ver-
shynin [12], describing a similar reconstruction algorithm. The
main difference between the SP algorithm and the CoSAMP
algorithm of [12] is in the manner in which new candidates are
added to the list. In each iteration, in the SP algorithm, only K
new candidates are added, while the CoSAMP algorithm adds
2K vectors. This makes the SP algorithm computationally
more efficient, but the underlying analysis more complex. In
addition, the restricted isometry constant for which the SP
algorithm is guaranteed to converge is larger than the one
presented in [12]. Finally, this paper also contains an analysis
of the number of iterations needed for reconstruction of a
sparse signal (see Theorem 6 for details), for which there is
no counterpart in the CoSAMP study.
The remainder of the paper is organized as follows. Sec-
tion II introduces relevant concepts and terminology for de-
scribing the proposed CS reconstruction technique. Section III
contains the algorithmic description of the SP algorithm, along
with a simulation-based study of its performance when com-
pared with OMP, ROMP, and LP methods. Section IV contains

 Matlab重构算法.rar (10个子文件)
Matlab重构算法.rar (10个子文件)  Matlab重构算法
Matlab重构算法  SP算法
SP算法  SP.pdf 455KB
SP.pdf 455KB SP.m 1KB
SP.m 1KB software
software  Demo_CS_SP.m 3KB
Demo_CS_SP.m 3KB Demo_CS_CoSaMP.m 3KB
Demo_CS_CoSaMP.m 3KB Demo_CS_IHT.m 3KB
Demo_CS_IHT.m 3KB lena.bmp 65KB
lena.bmp 65KB Demo_CS_IRLS.m 3KB
Demo_CS_IRLS.m 3KB Demo_CS_OMP.m 3KB
Demo_CS_OMP.m 3KB Demo_CS_GBP.m 8KB
Demo_CS_GBP.m 8KB CS Recovery Algorithms.pdf 418KB
CS Recovery Algorithms.pdf 418KB




 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助 
 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜

 信息提交成功
信息提交成功



- 1
- 2
- 3
- 4
前往页