Aldebaro Klautau - 11/22/05. Page 4.
Roughly speaking: a good parametric representation for a speech recognition system tries to
eliminate the influence of the source (the system must give the same "answer" for a high pitch
female voice and for a low pitch male voice), and characterize the filter. The problem is:
source e(n) and filter impulse response h(n) are convoluted. Then we need deconvolution in
speech recognition applications. Mathematically:
In the time domain, convolution: source * filter = speech,
e(n) * h(n) = x(n). (1)
In the frequency domain, multiplication: source x filter = speech,
E(z) H(z) = X(z). (2)
How can we make the deconvolution ? Cepstral analysis is an alternative.
è Working in the frequency domain, use the logarithm to transform the multiplication in (2)
into a summation (obs: log ab = log a + log b). It is not easy to separate (to filter) things that
are multiplied as in (2), but it is easy to design filters to separate things that are parcels of a
sum as below:
C(z) = log X(z) = log E(z) + log H(z). (3)
We hope that H(z) is mainly composed by low frequencies and E(z) has most of its
energy in higher frequencies, in a way that a simple low-pass filter can separate H(z) from E(z)
if we were dealing with E(z) + H(z). In fact, let us suppose for the sake of simplicity that we
have, instead of (3), the following equation:
C
o
(z) = E(z) + H(z). (4)
We could use a linear filter to eliminate E(z) and then calculate the Z-inverse transform
to get a time-sequence c
o
(z). Notice that in this case, co(z) would have dimension of time
(seconds, for example).
Having said that, let us now face our problem: the log operation in (3). Log is a non-
linear operation and it can "create" new frequencies. For example, expanding the log of a
cosine in Taylor series shows that harmonics are created. So, even if E(z) and H(z) are well
separated in the frequency domain, log E(z) and log H(z) could eventually have considerable
overlap. Fortunately, that is not the case in practice for speech processing. The other point is
that, because of the log operation, the Z-inverse of C(z) in (3) has NOT the dimension of time
as in (4). We call cepstrum the Z-inverse of C(z) and its dimension is quefrency (a time
domain parameter).
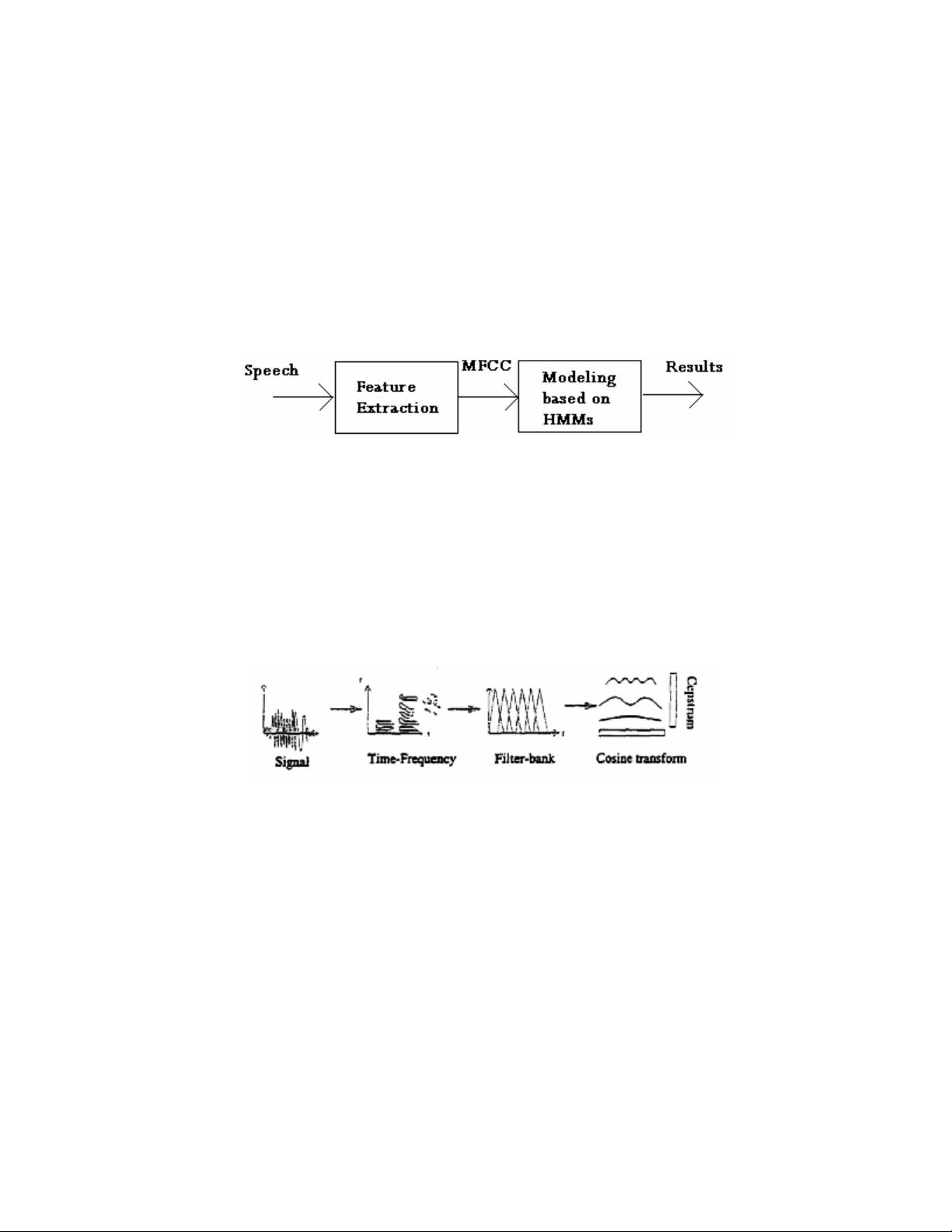
è There are 2 basic types of cepstrum: complex cepstrum and real cepstrum. Besides, there
are two ways of calculating the real cepstrum (used in speech processing because phase is not
important): LPC cepstrum and FFT cepstrum.
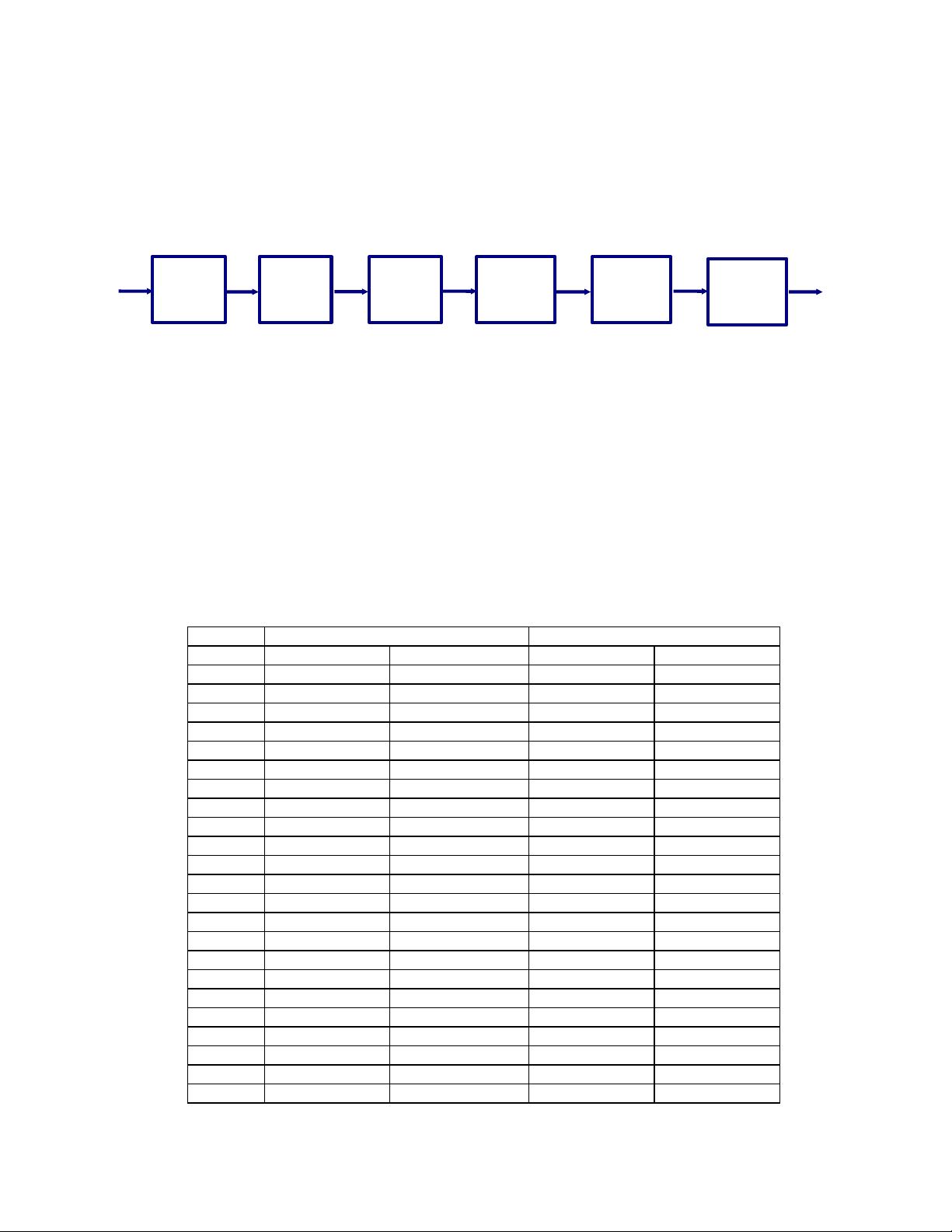
LPC cepstrum: the cepstral coefficients are obtained from the LPC coefficients
FFT cepstrum: from a FFT
Which one is better ? The most widely parametric representation for speech recognition is the
FFT cepstrum derived based on a mel scale [Davis, 80].

 mfcc.rar (1个子文件)
mfcc.rar (1个子文件)  mfcc.pdf 199KB
mfcc.pdf 199KB

 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助 
 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜

 信息提交成功
信息提交成功