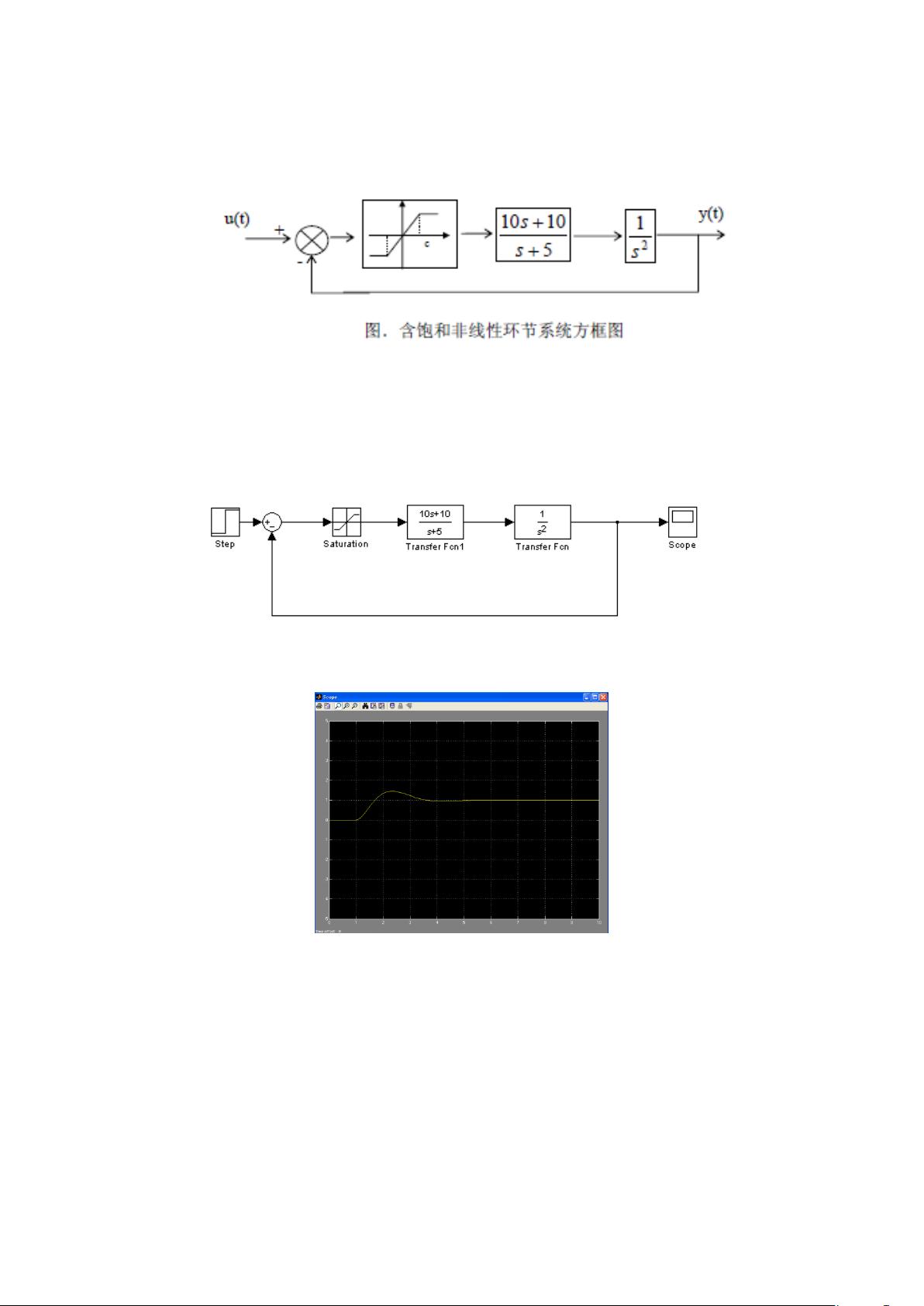
在MATLAB环境中，遗传算法（Genetic Algorithm, GA）是一种基于生物进化理论的全局优化方法，常用于解决复杂的、多模态的优化问题。在这个"matlab.rar_目标函数编程_遗传 整数_遗传算法 整数"的资源中，我们可以看到作者使用MATLAB编程实现了一个针对目标函数优化的遗传算法，特别地，该算法适用于寻找最大值，并且解必须是非负整数。
遗传算法的基本思想源于自然界中的物种进化过程，包括选择、交叉和变异等操作。在MATLAB中实现遗传算法时，通常会经历以下步骤：
1. 初始化种群：随机生成一定数量的个体，每个个体代表一个可能的解决方案，也就是一个整数向量。
2. 适应度函数：定义目标函数，也就是需要最大化或最小化的函数。在这个例子中，目标函数是求最大值，所以需要对每个个体的适应度进行评估，通常适应度值越高，表示个体的解决方案越好。
3. 选择操作：根据适应度值，按照某种策略（如轮盘赌选择、锦标赛选择等）选择一部分个体进入下一代。
4. 交叉操作：对被选中的个体进行交叉，生成新的个体。在整数优化中，可以采用部分匹配交叉、单点交叉或多点交叉等方式。
5. 变异操作：对新生成的个体进行随机变异，增加种群多样性。整数变异可以是随机改变某个位置的数值，或者交换两个位置的数值。
6. 终止条件：当达到预定的迭代次数、目标函数阈值或适应度值不再显著提升时，停止算法并返回当前最佳解。
在压缩包中的“实验七 李献.doc”文档，很可能是对这个遗传算法实现的详细说明，包括具体代码实现、算法参数设置、实验结果分析等内容。通过阅读这份文档，你可以更深入地理解如何在MATLAB中编写遗传算法程序，以及如何调整参数以适应特定的目标函数和整数解约束。
这个资源提供了使用MATLAB进行遗传算法整数优化的一个实例，对于学习和实践优化算法，特别是需要寻找非负整数解的问题，是非常有价值的参考资料。通过理解和应用这些知识，你可以解决实际工程中的各种优化问题，比如电路设计、生产调度、投资组合优化等。
评论0