
Chapter 3
Cramer-Rao Lower Bound
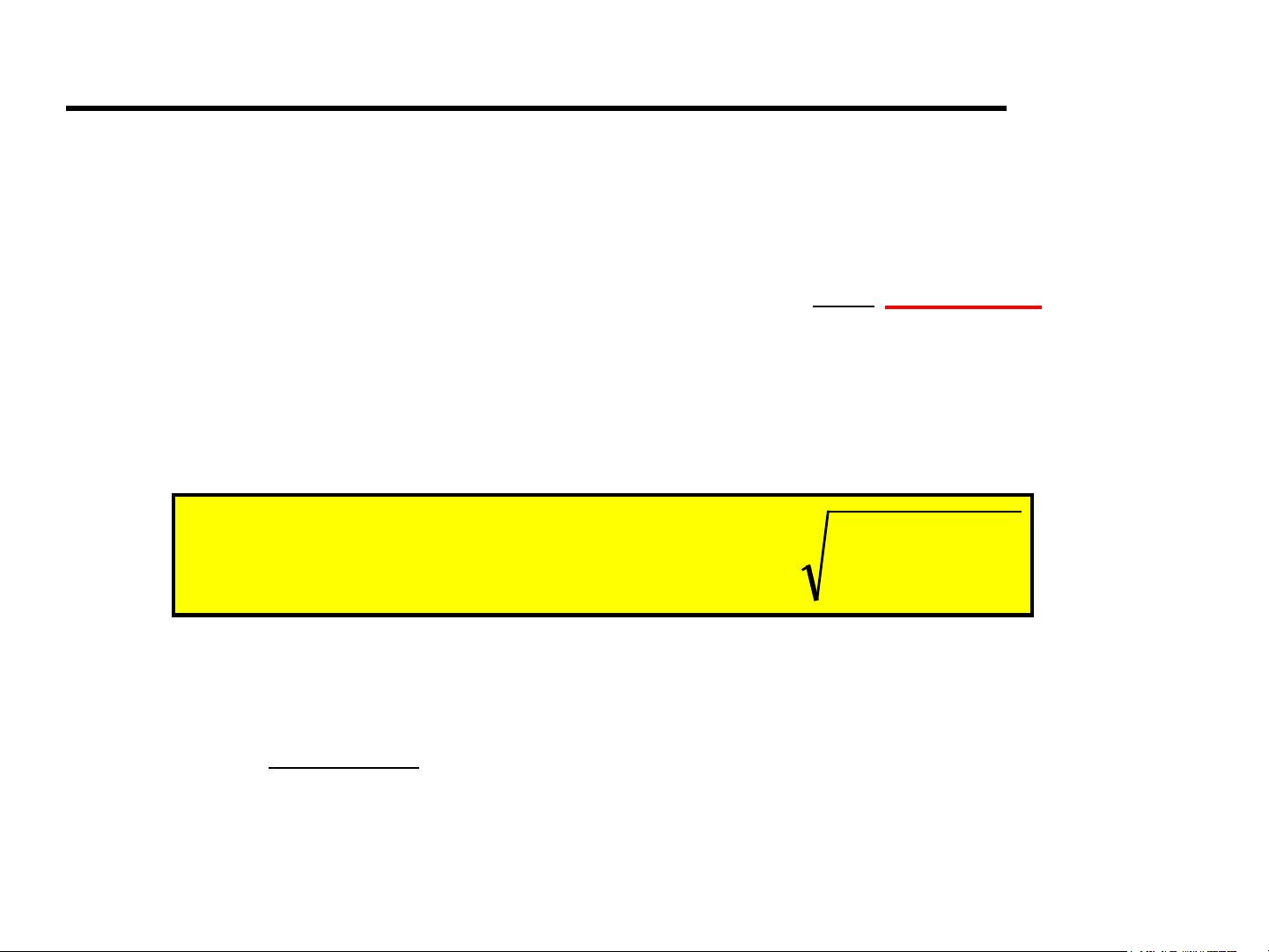
Abbreviated: CRLB or sometimes just CRB
CRLB is a lower bound on the variance of any unbiased
estimator:
The CRLB tells us the best we can ever expect to be able to do
(w/ an unbiased estimator)
then, ofestimator unbiased an is
ˆ
If
θθ
)()()()(
ˆˆˆ
2
ˆ
θθσθθσ
θθθ
θ
CRLBCRLB ≥⇒≥
What is the Cramer-Rao Lower Bound

1. Feasibility studies ( e.g. Sensor usefulness, etc.)
• Can we meet our specifications?
2. Judgment of proposed estimators
• Estimators that don’t achieve CRLB are looked
down upon in the technical literature
3. Can sometimes provide form for MVU est.
4. Demonstrates importance of physical and/or signal
parameters to the estimation problem
e.g. We’ll see that a signal’s BW determines delay est. accuracy
⇒ Radars should use wide BW signals
Some Uses of the CRLB
Q: What determines how well you can estimate
θ
?
Recall: Data vector is x
3.3 Est. Accuracy Consideration
samples from a random
process that depends
on an θ
⇒ the PDF describes that
dependence: p(x;
θ
)
Clearly if p(x;
θ
) depends strongly/weakly on θ
…we should be able to estimate θ well/poorly.
See surface plots vs. x & θ for 2 cases:
1. Strong dependence on θ
2. Weak dependence on θ
⇒ Should look at p(x;
θ
) as a function of θ for
fixed
value of observed data x
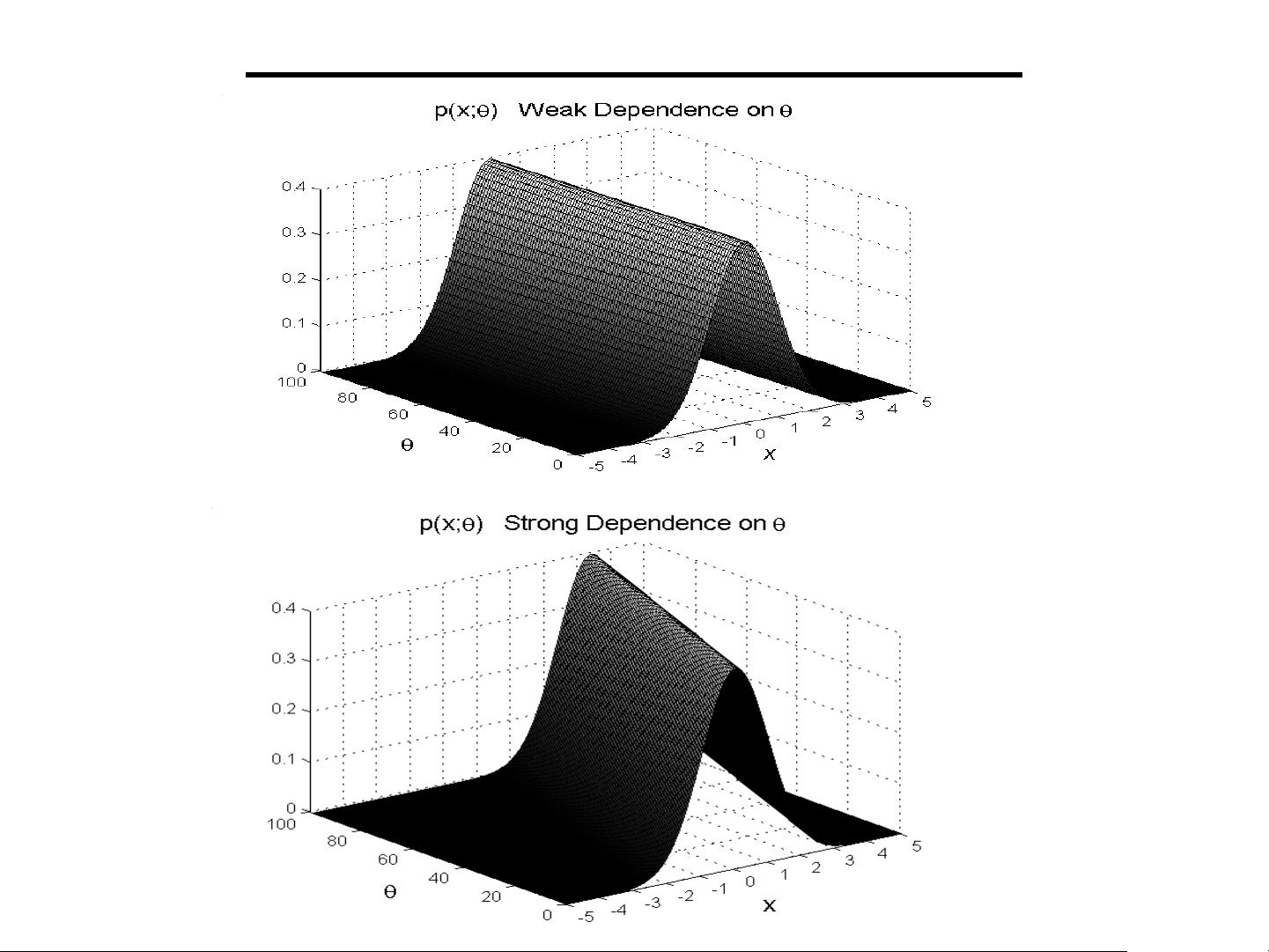
Surface Plot Examples of p(x;
θ
)















