
ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ
“ΨΗΦΙΑΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ & ΔΙΚΤΥΑ”
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ - ΤΜΗΜΑ ΔΙΔΑΚΤΙΚΗ ΤΗΣ
ΤΕΧΝΟΛΟΓΙΑΣ & ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ
Μοντέλα Τηλεπικοινωνιακής Κίνησης
Δημαρτίκας Ν. Ιωάννης Α.Μ.:ΜΕ/07045
Κουρδουμπάς Γ. Σταμάτιος Α.Μ.:ΜΕ/07051
ΠΕΙΡΑΙΑΣ
ΜΑΙΟΣ 2008
1
η
Εργαστηριακή Άσκηση
«Αποτίμηση επίδοσης επικοινωνιακού πρωτοκόλλου με τη
χρήση Μαρκοβιανού μοντέλου ανάλυσης»

Εισαγωγή
Στην συγκεκριμένη εργαστηριακή άσκηση θα μελετήσουμε την απόδοση του
επικοινωνιακού πρωτοκόλλου slotted Aloha κάνοντας χρήση του Μαρκοβιανού
μοντέλου ανάλυσης.
Αρχικά θεωρούμε πεπερασμένο αριθμό Μ σταθμών οι οποίοι συνδέονται στον δίαυλο
και μπορούν να ανταλλάσσουν πληροφορίες χρησιμοποιώντας το πρωτόκολλο slotted
ALOHA. Κάθε σταθμός είναι εφοδιασμένος με ένα καταχωρητή εξόδου (οutput
buffer) χωρητικότητας ενός πακέτου. Ο άξονας του χρόνου διαιρείται σε slots όπου
κάθε slot αποτελεί το βήμα μετάβασης στο Μαρκοβιανό μοντέλο ανάλυσης. Κάθε
σταθμός παράγει πακέτα σταθερού μήκους, των οποίων ο χρόνος μεταγωγής Τ είναι
ένα slot. Ένας σταθμός γεννά πακέτα στην αρχή κάθε slot ανεξάρτητα από τους
άλλους με πιθανότητα Pa ακολουθώντας ανεξάρτητη γεωμετρική κατανομή. Σε
περίπτωση ανεπιτυχούς μετάδοσης (σύγκρουσης) το πακέτο εισέρχεται στον output
buffer του σταθμού και ο σταθμός χαρακτηρίζεται ενεργός (backlogged). Σταθμοί με
άδειο output buffer χαρακτηρίζονται σαν ελεύθεροι (unbacklogged). Αν σε ένα
ενεργό σταθμό γεννηθεί ένα νέο πακέτο αυτό απορρίπτεται. Ένας ενεργός σταθμός
επιχειρεί να μεταδώσει ανεξάρτητα από τους άλλους στην αρχή κάθε slot με
πιθανότητα επανεκπομπής Pr επίσης ακολουθώντας ανεξάρτητη γεωμετρική
κατανομή. Θεωρούμε ότι ο χρόνος διάδοσης είναι αμελητέος.
Σύμφωνα με τις παραπάνω υποθέσεις η συμπεριφορά του slotted ALOHA μπορεί να
χαρακτηριστεί και να αναλυθεί από μια ομογενή Μαρκοβιανή αλυσίδα διακριτού
χρόνου. Σαν κατάσταση του συστήματος ορίζουμε τον αριθμό των ενεργών σταθμών
σε μια δεδομένη χρονική στιγμή. Ο αριθμός αυτός εκφράζεται από μια τυχαία
μεταβλητή Xt.
Πράγματι κάθε κατάσταση του συστήματος και για κάθε χρονική στιγμή t+1
εξαρτάται αποκλειστικά από την κατάσταση που βρισκόταν τη χρονική στιγμή t ,
αδιαφορώντας για την προϊστορία του συστήματος και τον τρόπο που προέκυψε η
τωρινή κατάσταση. Αυτό συμβαίνει γιατί οι ενεργοί χρήστες ανταγωνίζονται σε κάθε
slot ακολουθώντας διωνυμική διαδικασία η οποία είναι χωρίς μνήμη.
Πιο κάτω θα δούμε ότι παρουσιάζεται και ένας υποτυπώδης κώδικας σε java που
περιγράφει τον αλγόριθμο της όλης διαδικασίας που αναφέραμε πιο πάνω. Επίσης για
να μπορεί να γίνει μια αποτίμηση του υπό εξέταση μοντέλου αναφέρουμε κάποια
σημαντικά μεγέθη όπως το S (Throughput) που είναι το ποσοστό του χρόνου που ο
δίαυλος είναι απασχολημένος με επιτυχή μετάδοση πακέτων στην κατάσταση
ισορροπίας (απόδοση πρωτοκόλλου), το G ( κυκλοφορία) που είναι ο ρυθμός
εκπομπής / επανεκπομπής πακέτων στον δίαυλο στην κατάσταση ισορροπίας,
ανεξάρτητα εάν η μετάδοση είναι επιτυχημένη ή όχι, το Β (φορτίο) που είναι ο μέσος
αριθμός των ενεργών σταθμών στην κατάσταση ισορροπίας, το Sin (ρυθμός εισόδου)
που είναι η μέση τιμή των νέων αφίξεων πακέτων που γίνονται αποδεκτά από το
σύστημα στην κατάσταση ισορροπίας και το D (καθυστέρηση) που είναι η μέση τιμή
του χρόνου σε slots που απαιτείται για να μεταδοθεί ένα πακέτο στην κατάσταση
ισορροπίας.
Εν συνεχεία ολοκληρώνουμε την ανάλυση μας παρουσιάζοντας και αναλύοντας
κάποιες γραφικές παραστάσεις μεταξύ των μεγεθών που περιγράψαμε προηγουμένως,
προκείμενου να γίνει όσο πιο κατανοητή γίνεται η εν γένει συμπεριφορά του υπό
εξέταση πρωτοκόλλου μας.
Γραφικές παραστάσεις
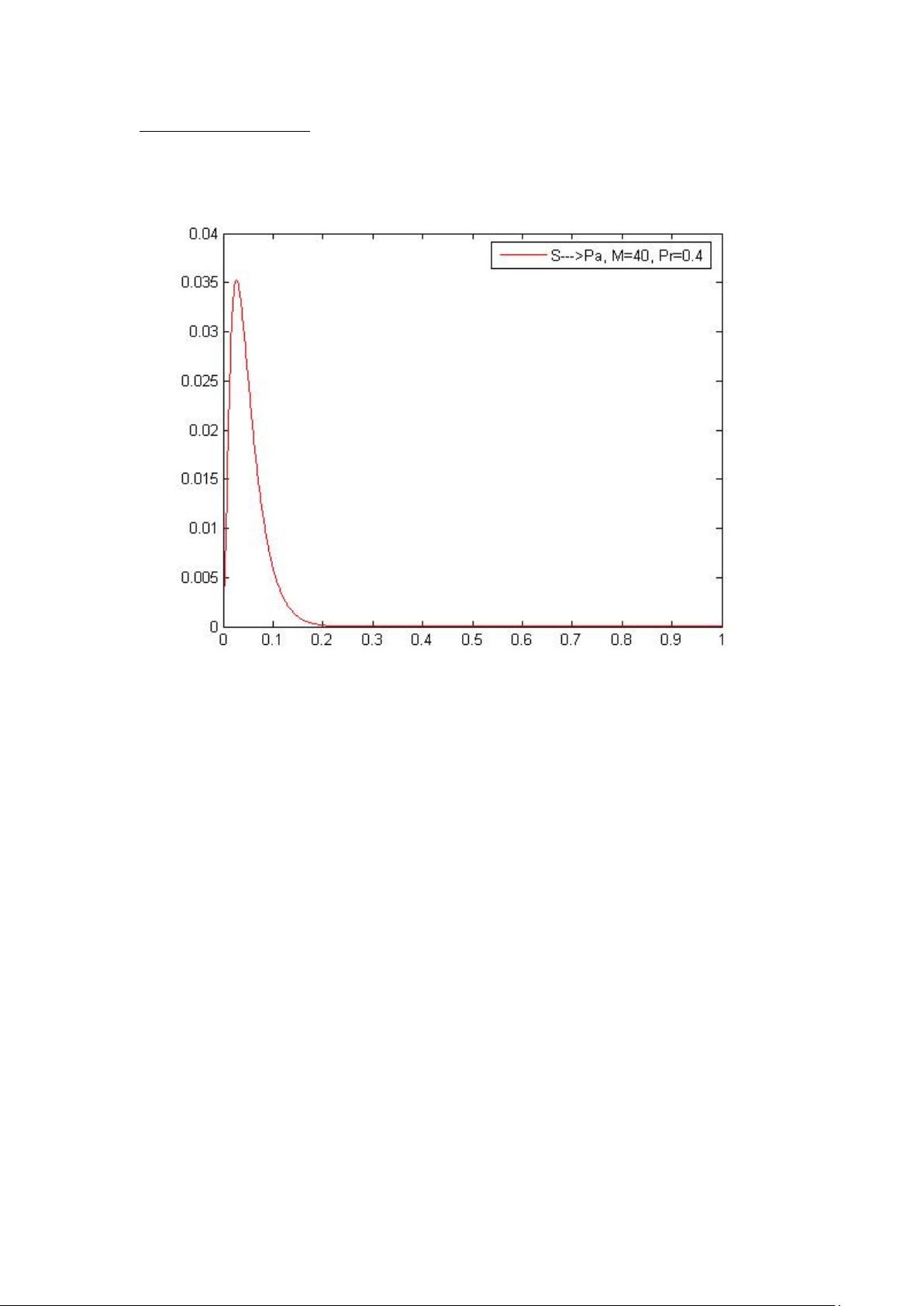
1) Για Pr = 0,4 και 40 κόμβους,
Αρχικά παρατηρούμε ότι η απόδοση του πρωτοκόλλου slotted aloha αυξάνεται μέχρι
το Pr= 0,05 περίπου όπου πιάνει και τη μέγιστη απόδοση του και εν συνεχεία
μειώνεται καθώς αυξάνεται η πιθανότητα άφιξης Pa. Στο σημείο όπου το Pa=0,21
περίπου η απόδοση του πρωτοκόλλου έχει πια μηδενιστεί και παραμένει μηδέν για
οποιαδήποτε τιμή του Pa από 0,21 έως 0,999. Επίσης μπορούμε να παρατηρήσουμε
ότι η μέγιστη απόδοση του πρωτοκόλλου με αυτές τις παραπάνω παραδοχές απέχει
πολύ από τι μέγιστη θεωρητική απόδοση του που είναι το 37%. Όπως φαίνεται μετά
βίας ξεπερνάει το 3,5%.

Αρχικά παρατηρούμε ότι όσο αυξάνεται η πιθανότητα άφιξης Pa το φορτίο Β
μειώνεται μέχρι μια τιμή του Pa= 0,1 περίπου, όπου από αυτό το σημείο και μετά το
φορτίο παραμένει σταθερό περίπου γύρω στο 20 για οποιαδήποτε τιμή του Pa μέχρι
το 0,999. Επίσης παρατηρούμε ότι το πρωτόκολλο μπορεί να αντέξει αρκετά
μικρότερο φορτίο σε σχέση με όταν το Pr είναι βέλτιστο. Με τις συγκεκριμένες
παραδοχές το φορτίο στη μέγιστη τιμή του φτάνει περίπου το 25,5 ενώ με βέλτιστο Pr
όπως θα δούμε και στη συνέχεια η τιμή αυτή φτάνει το 40.
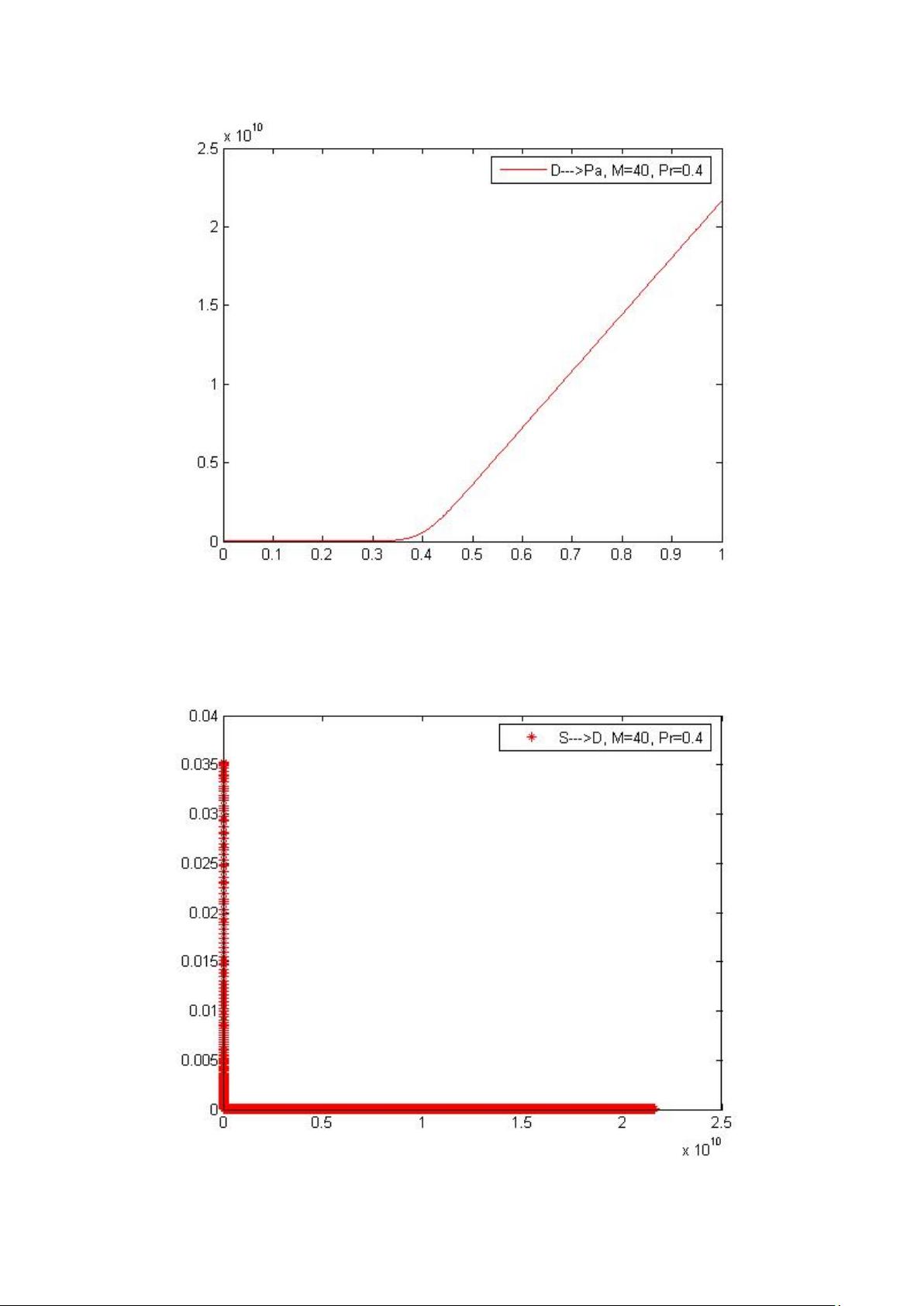
Αρχικά παρατηρούμε ότι για πιθανότητα άφιξης Pa μέχρι και Pa=0,35 περίπου η
καθυστέρηση παραμένει σταθερή και πάρα πολύ μικρή. Εν συνεχεία όσο αυξάνεται
το Pa αυξάνεται και η καθυστέρηση και όπως θα δούμε και στην επόμενη γραφική
παράσταση μειώνεται η απόδοση του πρωτοκόλλου.



















评论0