
Tutorial on Gabor Filter s
Javier R. Movellan

1 The Temporal (1-D) Gabor Filter
Gabor filters can serve as excellent band-pass filters for unidimensional sig nals (e.g.,
sp e e ch). A complex Gabor filter is defined as the product of a Gaussian kernel times
a complex sinusoid, i.e.
g(t) = ke
jθ
w(at)s(t) (1)
where
w(t) = e
−πt
2
(2)
s(t) = e
j(2πf
o
t)
(3)
e
jθ
s(t)e
j(2πf
o
t+θ)
=
sin(2πf
o
t + θ), j cos(2πf
o
t + θ)
(4)
Here k, θ, f
o
are filter parameters. We can think of the complex Gabor filter as two
out of phase filter s continently allocated in the real and complex part of a complex
function, the real part holds the filter
g
r
(t) = w(t) sin(2πf
o
t + θ) (5)
and the imaginary part holds the filter
g
i
(t) = w(t) cos(2πf
o
t + θ) (6)
1.1 Frequency Response
Taking the Fourier transform
ˆg(f) = ke
jθ
Z
∞
−∞
e
−j2πft
w(at)s(t) dt = ke
jθ
Z
∞
−∞
e
−j2π(f−f
o
)t
w(at)dt (7)
=
k
a
e
jθ
ˆw(
f − f
o
a
) (8)
where
ˆw(f) = w(f) = e
−πf
2
(9)
1.2 Gabor Energy Filters
The re al and imaginary components of a complex Gabor filter are phase sensitive,
i.e., as a consequence their respons e to a sinusoid is another sinusoid (see Figure
1.2). By ge tting the magnitude of the output (square root of the sum of squared
real and imaginary outputs) we can get a response that phase insensitive and thus
unmodulated positive respo ns e to a target sinusoid input (see Figure 1.2). In some
cases it is useful to compute the over all output of the two out of phase filters.
One commo n way of doing so is to add the squared o utput (the energy) of each
filter, equivalently we can get the magnitude. This corresponds to the magnitude
(more precisely the squared magnitude) of the complex Gabor filter output. In the
frequency domain, the magnitude of the response to a particular frequency is simply
the magnitude of the complex Fourier transform, i.e.
kg(f )k =
k
a
ˆw(
f − f
o
a
) (10)
Note this is a Gaussian function centered at f
0
and with width proportional to a.
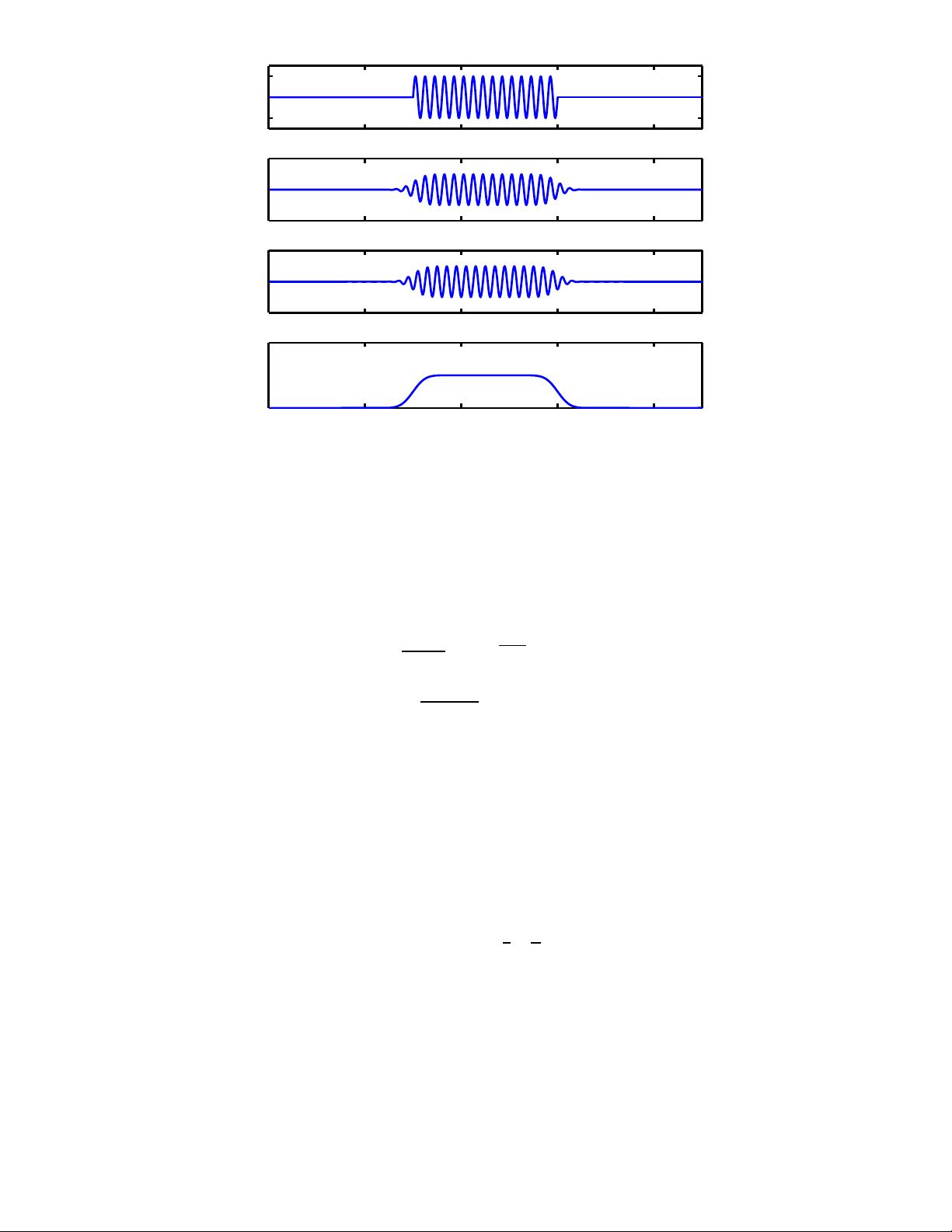
0 2 4 6 8
−1
0
1
0 2 4 6 8
−50
0
50
0 2 4 6 8
−50
0
50
0 2 4 6 8
0
50
Figure 1: Top: An input signal. Second: Output of Gabor filter (cosine carrier).
Third: Output of Gabor Filter in quadrature (sine carrier); Fourth: Output of
Gabor Energy Filter
1.2.1 Bandwidth and Peak Response
Thus the peak filter response is at f
o
. To get the half-magnitude bandwidth ∆
f
note
ˆw(
f − f
o
a
) = e
−π
f−f
o
a
2
= 0.5 (11)
Thus the half peak magnitude is achieved for
f − f
o
±
p
a
2
log 2π = 0.4 697 a ≈ 0.5 a (12)
Thus the half-magnitude bandwidth is (2)(0.4697 )a) which is approximately eq ual
to a. Thus a can be interpreted as the half-magnitude filter bandwidth.
1.3 Elimi nating the DC response
Depending on the value of f
o
and a the filter may have a lar ge DC response. A
popular approach to get a zero DC response is to subtract the output of a low-pass
Gaussian filter,
h(t) = g(t) − c w(bt) = ke
jθ
w(at)s(t) − c w(bt) (13)
Thus
ˆ
h(f) = ˆg(f ) −
c
b
ˆw(
f
b
) (14)

To get a zero DC response we need
c
b
ˆw(0) = ˆg(0) (15)
c = bˆg(0) = b
k
a
e
jθ
ˆw(
f
o
a
) (16)
where we used the fact that ˆw(f
o
) = ˆw(−f
o
) Thus,
h(t) = g(t) − b ˆg(0) = ke
jθ
w(at)s(t) −
b
a
ˆw(
f
o
a
)w(bt)
(17)
ˆ
h(f) =
k
a
e
jθ
ˆw(
f − f
o
a
) − ˆw(
f
o
a
) ˆw(
f
b
)
(18)
It is convenient, to let b = a, in which case
h(t) = ke
jθ
w(at)
s(t) − ˆw(
f
o
a
)
(19)
h(f) =
k
a
e
jθ
ˆw(
f − f
o
a
) − ˆw(
f
o
a
) ˆw(
f
a
)
(20)
2 The Spatial (2-D) Gabor Filter
Here is the formula of a co mplex Gabor function in space domain
g(x, y) = s(x, y) w
r
(x, y) (21)
where s(x, y) is a complex sinusoid, known as the carrier, and w
r
(x, y) is a 2-D
Gaussian-shaped function, known as the envelope.
2.1 The complex sinusoid carrier
The complex sinusoid is defined as follows,
1
s(x, y) = exp (j (2π(u
0
x + v
0
y) + P )) (22)
where (u
0
, v
0
) and P define the spatial frequency and the phase of the sinusoid
respectively.
We can think of this sinusoid as two separate real functions, conveniently allocated
in the real and imaginary part of a complex function (see Figure 1).
1
An offset constant parameter for s(x, y) will be introduced later, to compensate the
DC-comp onent of this sinusoid. Refer to the appendix for detailed explanation.
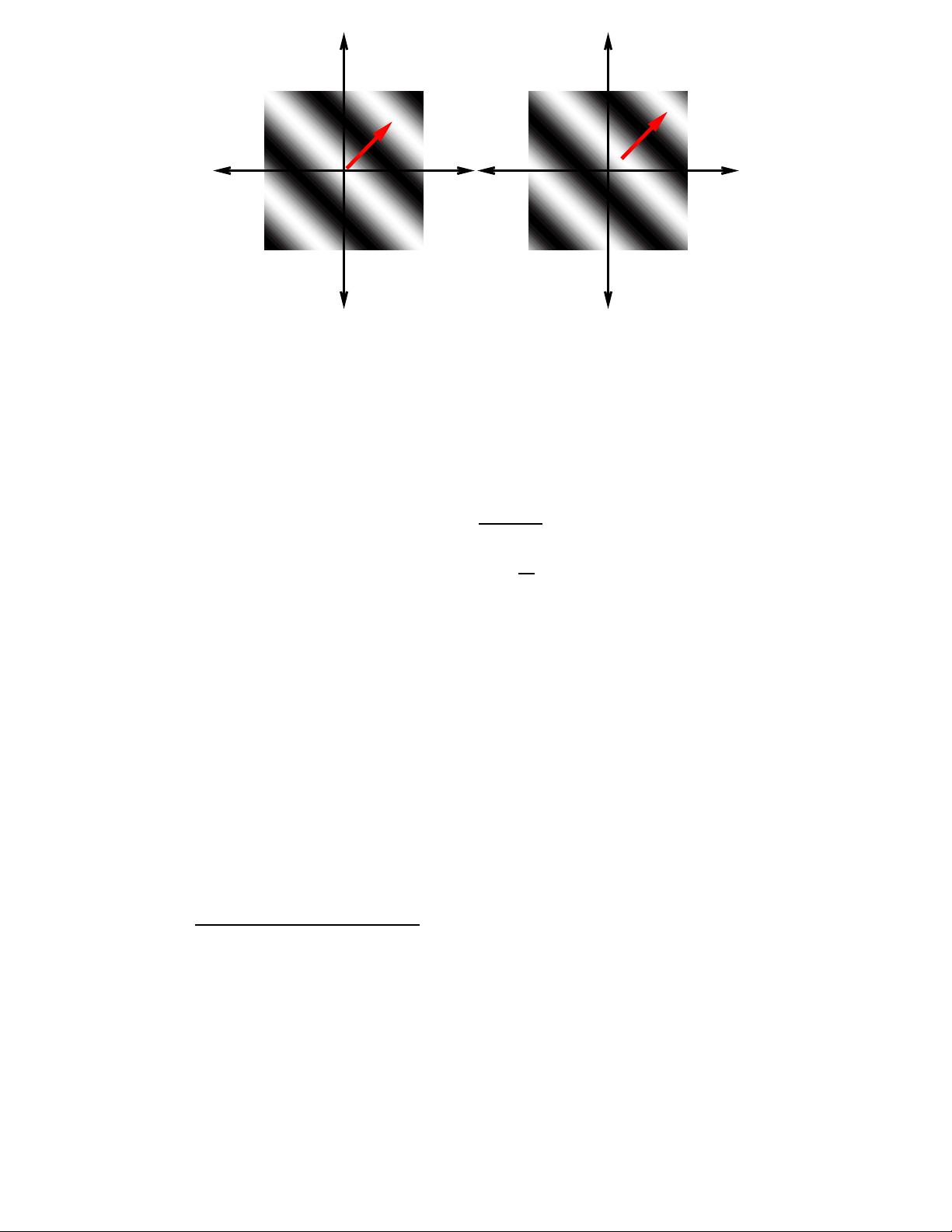
Figure 2: The real and imaginary parts of a complex sinusoid. The ima ges are
128 × 128 pixels. The parameters are: u
0
= v
0
= 1/80 cycles/pixel, P = 0 deg.
The real part and the imagina ry part of this sinuso id are
Re (s(x, y)) = cos (2π(u
0
x + v
0
y) + P )
Im (s(x, y)) = sin (2π(u
0
x + v
0
y) + P )
(23)
The parameters u
0
and v
0
define the spatial frequency o f the sinusoid in Cartes ian
coordinates. This spatial frequency can also be expresse d in polar coordinates as
magnitude F
0
and direction ω
0
:
F
0
=
p
u
0
2
+ v
0
2
ω
0
= tan
−1
v
0
u
0
(24)
i.e.
u
0
= F
0
cos ω
0
v
0
= F
0
sin ω
0
(25)
Using this representation, the complex sinusoid is
s(x, y) = exp (j (2πF
0
(x cos ω
0
+ y sin ω
0
) + P )) (26)
2.2 The Gaussian envel ope
The Gaussian envelope looks as follows (see Figur e 2 ):
w
r
(x, y) = K e xp
−π
a
2
(x − x
0
)
r
2
+ b
2
(y − y
0
)
r
2
(27)
where (x
0
, y
0
) is the peak of the function, a and b are scaling parameters
2
of the
Gaussian, and the
r
subscript stands for a rotation operation
3
such that
(x − x
0
)
r
= (x − x
0
) cos θ + (y − y
0
) sin θ
(y − y
0
)
r
= −(x − x
0
) sin θ + (y −y
0
) cos θ
(28)
2
Note that the Gaussian gets smaller in the space domain, if a and b get larger.
3
This rotation is clockwise, the inverse of the counterclockwise rotation of the ellipse.















评论0