30573826Helmholtz.rar_wavelet helmholtz_傅里叶_傅里叶逆变换_逆变 频率_频率域时间域

2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
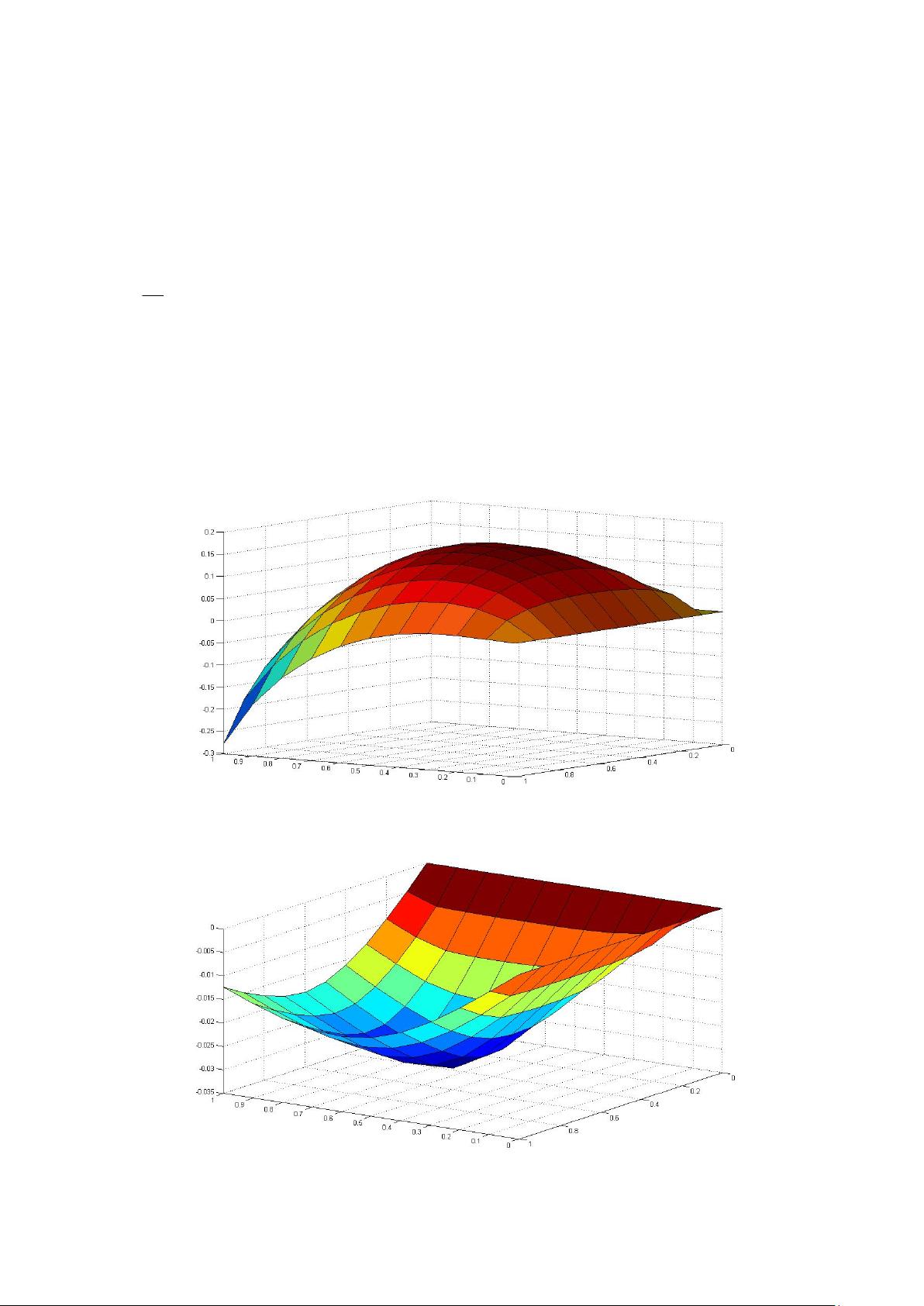
标题中的“30573826Helmholtz.rar_wavelet helmholtz_傅里叶_傅里叶逆变换_逆变 频率_频率域时间域”涉及了多个关键概念,包括赫尔姆霍茨方程(Helmholtz Equation)、小波变换(Wavelet Transform)、傅里叶变换(Fourier Transform)以及它们的逆变换。这些是信号处理和数值计算领域的核心内容。 赫尔姆霍茨方程是由德国物理学家赫尔姆霍茨提出的,用于描述波动现象的偏微分方程。在物理学、工程学及数学中,它常被用来分析声波、电磁波等波动问题。文件“Helmholtz方程的有限元解法.doc”可能详细介绍了如何利用有限元方法(Finite Element Method, FEM)求解该方程,这是一种数值计算技术,广泛应用于解决复杂的工程和物理问题。 “n=64,k=20.fig”可能是一个图形文件,显示了特定参数(n=64, k=20)下赫尔姆霍茨方程的解决方案或特性。数字“n”可能代表网格的节点数量,而“k”可能与波数或频率有关。 傅里叶变换是分析周期性和非周期性信号的基础工具,它将信号从时间域转换到频率域,揭示了信号的频率成分。文件“FEM2.m”可能是MATLAB脚本,用于实现傅里叶变换或其逆变换,即傅里叶逆变换。逆变换则将频率域的表示还原为原始的时间域信号。 小波变换是傅里叶变换的拓展,提供了一种在时间和频率上同时具有高分辨率的方法,适用于分析局部变化的信号。标签中的“wavelet_helmholtz”表明小波变换可能被用于解析或分析赫尔姆霍茨方程的问题。 “www.pudn.com.txt”可能是一个链接或者说明文件,指向一个资源下载网站,提供了更多与这些主题相关的资料。 这个压缩包包含的资料涵盖了波动理论、数值计算方法和信号分析的重要方面,对于学习和研究这些领域的人来说是非常有价值的资源。
 30573826Helmholtz.rar (4个子文件)
30573826Helmholtz.rar (4个子文件)  FEM2.m 3KB
FEM2.m 3KB Helmholtz方程的有限元解法.doc 880KB
Helmholtz方程的有限元解法.doc 880KB www.pudn.com.txt 218B
www.pudn.com.txt 218B n=64,k=20.fig 64KB
n=64,k=20.fig 64KB- 1

- 粉丝: 76
- 资源: 1万+
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- 基于Python和HTML的Chinese-estate-helper房地产爬虫及可视化设计源码
- 基于SpringBoot2.7.7的当当书城Java后端设计源码
- 基于Python和Go语言的开发工具集成与验证设计源码
- 基于Python与JavaScript的国内供应商管理系统设计源码
- aspose.words-20.12-jdk17
- 基于czsc库的Python时间序列分析设计源码
- 基于Java、CSS、JavaScript、HTML的跨语言智联平台设计源码
- 基于Java语言的day2设计源码学习与优化实践
- 基于浙江大学2024年秋冬学期软件安全原理与实践的C与Python混合语言设计源码
- 基于FastAPI和Vue3的表单填写与提交前后端一体化设计源码


 信息提交成功
信息提交成功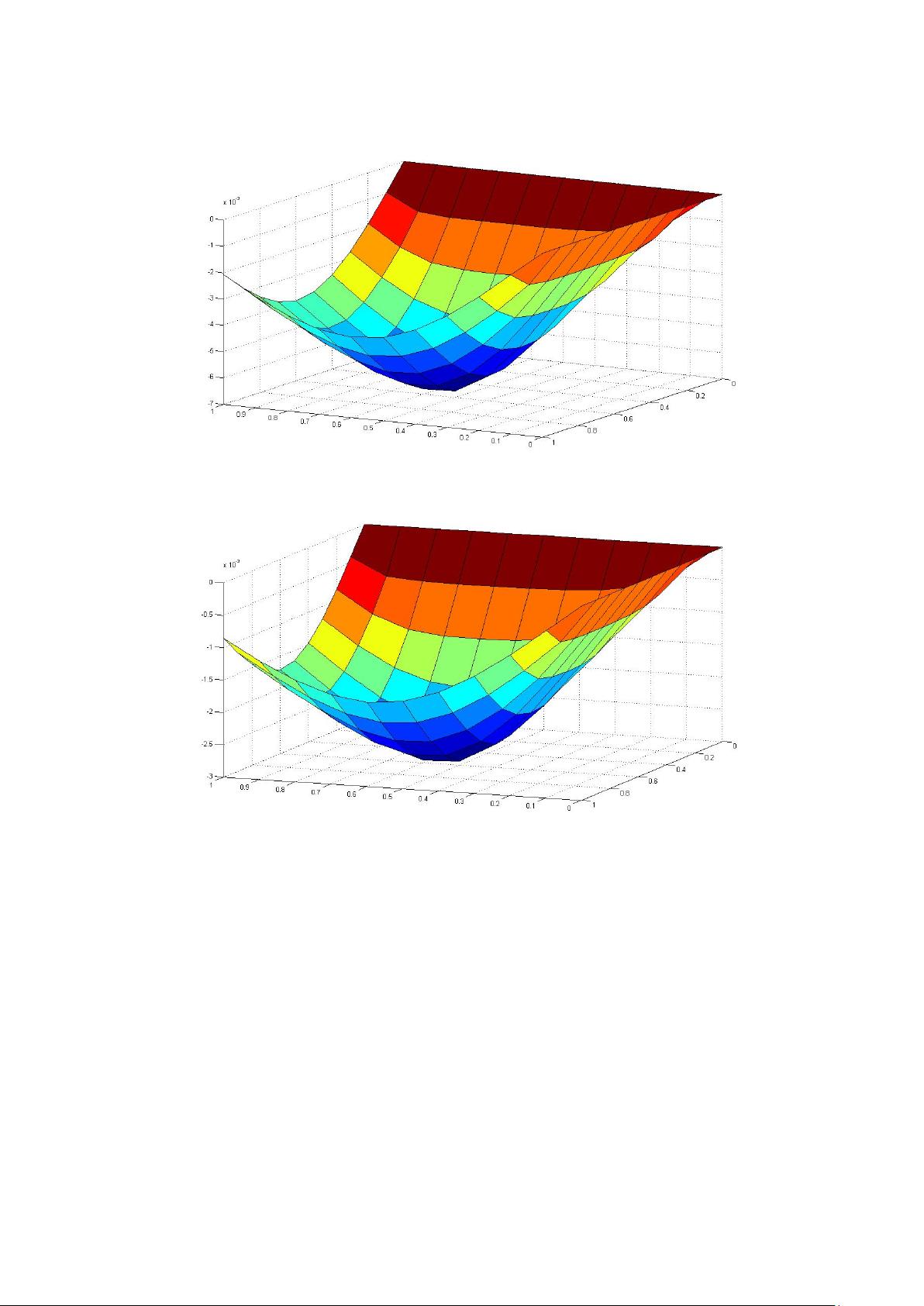
评论0