Kalman滤波在温度测量中的应用.rar_Kalman filter_kalman_kalman滤波预测_matlab_应用

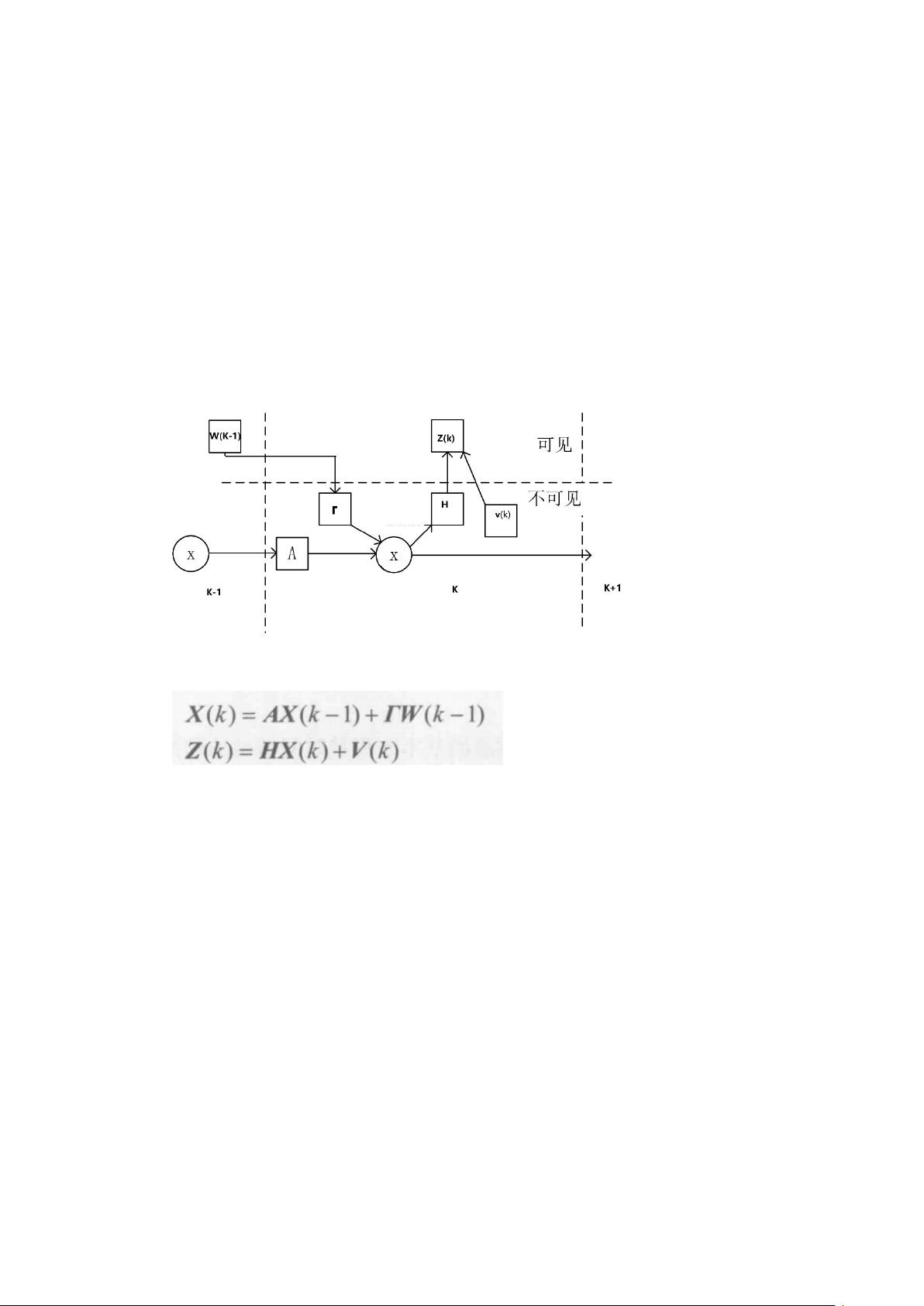
《卡尔曼滤波在温度测量中的应用》 卡尔曼滤波（Kalman Filter）是一种用于处理线性高斯系统的最优估计方法，广泛应用于各种领域的数据分析和预测，包括温度测量。在温度预测中，由于环境因素的复杂性和不确定性，数据往往包含噪声，卡尔曼滤波能够有效地从噪声中提取出真实信号，提高预测的准确性。 我们要理解卡尔曼滤波的基本原理。卡尔曼滤波基于概率统计理论，假设系统状态和观测数据都遵循高斯分布。它通过一系列迭代更新过程，对系统状态进行预测和校正，从而得到最佳估计。滤波过程包括两个主要步骤：预测（Prediction）和更新（Update）。 在预测阶段，卡尔曼滤波利用上一时刻的系统状态和动态模型来预测下一时刻的状态。动态模型通常由一组线性方程表示，描述了系统状态随时间的变化规律。例如，在温度预测中，我们可以考虑温度变化与时间、环境因素之间的关系。 在更新阶段，卡尔曼滤波会结合实际观测值和预测值，通过卡尔曼增益（Kalman Gain）调整预测状态，以减小噪声影响。卡尔曼增益是根据预测误差协方差和观测噪声协方差计算得出的，它决定了如何权衡预测信息和观测信息。 在实际应用中，如“KF.m”文件所示，我们可以使用MATLAB编写程序实现卡尔曼滤波。MATLAB提供了一套完整的工具箱，可以方便地构建和模拟卡尔曼滤波器。首先定义系统模型，包括状态转移矩阵、观测矩阵、过程噪声协方差和观测噪声协方差等参数。然后，通过循环迭代执行预测和更新步骤，处理观测数据。 对于“Kalman滤波在温度测量中的应用.docx”文档，可能详细介绍了如何将卡尔曼滤波应用于实际温度测量数据的处理过程，包括数据预处理、滤波器设计、滤波结果分析等。通过分析滤波后的数据，我们可以发现温度变化的趋势更加平滑，噪声被有效地消除，从而提高了温度预测的精度。 卡尔曼滤波在温度测量中的应用展示了其在处理噪声数据和进行实时预测方面的强大能力。通过MATLAB实现，我们能够直观地理解和应用这一算法，为实际工程问题提供解决方案。无论是科学研究还是工业应用，卡尔曼滤波都是一个不可或缺的工具，它能够帮助我们从混沌的数据中抽丝剥茧，揭示隐藏的真实信息。