十五个经典算法研究与总结、目录+索引（by_....rar_十五个经典算法_经典算法

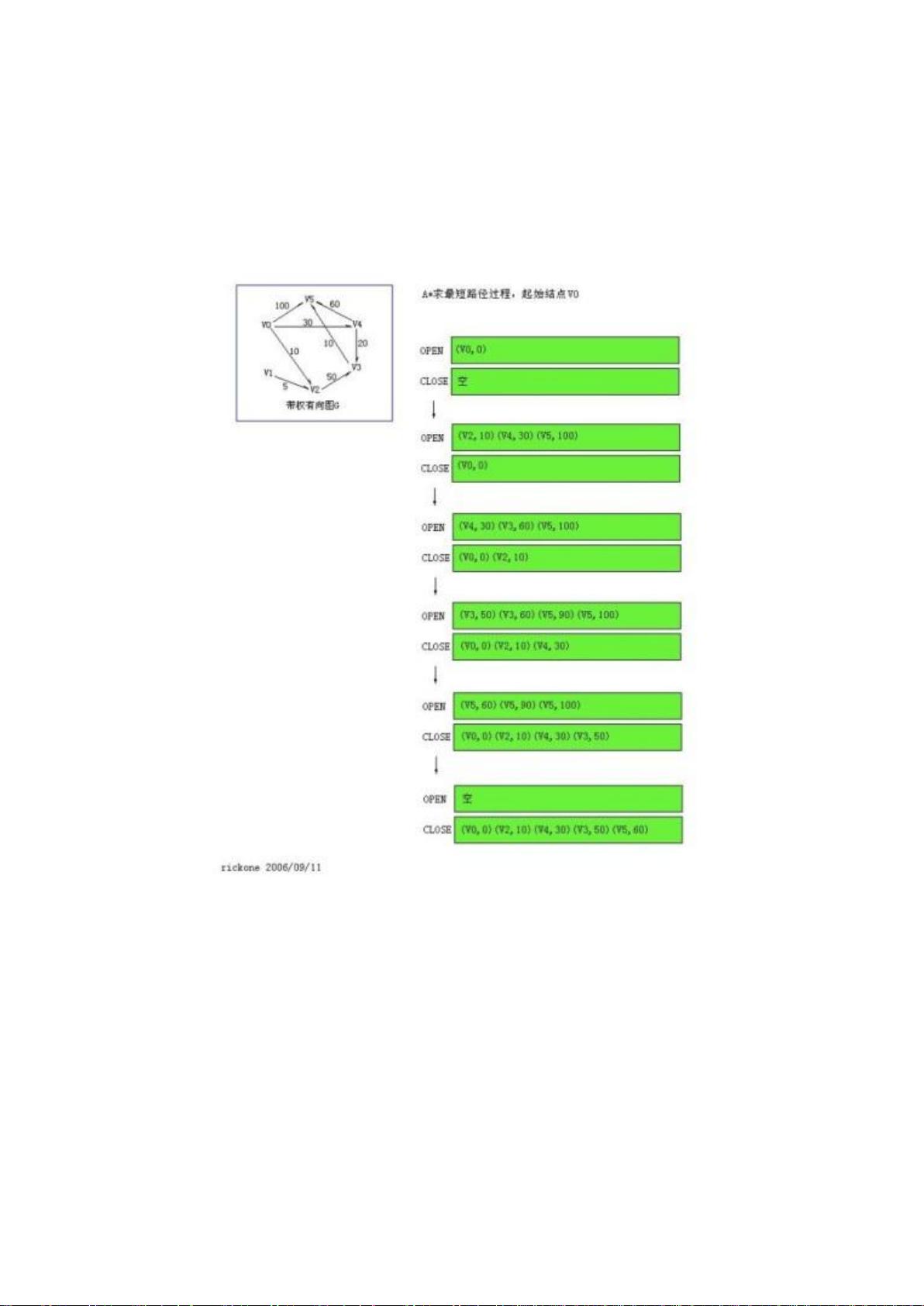
在IT领域，算法是解决问题和优化计算过程的关键工具。"十五个经典算法研究与总结"这份资料涵盖了数据结构和算法的精华，对于学习和提升编程技能具有重要意义。下面，我们将详细探讨这些经典算法。 1. **红黑树**：红黑树是一种自平衡二叉查找树，它保证了任何节点到其每个叶子节点的所有路径都包含相同数量的黑色节点。这种特性使得红黑树在插入、删除和查找操作上都能保持较优的时间复杂度，通常为O(log n)。 2. **排序算法**：排序是计算机科学的基础，包括快速排序、归并排序、堆排序、冒泡排序、选择排序等。快速排序以其平均时间复杂度O(n log n)而著名，而归并排序则在最坏情况下也能保持O(n log n)。堆排序利用了堆的数据结构，能在原地进行排序。冒泡排序和选择排序虽然效率相对较低，但在特定场景下仍有其价值。 3. **SIFT（尺度不变特征变换）算法**：SIFT是一种用于图像处理的特征检测算法，能识别不同尺度和旋转的图像特征。它通过降维和关键点定位，使得图像在尺度变化、旋转、光照变化等条件下仍能稳定匹配。 4. **Dijkstra算法**：Dijkstra算法用于寻找图中两点之间的最短路径，常用于路由算法和网络流量问题。它以贪心策略为基础，每次扩展最短距离的未访问节点。 5. **Kruskal's算法和Prim's算法**：这两种是最小生成树算法，用于寻找无向图中边权重之和最小的树形子集。Kruskal's算法基于边的排序，而Prim's算法则从一个顶点开始逐步添加边。 6. **DFS（深度优先搜索）和BFS（广度优先搜索）**：DFS常用于遍历或搜索树或图，沿着一条路径深入直到达到终点，再回溯寻找其他路径。BFS则先访问离起点近的节点，适合找最近的邻居。 7. **动态规划**：动态规划是一种解决最优化问题的方法，通过将问题分解为子问题并存储子问题的解来避免重复计算。经典的例子包括斐波那契数列、背包问题和最长公共子序列问题。 8. **图的最短路径算法**：除了Dijkstra算法，还有Floyd-Warshall算法，用于求解所有节点对间的最短路径，适合稠密图。 9. **贪心算法**：贪心算法在每一步选择局部最优解，期望全局最优。例如霍夫曼编码和活动选择问题。 10. **分治算法**：分治策略将大问题分解为小问题，如归并排序和快速排序就是典型的分治应用。 11. **回溯法**：在尝试所有可能解的过程中，遇到无效或不符合条件的解时，会回溯尝试其他分支。常用于八皇后问题、数独求解等。 12. **A*算法**：A*算法是启发式搜索算法，结合了Dijkstra算法和最佳优先搜索，引入了评估函数来引导搜索，提高效率。 13. **Bitwise操作**：位操作在计算机科学中广泛使用，用于高效地进行数据处理和节省内存。例如，位掩码用于高效地处理多个布尔值。 14. **Strassen矩阵乘法**：这是一种优化矩阵乘法的算法，通过分解和重组矩阵来减少运算次数，但实际应用中受限于其较高的空间复杂度。 15. **快速傅里叶变换(FFT)**：FFT是一种高效的计算离散傅里叶变换的算法，广泛应用于信号处理、图像分析等领域。 这些经典算法构成了计算机科学的基石，理解并掌握它们对于成为一名优秀的程序员至关重要。通过深入学习和实践，我们可以更好地解决实际问题，提高代码性能。