解:(1)信源序列中含有 3 个或小于 3 个“0”的各信源序列个数有:
01 23
100 100 100 100
CCCC=+++
=1+100+4950+161700=166750
对 M 个信源序列进行无失真的二元等长编码,必须:
17.35
2 166750 2
l
M≥= =
所以所需的码长的最小长度:
18l
(2)
4 96 4 5 95 5 99 99 100 100
100 0 1 100 0 1 100 0 1 100 1
PCPP CPP CPP CP=++++"
1 100 1 99 2 98 2 3 97 3
100 0 100 0 1 100 0 1 100 0 1
1 0.0017CP CPPCPP CPP=− − − − =
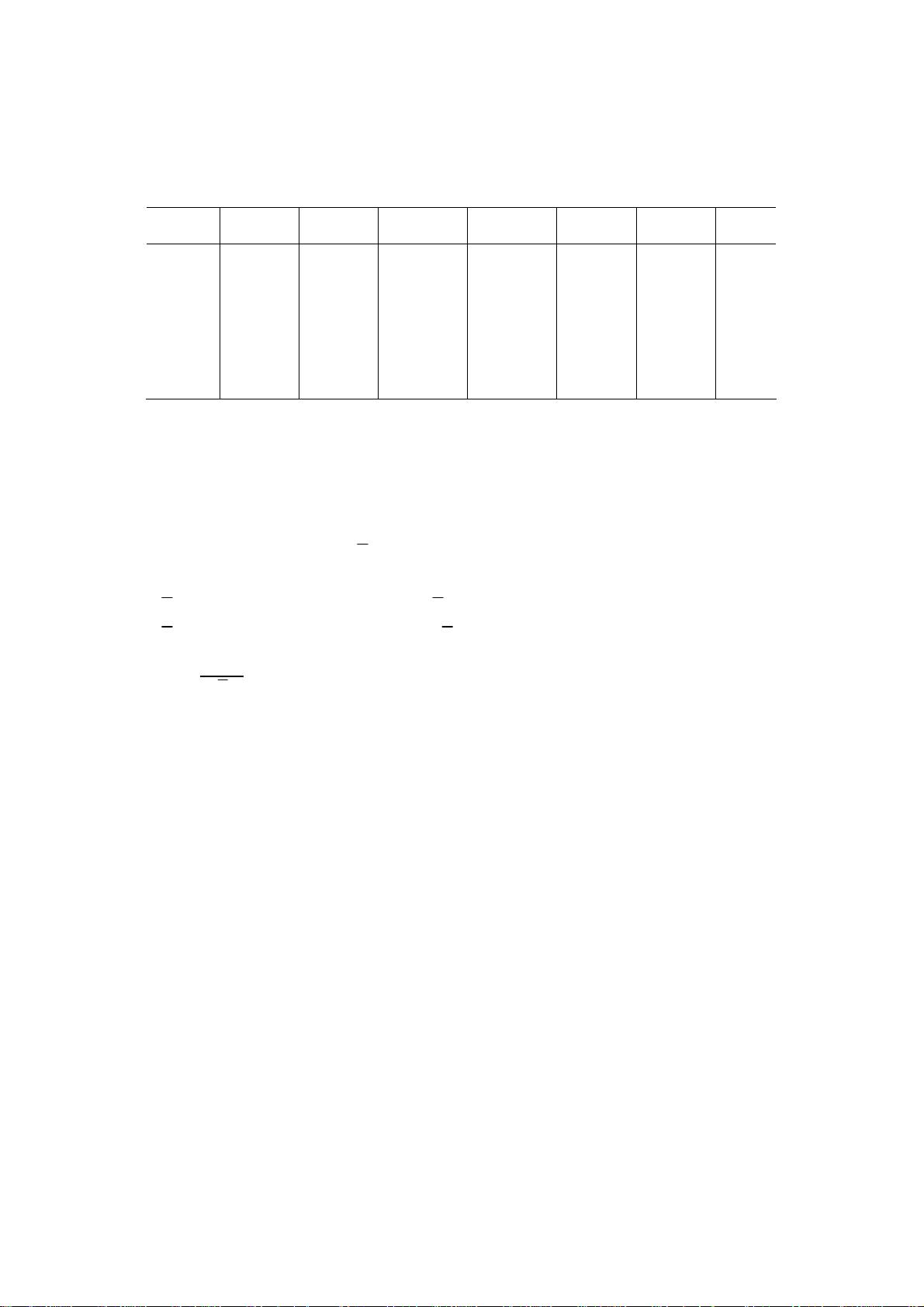
5.9 某信源有 6 个符号,概率分别为 3/8,1/6,l/8,l/8,1/8,1/12,试求三进码元(0,1,2)的费诺
码,并求出其编码效率。
解:
信源符号 概率 编码 码字 码长
X
1
3/8 0 0 1
X
2
1/6 0 10 2
X
3
1/8
1
1 11 2
X
4
1/8 0 20 2
X
5
1/8 1 21 2
X
6
1/12
2
2 22 2
H(X)=-((3/8)*log(3/8)+(1/6)*log(1/6)+(1/8)*log(1/8)+(1/8)*log(1/8)+(1/8)*log(1/8)+(1/12)*log(1/12))
=2.3852 (三进制单位/信源符号)
H
3
(X)= H(X)/ 1.5850=2.3852/1.5850= 1.5049(三进制单位/信源符号)
=(3/8)*1+ (1/6)*2+ (1/8)*2+ (1/8)*2+ (1/8)*2+ (1/12)*2=1.625(码符号/信源符号)
η= H
3
(X)/
=1.5049/1.625= 92.61 %
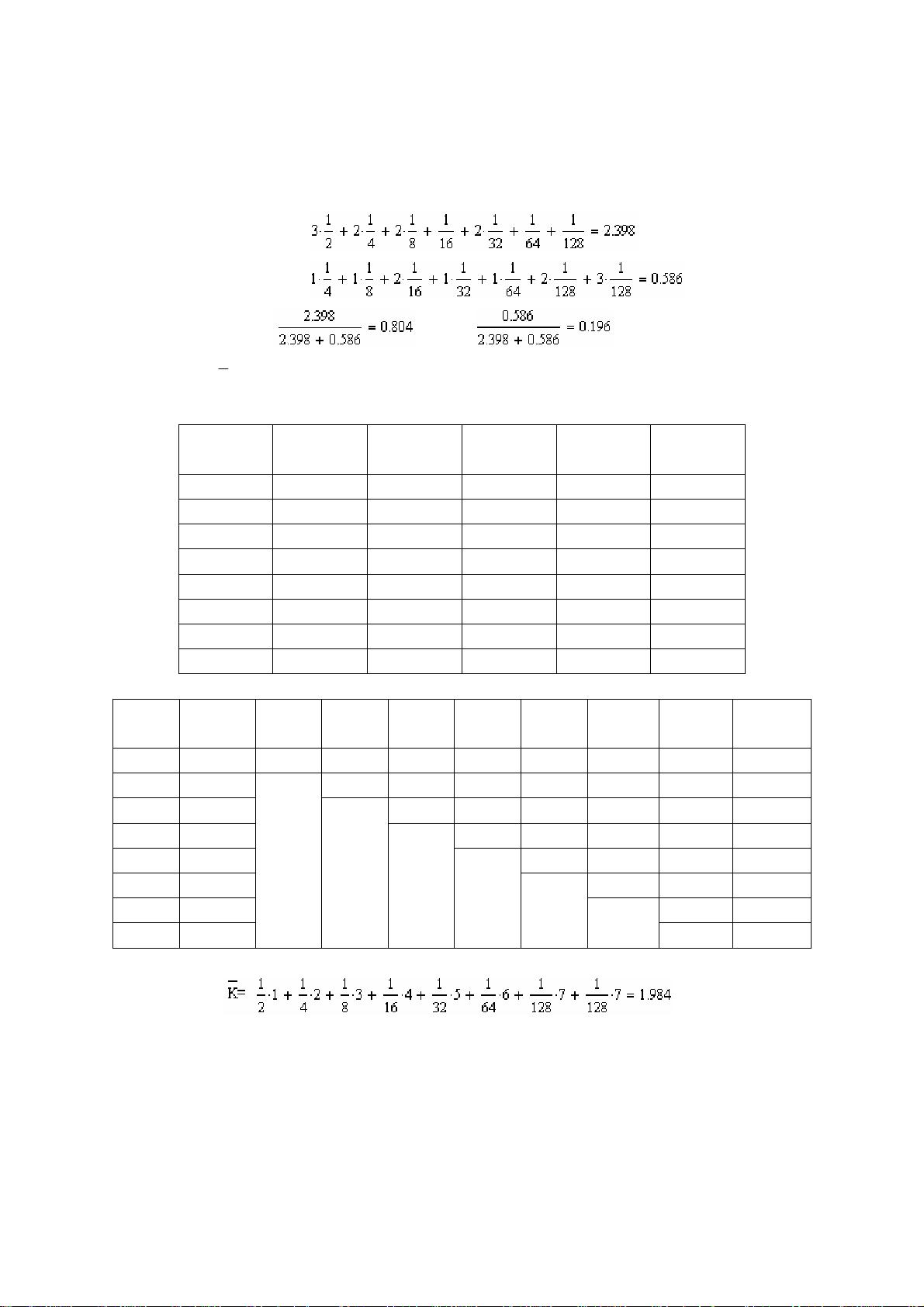
5.10 对下面给定的概率分布和基数,找出一个霍夫曼编码:
(1)
(0.2,0.1, 0.1, 0.3, 0.1, 0.2), ( ) 2;( ) 3;( ) 4;( ) 5.Parbrcr===dr==
解:(1)a、00 10 11 011 0100 0101
b、00 01 02 10 11 12
c、00 01 10 11 12 13
d、1 00 01 02 03 04
5.14 信源符号 X 有 7 种字母,概率为 0.32,0.22,0.18,0.16,0.08,0.04。
(1) 求符号熵 H(X);(2) 用香农编码法编成二进制变长码,计算其编码效率;
(3) 用费诺编码法编成二进制变长码,计算其编码效率;
(4) 用霍夫曼编码法编成二进制变长码,计算其编码效率;
(5) 用霍夫曼编码法编成三进制变长码,计算其编码效率;
(6) 若用逐个信源符号来编定长二进制码,要求不出差错译码,求所需要的每符号的平均信息
率和编码效率。
解:(
1
)信源熵
H(X)=-(0.32*log0.32+0.22*log0.22+0.18*log0.18+0.16*log0.16+0.08*log0.08+0.04*log0.04
= 2.352
(比特
/
信源符号)